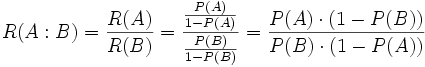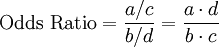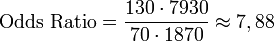Odds Ratio

Das Quotenverhältnis, auch Odds Ratio, Odds-Verhältnis, Kreuzproduktverhältnis oder Chancenverhältnis genannt, ist eine statistische Maßzahl, die etwas über die Stärke eines Zusammenhangs von zwei Merkmalen aussagt. Es ist damit ein Assoziationsmaß^[1], bei dem zwei Odds miteinander verglichen werden.^[2]

Berechnung

Das Quotenverhältnis (oder Odds Ratio) wird so berechnet:

$R(A:B) = {R(A) \over R(B)} = {{P(A) \over {1-P(A)}} \over {P(B) \over {1-P(B)}}} = {{P(A) \cdot (1-P(B))} \over {P(B) \cdot (1-P(A))}}$

mit R(A) = Odds(A).

Interpretation

Ein Quotenverhältnis von

• genau 1 bedeutet, dass es keinen Unterschied in den Odds gibt,
• >1 bedeutet, dass die Odds der ersten Gruppe größer sind,
• <1 bedeutet, dass die Odds der ersten Gruppe kleiner sind.

Anwendung

Das Quotenverhältnis wird häufig in Epidemiologie und Medizin verwendet, um zu erfahren, wie stark ein vermuteter Risikofaktor mit einer bestimmten Erkrankung zusammenhängt. Der Vorteil von Odds Ratios gegenüber Risk Ratios ist, dass man es bei allen Studiendesigns anwenden kann, also sowohl bei Fall-Kontroll-Studien, als auch bei Querschnitt- und Interventionsstudien.

Typischerweise vergleicht man dabei Personen mit einem potentiellen Risikofaktor für eine Erkrankung mit Personen ohne diesen Risikofaktor bzgl. des Auftretens ebenjener Erkrankung. Die gewonnenen Daten werden in einer Kreuztabelle dargestellt, die es auch leicht macht, die Odds Ratio direkt zu errechnen:

Anzahl der Personen …

	mit Risikofaktor	ohne Risikofaktor
erkrankt	a	b
nicht erkrankt	c	d

Es gilt dann:

$\mathrm{Odds\ Ratio}=\frac {a/c}{b/d} = \frac {a \cdot d}{b \cdot c}$

Das Quotenverhältnis (Odds Ratio) ist ein Maß dafür, um wie viel größer die Chance zu erkranken (im Sinne einer Quote) in der Gruppe mit Risikofaktor ist, verglichen mit der Gruppe ohne Risikofaktor. Das Quotenverhältnis nimmt Werte zwischen 0 und Unendlich an. Ein Wert von 1 bedeutet ein gleiches Quotenverhältnis.

Ein Beispiel mit fiktiven Daten

Angenommen man möchte den Zusammenhang zwischen dem Auftreten von Herzinfarkten und Rauchen untersuchen. Man beobachtet 10.000 Patienten und stellt fest, ob sie rauchen oder nicht und ob sie schon einmal einen Herzinfarkt erlitten haben. Es ergibt sich folgende Kreuztabelle:

Anzahl der Personen …

	die rauchen	die nicht rauchen
mit Herzinfarkt	130	70
ohne Herzinfarkt	1870	7930

Von 2000 Personen die rauchen, haben also 130 einen Herzinfarkt erlitten. Es ergibt sich das Quotenverhältnis

$\mathrm{Odds\ Ratio}=\frac {130 \cdot 7930}{70 \cdot 1870} \approx 7,88$

Unterschied zum Relativen Risiko

Anders als das relative Risiko bezieht sich das Quotenverhältnis auf Quoten und nicht auf Wahrscheinlichkeiten.

Folgendes Beispiel soll den Unterschied zwischen Quotenverhältnis und relativem Risiko erläutern:

Depression

Geschlecht	ja	nein
weiblich	40	143
männlich	10	101

Die Depression mit den Kategorien "ja" und "nein" ist die Risikovariable, das Geschlecht mit den Kategorien "weiblich" und "männlich" die unabhängige (ursächliche) Variable.

Bei den Frauen beträgt die Inzidenzrate: $40:(40+143)=0,219\,$

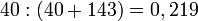
Bei den Männern beträgt die Inzidenzrate: $10:(10+101)=0,09\,$

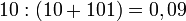
Das relative Risiko ist nun der Quotient aus beiden Inzidenzraten: $0,219:0,090=2,426\,$

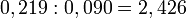
Das Quotenverhältnis hingegen berechnet man folgendermaßen:

$(40 \cdot 101):(143 \cdot 10)=2,825\,$.

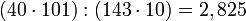Wie man sieht, kommt man zu unterschiedlichen Ergebnissen.^[3]

Assoziationsmaß nach Yule

Alternativ kann man das von George Udney Yule (1871-1951) vorgeschlagene Assoziationsmaß Q (Yules Q) verwenden, das sich als eine Transformation des Quotenverhältnisses darstellen lässt (Q = (OR − 1) / (OR + 1)) und das Quotenverhältnis auf das Intervall zwischen − 1 und + 1 normiert, mit dem Wert Q = 0, wenn beide Variablen statistisch voneinander unabhängig sind.

Einzelnachweise

1. ↑ Kapitel Kreuzproduktverhältnis (Odds Ratio) im Glossar zur Datenerhebung und statistischen Analyse (abgerufen am 6. Januar 2008)
2. ↑ Es scheint sinnvoll, als Begriff "Quotenverhältnis" oder (englisch) "Odds Ratio" oder (gemischt) "Odds-Verhältnis" zu verwenden, weil das "Chancenverhältnis" leicht mit dem "relativen Risiko" verwechselt werden kann, welches anders definiert ist. Der Begriff "Kreuzproduktverhältnis" ist insofern irreleitend, als dass er nichts mit dem Kreuzprodukt der linearen Algebra zu tun hat.
3. ↑ Bühl, Achim; Zöfel, Peter (2005): SPSS 12 Pearson Studium; München