Orakelmaschine

Eine Orakel-Turingmaschine ist eine , die mit einem Orakel verbunden ist. Bildhaft kann man sich ein Orakel als eine black box vorstellen, die von der Turingmaschine befragt werden kann und ein Problem in einem Schritt löst. Der Begriff der Orakel-Turingmaschine dient in der dazu, von Berechenbarkeiten und Komplexitäten zu definieren und deren Eigenschaften zu studieren.

Durch geeignete Orakel kann man die verstärken oder die verringern. Zum Beispiel Turingmaschinen mit dem Halteproblem als Orakel können das für Turingmaschinen lösen. Turingmaschinen mit als Orakel können jedes Problem aus in polynomialer Zeit lösen. Orakel werden auch verwendet, um deterministisch zu modellieren. Eine nichtdeterministische Turingmaschine kann nämlich als Schar von deterministischen Orakel-Turingmaschinen wiedergegeben werden. Der Scharparameter, das Orakel, drückt dabei die Folge der nichtdeterministischen Entscheidungen aus.

Definition

Sei 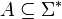$A\subseteq \Sigma^*$ eine über dem Alphabet . Eine Orakel-Turingmaschine mit Orakel A ist eine Turingmaschine M mit einem zusätzlichen Eingabeband (Orakelband) und drei ausgezeichneten Zuständen: q_j,q_n,q_?. Schreibt M ein 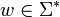$w\in\Sigma^*$ auf das Orakelband und geht in den Zustand q_? über, so befragt M das Orakel: Der Nachfolgezustand von q_? sei q_j falls 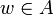$w\in A$ gilt und andernfalls q_n. Anschließend wird das Orakelband gelöscht.

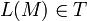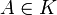Wenn T und K Klassen von Sprachen sind, dann bezeichnet T^K die Klasse der Sprachen, die von Turingmaschine M mit Orakel A akzeptiert werden, wobei $L(M)\in T$und $A\in K$ sind. Typische Klassen sind einelementige Klassen, wie P oder , oder auch die Klasse aller Sprachen.

Beispiele:

• P^SAT bezeichnet die Klasse der Sprachen, die von einer deterministischen, polynomiell zeitbeschränkten Turingmaschine mit Orakel SAT akzeptiert werden.
• NP^NP bezeichnet die Klasse der Sprachen, die von einer nichtdeterministischen, polynomiell zeitbeschränkten Turingmaschine mit Orakel aus der Klasse NP akzeptiert werden.

Diese Komplexitätsklassen werden unter anderem dazu genutzt, um die zu definieren.

Eigenschaften

• Für zwei Komplexitätsklassen T, K und eine Sprache 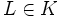$L \in K$ gilt T^K = T^L, falls folgende Bedingungen erfüllt sind:
  1. L ist K- bezüglich einer $\preceq$
  2. Die T zugrundeliegende Klasse von Turingmaschinen ist mächtig genug, die Reduktion $\preceq$ zu berechnen

     Beispielsweise gilt P^NP = P^SAT, da SAT NP-vollständig bezüglich ist.

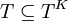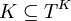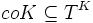• Jede Orakel-Turingmaschine hat mindestens die Fähigkeiten seiner Turingmaschine, seines Orakels und der Komplementsprache seines Orakels. Es gilt daher $T \subseteq T^K$, $K \subseteq T^K$ und $coK \subseteq T^K$ für alle Klassen T und K. Letztere Eigenschaft ergibt sich, wenn man die Zustände q_j und q_n vertauscht interpretiert. Insbesondere gilt also T^K = T^coK

• Für jede mittels deterministischer Turingmaschine definierte Komplexitätsklasse K und jede Oberklasse 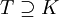$T \supseteq K$ gilt stets T^K = T, denn anstatt das Orakel zu befragen, kann eine Turingmaschine die Antwort selbst berechnen. Auf diese Weise zeigt man z.B. P^P = P und NP^P = NP. Die Aussage lässt sich nicht auf nichtdeterministische Komplexitätsklassen verallgemeinern. Grund dafür ist die notwendige Eigenschaft K = coK der Orakelklasse K. Beispielsweise würde aus NP^NP = NP die bisweilen ungeklärte Beziehung coNP = NP folgen $(\overline{SAT} \in NP)$.

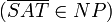Zum Halteproblem

Man beachte, dass das Orakel in keiner Weise beschränkt ist. Auch Sprachen, die nicht sind, kommen als Orakel in Frage. Also kann man zum Beispiel das Halteproblem als Orakel verwenden. Solche Halteorakel-Turingmaschinen können offensichtlich das von Turingmaschinen (ohne Orakel) lösen. Das steht natürlich nicht im Widerspruch zum Unentscheidbarkeitresultat des Halteproblems, denn dieses besagt ja nur, dass es keine Turingmaschine ohne Orakel gibt, die das Problem löst. Allerdings ist auch das Halteproblem von Halteorakel-Turingmaschinen nicht durch Halteorakel-Turingmaschinen lösbar.

Die Konstruktion von immer stärkeren Orakel-Turingmaschinen führt zur .

Literatur

• Jeffrey D. Ullman: Einführung in die Automatentheorie, Formale Sprachen und Komplexitätstheorie. Oldenbourg, München/Wien 2000, ISBN 3486254952. 
• Christos Papadimitriou: Computational Complexity. Addison-Wesley, 1994.