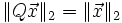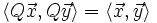- Orthogonalmatrix
-
Eine orthogonale Matrix ist in der linearen Algebra eine quadratische, reelle Matrix, deren Zeilen- und Spaltenvektoren paarweise orthonormal zueinander sind. Sie stellen Kongruenzabbildungen, also Spiegelungen und Drehungen, dar. Der analoge Begriff bei komplexen Matrizen ist die unitäre Matrix.
Damit gilt, dass die Transponierte einer orthogonalen Matrix gleichzeitig ihre Inverse ist. Zur Lösung eines quadratischen linearen Gleichungssystems mit orthogonaler Koeffizientenmatrix muss diese also nur transponiert und anschließend eine Matrizenmultiplikation durchgeführt werden.
Inhaltsverzeichnis
Definierende Eigenschaften
Gegeben sei eine quadratische Matrix
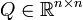 . Diese heißt orthogonal, wenn eine der folgenden äquivalenten Eigenschaften erfüllt ist:
. Diese heißt orthogonal, wenn eine der folgenden äquivalenten Eigenschaften erfüllt ist:- Die Spaltenvektoren bzw. die Zeilenvektoren von Q bilden eine Orthonormalbasis des
 , es gilt also QTQ = QQT = I.
, es gilt also QTQ = QQT = I. - Q ist invertierbar und ihre Transponierte ist gleichzeitig ihre Inverse:
- QT = Q − 1 .
- Durch eine Multiplikation mit Q ändert sich die euklidische Länge eines Vektors nicht (Längentreue):
- Die Multiplikation mit Q ist invariant gegenüber der Bildung des euklidischen Skalarprodukts zweier Vektoren (Winkeltreue):
Weitere Eigenschaften
- QT ist ebenfalls eine orthogonale Matrix.
- Das Produkt zweier orthogonaler Matrizen ist wieder orthogonal.
- Eine orthogonale Matrix ist normal und damit über den komplexen Zahlen diagonalisierbar.
- Eine orthogonale Matrix erhält sowohl die euklidische als auch die Frobeniusnorm einer Matrix, sowie ihre Kondition in den beiden Normen.
Geometrische Entsprechung
Aufgrund der oben genannten Längen- und Winkeltreue stellen orthogonale Matrizen Kongruenzabbildungen dar. Damit ist der Betrag der Determinante einer orthogonalen Matrix Eins, für jeden Eigenwert
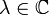 von Q gilt also
von Q gilt also 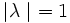 . Orthogonale Matrizen, deren Determinante 1 ist, entsprechen Drehungen, orthogonale Matrizen, deren Determinante − 1 ist, entsprechen in der Ebene Spiegelungen an einer Ursprungsgeraden und im Raum Ebenenspiegelungen oder Drehspiegelungen.
. Orthogonale Matrizen, deren Determinante 1 ist, entsprechen Drehungen, orthogonale Matrizen, deren Determinante − 1 ist, entsprechen in der Ebene Spiegelungen an einer Ursprungsgeraden und im Raum Ebenenspiegelungen oder Drehspiegelungen.Die orthogonale Gruppe
Alle orthogonalen Matrizen einer gegebenen Dimension n bilden die orthogonale Gruppe O(n). Die orthogonalen Matrizen, deren Determinante gleich 1 ist, bilden eine Untergruppe, die spezielle orthogonale Gruppe SO(n).
- Die Spaltenvektoren bzw. die Zeilenvektoren von Q bilden eine Orthonormalbasis des
Wikimedia Foundation.