P!=NP

Das P-NP-Problem (auch P≟NP, P versus NP) ist ein ungelöstes Problem der Mathematik und theoretischen Informatik, speziell der Komplexitätstheorie. Es stellt die Frage, ob Probleme existieren, für die eine gegebene Lösung leicht überprüft werden kann, das Finden einer solchen Lösung jedoch extrem schwierig ist. Dies ist formal äquivalent zu der Frage, in welcher Beziehung die beiden Komplexitätsklassen P und NP stehen. Erkannt wurde das Problem zu Beginn der 1970er Jahre aufgrund unabhängig voneinander erfolgter Arbeiten von Stephen Cook und Leonid Levin.

Das P-NP-Problem gilt als eines der wichtigsten offenen Probleme der Informatik und wurde vom Clay Mathematics Institute in die Liste der Millennium-Probleme aufgenommen.

P und NP

Die Komplexitätsklasse NP, unter der Annahme P≠NP. In diesem Fall enthält NP auch Probleme oberhalb von P, die nicht NP-vollständig sind.^[1]

Die Komplexitätstheorie klassifiziert Probleme, die von Computern berechnet werden können, anhand des zu ihrer Lösung erforderlichen Aufwands. Eine Möglichkeit zur Quantifizierung des Berechnungsaufwands ist die Zahl der maximal notwendigen Rechenschritte, die Zeitkomplexität. Die Komplexität eines Problems wird hierbei immer im Verhältnis zur Länge der Eingabe für die Berechnung angegeben. Zur exakten Analyse der Zeitkomplexität werden außerdem formale Maschinenmodelle benötigt. Ein häufig verwendetes Modell ist dabei die deterministische Turingmaschine, welche als die Abstraktion eines realen Computers angesehen werden kann.

Eine der komplexitätstheoretischen Problemkategorien ist die Komplexitätsklasse P. Bei Lösung durch eine deterministische Turingmaschine kann für jedes Problem dieser Klasse ein Polynom der Form n^k angegeben werden, das die Zeitkomplexität im Verhältnis zur Eingabelänge n nach oben beschränkt. Probleme aus P sind somit deterministisch in Polynomialzeit lösbar.

P wird gelegentlich als Klasse der praktisch lösbaren Probleme bezeichnet. Falls zu einem bestimmten Zeitpunkt die maximale Eingabelänge, für die ein Problem in akzeptabler Zeit gelöst werden kann, bei n liegt, wird hier die 2^k-fache Rechenleistung benötigt, um das Problem bei doppelter Eingabelänge in entsprechender Zeit zu lösen. Sofern das Mooresche Gesetz vorausgesetzt wird, entspräche dies etwa 2*k Jahren Hardwareentwicklung. Obwohl dieser grobe Richtwert aus verschiedenen Gründen noch zu optimistisch gewählt ist, zeigt er, dass die Lösbarkeit von Problemen in P durch Fortschritte in der Computertechnologie positiv beeinflusst werden kann.

Beispiele für Probleme der Komplexitätsklasse P sind das Sortierproblem oder das Schaltkreis-Auswertungsproblem.

Eine weitere anhand der deterministischen Turingmaschine definierte Problemmenge ist die Komplexitätsklasse EXP. Anstelle eines Polynoms wird hier als obere Schranke für die Zeitkomplexität eine Funktion der Form 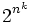$2^{n^k}$ in Abhängigkeit von der Eingabelänge n angegeben. Die Lösung der schwersten Probleme dieser Klasse benötigt also exponentielle Zeit. Weiterhin ist die Klasse P vollständig in EXP enthalten. Für einige Probleme in EXP kann jedoch gezeigt werden, dass diese nicht in Polynomialzeit gelöst werden können, z.B. die Frage, ob eine Turingmaschine der Größe n auf einer Eingabe der Größe n innerhalb von 2ⁿ Schritten anhält oder nicht. Die Lösbarkeit dieser Probleme kann nach derzeitigem Stand des Wissens auch durch zukünftige technologische Fortschritte nicht wesentlich verbessert werden.

Die Komplexitätstheorie definiert jedoch noch weitere Maschinenmodelle neben der deterministischen Turingmaschine. Ein wichtiges Modell ist die nichtdeterministische Turingmaschine, welche eine Erweiterung der deterministischen Variante darstellt. Eine nichtdeterministische Turingmaschine hat zu jedem Zeitpunkt eventuell mehrere Möglichkeiten, ihre Berechnung fortzusetzen, der Rechenweg ist deshalb nicht eindeutig bestimmbar. Es handelt sich dabei um ein theoretisches Modell, das nicht gleichwertig zu realen Computern ist. Sein Nutzen ist in diesem Zusammenhang, dass durch nichtdeterministische Turingmaschinen eine weitere Komplexitätsklasse unterschieden werden kann, welche innerhalb von EXP liegt und ihrerseits P einschließt.

Die Komplexitätsklasse NP ist die Menge aller von nichtdeterministischen Turingmaschinen in Polynomialzeit lösbaren Probleme. Diese Teilmenge von EXP enthält eine sehr große Zahl relevanter Problemstellungen. Da sich die Probleme aus P natürlich auch nichtdeterministisch in Polynomialzeit lösen lassen, ist P eine Teilmenge von NP. Unklar ist aber, ob die beiden Klassen identisch sind, und damit auch, ob die schwersten Probleme der Klasse NP ebenso effizient wie die der Komplexitätsklasse P gelöst werden können.

Ein anschauliches Problem aus NP, für das nicht klar ist, ob es in P enthalten ist, ist das Rucksackproblem. Bei diesem Problem soll ein beliebig großer Behälter so mit vorgegebenen Gegenständen gefüllt werden, dass der Behälter maximal gefüllt und der Inhalt so wertvoll wie nur möglich ist. Ein anderes wichtiges Beispiel ist das Erfüllbarkeitsproblem der Aussagenlogik.

Lösung des Problems

Bisher existieren zum exakten Lösen von NP-vollständigen Problemen nur Exponentialzeitalgorithmen auf deterministischen Rechenmaschinen. Andere Klassen von Problemen, welche garantiert mindestens exponentielle Laufzeit benötigen, veranschaulichen die derzeit praktische Unlösbarkeit von NP-vollständigen Problemen (zum Beispiel Türme von Hanoi).

Im Gegensatz zu diesen Problemen, die oberhalb der Klasse NP liegen, ist für NP-vollständige Probleme wegen des offenen P-NP-Problems nicht bewiesen, dass ein optimaler Algorithmus exponentielle Laufzeit benötigt. Würde man für eines dieser Probleme einen auf deterministischen Rechenmaschinen polynomiell zeitbeschränkten Algorithmus finden, so könnte jedes beliebige Problem aus NP durch Polynomialzeitreduktion darauf reduziert und somit in deterministischer Polynomialzeit gelöst werden; in diesem Falle wäre also P = NP.

Da es bisher nicht gelungen ist, einen solchen Algorithmus zu entwerfen, vermutet der Großteil der Fachwelt, dass P≠NP gilt. Dies könnte mathematisch dadurch nachgewiesen werden, dass für ein Problem aus der Klasse NP bewiesen wird, dass kein deterministischer Polynomialzeitalgorithmus zu dessen Lösung existiert.

Relativierende Beweistechniken

Ein Beweis für die Beziehung zweier Komplexitätsklassen ist relativierend, wenn die Beziehung für beliebig hinzugefügte Orakel erhalten bleibt. Unter die Klasse der relativierenden Beweistechniken fällt z.B. auch das in der Komplexitätstheorie häufig eingesetzte Verfahren der Diagonalisierung. Zeigt man beispielsweise 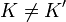$K \neq K'$ mittels Diagonalisierung, so gilt automatisch 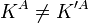$K^A \neq K'^A$ für jedes Orakel A. Der folgende wichtige Satz von T. Baker, J. Gill und R. Solovay ^[2] beweist, dass relativierende Beweistechniken kein probates Mittel für das P-NP-Problem sein können und viele Angriffsmethoden auf das P-NP-Problem aus der theoretischen Informatik hierdurch ausfallen:

Es existieren zwei Orakel A und B, so dass 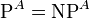$\operatorname{P}^A = \operatorname{NP}^A$ und $\operatorname{P}^B \neq \operatorname{NP}^B$.

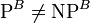Praktische Relevanz

Sehr viele, auch praktisch relevante Probleme, sind NP-vollständig. Die Lösung des Problems könnte daher von großer Bedeutung sein. Der Beweis von P=NP würde bedeuten, dass für Probleme der bisherigen Klasse NP Algorithmen existieren, die eine Lösung in – wesentlich schnellerer – Polynomialzeit generieren können. Da es jedoch in den vergangenen Jahrhunderten noch nicht gelungen ist, auch nur einen einzigen dieser Algorithmen zu finden, ist es zweifelhaft, dass nach dem Existenzbeweis umgehend ein Polynomialzeit-Algorithmus für diese Probleme gefunden würde.

Viele praktische Anwendungen für NP-vollständige Probleme, wie zum Beispiel das Problem des Handlungsreisenden, das Rucksackproblem oder das Problem der Färbung von Graphen, wären im Fall P=NP theoretisch optimal in kurzer Zeit lösbar.

Mit dem Beweis von P≠NP wären NP-Probleme endgültig als schwer lösbar klassifiziert. P≠NP entspricht derzeit der Annahme der meisten Wissenschaftler, und der Beweis wäre weniger folgenschwer als der Beweis von P=NP.

In der Kryptologie ist Komplexität im Gegensatz zu den meisten anderen Bereichen eine erwünschte Eigenschaft. Die Sicherheit von asymmetrischen Verschlüsselungsverfahren basiert allein auf diesem Faktor. Entgegen verbreiteten Fehleinschätzungen ist das P-NP-Problem dennoch kryptologisch eher unbedeutend. Diese beruhen auf verschiedenen komplexitätstheoretischen Definitionen, die zur Beurteilung der Sicherheit von Kryptosystemen nicht sinnvoll sind. Problematisch sind in diesem Zusammenhang insbesondere die formale Definition einer Einwegfunktion sowie die übliche Betrachtung des schlechtesten Falls (Worst Case) als Maß der Komplexität.

Siehe auch

• Karps 21 NP-vollständige Probleme
• Parametrisierte Algorithmen

Quellen

1. ↑ R. E. Ladner: On the structure of polynomial time reducibility, J.ACM, 22, pp. 151–171, 1975. Corollary 1.1. ACM Eintrag.
2. ↑ T. Bakerm, J. Gill, R. Solovay: Relativizations of the P=?NP question., SIAM Journal on Computing 4, pp. 431–442, 1975

Weblinks

• Vorlesungsreihe zur "Komplexitätstheorie", Prof. Dr. Christoph Meinel, Hasso-Plattner-Institut (Sommersemester 2008)
• Clay Mathematics Institute: P vs NP Problem (englisch)
• „The P-versus-NP page“: Eine Sammlung von Links zu wissenschaftlichen Artikeln zum P-NP-Problem (englisch)