P-Gruppe

Für eine Primzahl p ist eine p-Gruppe in der Gruppentheorie eine Gruppe, in der die Ordnung jedes Elements eine Potenz von p ist. Das heißt, für jedes Element g der Gruppe gibt es eine natürliche Zahl n, so dass g hoch pⁿ gleich dem neutralen Element der Gruppe ist.

Eine endliche p-Gruppe ist einfach eine Gruppe von Primzahlpotenzordnung.

Die Sylow-Sätze ermöglichen es, p-Untergruppen von endlichen Gruppen mit kombinatorischen Methoden aufzufinden. Besonders wichtig sind dabei die maximalen p-Untergruppen, die Sylowgruppen einer endlichen Gruppe.

Eigenschaften

• Eine Untergruppe H einer Gruppe G heißt p-Untergruppe, wenn sie eine p-Gruppe ist.
• Eine p-Untergruppe H einer Gruppe G heißt p-Sylowuntergruppe oder p-Sylowgruppe von G, wenn sie maximale p-Untergruppe von G ist. Das heißt, für jede p-Untergruppe U von G folgt aus 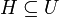$H \subseteq U$, dass H = U gilt. (Dabei steht p hier für eine feste Primzahl.)

Beispiele

Sei p stets eine Primzahl.

Beispiele endlicher p-Gruppen:

• Die zyklische Gruppe C_p ist eine abelsche p-Gruppe.

• Das direkte Produkt C_p × C_p ist eine abelsche p-Gruppe (nicht isomorph zu C_p²).

• Die Diedergruppe D₈ ist eine nichtabelsche 2-Gruppe.

Keine p-Gruppe ist z.B. die zyklische Gruppe C₆, da sie Elemente der Ordnung 6 enthält, und 6 ist keine Primzahlpotenz.

Ebenso ist die symmetrische Gruppe S₃ keine p-Gruppe, da sie Elemente der Ordnung 2 und Elemente der Ordnung 3 enthält, und diese Ordnungen nicht Potenzen derselben Primzahl sind.

Beispiel einer unendlichen p-Gruppe: Betrachte die Menge aller rationalen Zahlen, deren Nenner 1 oder eine Potenz der Primzahl p ist. Mit der Addition dieser Zahlen modulo 1 erhalten wir eine unendliche abelsche p-Gruppe.

Jede Gruppe, die zu G isomorph ist, heißt p^∞-Gruppe. Gruppen dieses Typs sind wichtig bei der Klassifikation unendlicher abelscher Gruppen.

Die p^∞-Gruppe kann auch beschrieben werden als die multiplikative Gruppe derjenigen komplexen Einheitswurzeln, deren Ordnung eine p-Potenz ist.

Weitere Eigenschaften

p-Gruppen sind spezielle Torsionsgruppen (dies sind Gruppen, in denen jedes Element endliche Ordnung hat).

Endliche p-Gruppen

Ist G eine endliche Gruppe, dann ist sie genau dann eine p-Gruppe, wenn ihre Ordnung (die Anzahl ihrer Elemente) selbst eine p-Potenz ist.

Das Zentrum einer endlichen p-Gruppe besteht nicht nur aus dem neutralen Element. Das zeigt man mit der Bahnenformel für die Konjugation.

Im Spezialfall einer Gruppe der Ordnung p² kann man sogar noch mehr sagen: In diesem Fall ist die Gruppe abelsch. Man zeigt das, indem man allgemeiner beweist, dass die Faktorgruppe G/Z(G) der Gruppe modulo dem Zentrum nur dann eine zyklische Gruppe ist, wenn sie die triviale (einelementige) Gruppe {e} ist.

Jede endliche p-Gruppe ist nilpotent und auflösbar.

p-Gruppen derselben Ordnung müssen nicht isomorph sein, z.B. sind die zyklische Gruppe C₄ und die Kleinsche Vierergruppe beides 2-Gruppen der Ordnung 4, aber nicht zueinander isomorph. Eine p-Gruppe muss auch nicht abelsch sein, z.B. ist die Diedergruppe D₈ eine nichtabelsche 2-Gruppe.

Jede nichttriviale endliche Gruppe enthält eine Untergruppe, die p-Gruppe ist. Details dazu sind im Artikel Sylow-Sätze beschrieben.