P-Vollständigkeit

In der Komplexitätstheorie ist P (auch: PTIME) diejenige Komplexitätsklasse, welche die Entscheidungsprobleme enthält, die in Polynomialzeit für deterministische Turingmaschinen lösbar sind. Diese Problemklasse wird allgemein als die Klasse der "praktisch lösbaren" Probleme betrachtet.

Eine Verallgemeinerung von P ist die Klasse NP. Die Probleme aus NP sind zwar ebenfalls in Polynomialzeit entscheidbar, jedoch wird hierfür ein nicht realisierbares, nämlich nichtdeterministisches Maschinenmodell eingesetzt. P ist sicher eine Teilmenge von NP. Es gehört jedoch zu den wichtigsten ungelösten Fragen der theoretischen Informatik, ob auch NP eine Teilmenge von P ist und somit, ob P=NP gilt (siehe auch P-NP-Problem).

Beziehung zu anderen Komplexitätsklassen

Die folgenden Beziehungen sind bekannt:

L ⊆ NL ⊆ LOGCFL ⊆NC ⊆ P ⊆ NP ⊆ PSPACE ⊆ EXPTIME ⊆ NEXPTIME

LOGCFL $\not=$ PSPACE

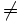P $\not=$ EXPTIME

P-Vollständigkeit

Ein Entscheidungsproblem A heißt P-vollständig genau dann, wenn es in der Komplexitätsklasse P liegt und wenn jedes Problem in P mit logarithmischem Platzverbrauch auf A reduziert werden kann, das heißt, wenn jede dieser Reduktionen in der Komplexitätsklasse L liegt (siehe auch: Vollständigkeit (Komplexitätstheorie)).

Ein bekanntes P-vollständiges Problem ist das Circuit-Value-Problem, bei dem bestimmt werden soll, ob das Ergebnis eines Booleschen Schaltkreises bei gegebener Eingabe einer gegebenen Ausgabe entspricht. Diese Probleme gehören zu den schwersten, noch effizient lösbaren Problemen aus der Komplexitätsklasse P. P-vollständige Probleme sind (momentan) schwer zu parallelisieren.

Bekannte Probleme in P

• PRIMES
• Lineare Programmierung

Weblinks

• P im Complexity Zoo (englisch)
• A Compendium of Problems Complete for P (englisch)