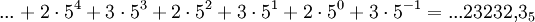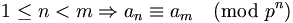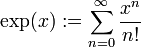- P-adischer Körper
-
Für jede Primzahl p bilden die p-adischen Zahlen einen Erweiterungskörper
 der rationalen Zahlen; sie wurden 1897 erstmals von Kurt Hensel beschrieben. Diese Körper werden benutzt, um Probleme in der Zahlentheorie zu lösen, oftmals unter Verwendung des lokal-global-Prinzips von Helmut Hasse, welches vereinfacht gesprochen aussagt, dass eine Gleichung genau dann über den rationalen Zahlen
der rationalen Zahlen; sie wurden 1897 erstmals von Kurt Hensel beschrieben. Diese Körper werden benutzt, um Probleme in der Zahlentheorie zu lösen, oftmals unter Verwendung des lokal-global-Prinzips von Helmut Hasse, welches vereinfacht gesprochen aussagt, dass eine Gleichung genau dann über den rationalen Zahlen  gelöst werden kann, wenn sie über den reellen Zahlen
gelöst werden kann, wenn sie über den reellen Zahlen  und allen
und allen  gelöst werden kann (was aber nicht so allgemein zutrifft, für die genaue Bedeutung siehe dort). Als metrischer Raum ist
gelöst werden kann (was aber nicht so allgemein zutrifft, für die genaue Bedeutung siehe dort). Als metrischer Raum ist  vollständig, und erlaubt so die Entwicklung einer p-adischen Analysis analog zur reellen Analysis.
vollständig, und erlaubt so die Entwicklung einer p-adischen Analysis analog zur reellen Analysis.Inhaltsverzeichnis
Motivation
Ist p eine fest gewählte Primzahl, dann kann jede ganze Zahl in einer p-adischen Entwicklung geschrieben werden (man sagt, die Zahl wird „zur Basis p geschrieben“, siehe auch Stellenwertsystem) der Form
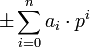 (1)
(1)
wobei die ai Zahlen aus {0,1,...,p − 1} sind. So ist etwa die 2-adische Entwicklung gerade die Binärdarstellung; zum Beispiel schreibt man
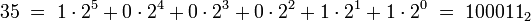 .
.
Die bekannte Verallgemeinerung dieser Beschreibung auf größere Zahlmengen (rationale und reelle) ist die Zulassung unendlicher Summen am unteren Ende, d.h. der folgenden Form:
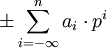 (2)
(2)
Diese Reihen sind konvergente Partialsummenfolgen bezüglich des gewöhnlichen Absolutbetrags. Zum Beispiel ist 0,13131313...5 die p-adische Darstellung von 1/3 zur Basis 5. In diesem System sind die ganzen Zahlen genau diejenigen, für die ai = 0 ist für alle i < 0.
Alternativ könnte man die Summen am anderen Ende ins Unendliche verlängern, und Reihen dieser Form erhalten:
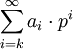 (3)
(3)
wobei k eine beliebige ganze Zahl ist. Auf diese Weise erhalten wir den Körper
 der p-adischen Zahlen. Diejenigen p-adischen Zahlen, für die ai = 0 für alle i < 0 ist, heißen p-adische ganze Zahlen. Analog zur gewöhnlichen p-adischen Entwicklung kann man diese Reihen als (nach links unendlich fortgesetzte) Ziffernfolge schreiben:
der p-adischen Zahlen. Diejenigen p-adischen Zahlen, für die ai = 0 für alle i < 0 ist, heißen p-adische ganze Zahlen. Analog zur gewöhnlichen p-adischen Entwicklung kann man diese Reihen als (nach links unendlich fortgesetzte) Ziffernfolge schreiben:Anschaulich besteht also die gewöhnliche p-adische Entwicklung aus Summen, die sich nach rechts fortsetzen mit immer kleineren (negativen) Potenzen von p, und die p-adischen Zahlen haben Entwicklungen, die sich nach links fortsetzen mit immer größeren p-Potenzen.
Mit diesen „formalen Laurentreihen in p“ kann man rechnen wie mit den gewöhnlichen p-adischen Entwicklungen reeller Zahlen: Addition von rechts nach links mit Übertrag, Multiplikation nach Schulmethode. Beachten muss man nur, dass sich Überträge ins Unendliche fortsetzen können, beispielsweise ergibt die Addition von ...444445 und 15 die Zahl 05. Das fehlende Vorzeichen ist also tatsächlich nicht nötig, da auch alle negativen Zahlen eine p-adische Darstellung haben. Damit lässt sich auch die Subtraktion nach Schulmethode von rechts nach links durchführen, unter Umständen mit einem unendlich oft auftretenden „Borgen“ (man versuche es bei 05-15=...44445). Die Division dagegen wird im Gegensatz zur Schulmethode auch von rechts nach links durchgeführt, dadurch wird das Ergebnis nach links fortgesetzt, falls die Division nicht „aufgeht“.
Ein technisches Problem ist nun, ob diese Reihen überhaupt sinnvoll sind, d.h. ob sie in irgendeinem Sinne konvergieren. Zwei Lösungen dafür werden nun vorgestellt.
Konstruktion
Analytische Konstruktion
Die reellen Zahlen können konstruiert werden als Vervollständigung der rationalen Zahlen. Sie werden dabei aufgefasst als Äquivalenzklassen von rationalen Cauchy-Folgen. Dies erlaubt uns zum Beispiel, die Zahl 1 als 1,000... zu schreiben, oder als 0,999... - es ist 1,000... = 0,999... in
 .
.Jedoch hängt bereits die Definition einer Cauchy-Folge von der verwendeten Metrik ab, und indem man statt der üblichen euklidischen Metrik, die vom Absolutbetrag erzeugt wird, eine andere Metrik benutzt, erhält man andere Vervollständigungen anstelle der reellen Zahlen.
p-adischer Betrag
Für eine fest vorgegebene Primzahl p definieren wir den p-adischen Betrag auf
 : Jede rationale Zahl x außer 0 lässt sich schreiben als x = pn(a / b) mit einer eindeutigen ganzen Zahl n und zwei ganzen Zahlen a, b, die beide nicht durch p teilbar sind. Wir setzen dann
: Jede rationale Zahl x außer 0 lässt sich schreiben als x = pn(a / b) mit einer eindeutigen ganzen Zahl n und zwei ganzen Zahlen a, b, die beide nicht durch p teilbar sind. Wir setzen dann 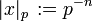 und
und 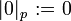 . Dies ist ein nichtarchimedischer Betrag.
. Dies ist ein nichtarchimedischer Betrag.Zum Beispiel ist
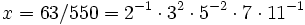 , damit ist
, damit ist- | x | 2 = 2, | x | 3 = 1 / 9, | x | 5 = 25, | x | 7 = 1 / 7, | x | 11 = 11
- | x | p = 1 für jede andere Primzahl p
Durch diese Definition des Betrags | x | p werden große Potenzen von p „betragsmäßig klein“. Mit diesem Betrag mit den p-adischen Zahlen wird ein diskreter Bewertungsring definiert.
p-adische Metrik
Die p-adische Metrik dp auf
 definiert man nun so: (Leutbecher, 1996, S. 118f)
definiert man nun so: (Leutbecher, 1996, S. 118f)- dp(x,y) = | x − y | p
Damit ist beispielsweise die Folge (1,5,52,53,54,...) in
 bezüglich der 5-adischen Metrik eine Nullfolge, wohingegen die Folge (1,1 / 2,1 / 4,1 / 8,...) beschränkt, aber keine Cauchy-Folge ist, denn für jedes n ist
bezüglich der 5-adischen Metrik eine Nullfolge, wohingegen die Folge (1,1 / 2,1 / 4,1 / 8,...) beschränkt, aber keine Cauchy-Folge ist, denn für jedes n ist- d5(1 / 2n,1 / 2n + 1) = | 1 / 2n + 1 | 5 = 1
Die Vervollständigung des metrischen Raums
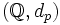 ist der metrische Raum
ist der metrische Raum  der p-adischen Zahlen; er besteht aus Äquivalenzklassen von Cauchy-Folgen, wobei zwei Cauchy-Folgen äquivalent heißen, wenn die Folge ihrer punktweisen p-adischen Abstände eine Nullfolge ist. Auf diese Weise erhalten wir einen vollständigen metrischen Raum, der (durch die wohldefinierten komponentenweisen Verknüpfungen der Cauchy-Folgen-Äquivalenzklassen) außerdem ein Körper ist, in dem
der p-adischen Zahlen; er besteht aus Äquivalenzklassen von Cauchy-Folgen, wobei zwei Cauchy-Folgen äquivalent heißen, wenn die Folge ihrer punktweisen p-adischen Abstände eine Nullfolge ist. Auf diese Weise erhalten wir einen vollständigen metrischen Raum, der (durch die wohldefinierten komponentenweisen Verknüpfungen der Cauchy-Folgen-Äquivalenzklassen) außerdem ein Körper ist, in dem  enthalten ist.
enthalten ist.Da die so definierte Metrik eine Ultrametrik ist, konvergieren Reihen bereits dann, wenn die Summanden eine Nullfolge bilden. In diesem Körper sind also die oben erwähnten Reihen der Form
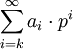 (3)
(3)
sofort als konvergent zu erkennen, falls k eine ganze Zahl ist und die ai in {0,1,...,p − 1} liegen. Man kann zeigen, dass sich jedes Element von
 als Grenzwert genau einer solchen Reihe darstellen lässt.
als Grenzwert genau einer solchen Reihe darstellen lässt.Algebraische Konstruktion
Hier wird zuerst der Ring der p-adischen ganzen Zahlen definiert, und danach dessen Quotientenkörper
 .
.Wir definieren
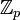 als projektiven Limes der Ringe
als projektiven Limes der Ringe 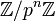 (siehe Restklassenkongruenz): Eine p-adische ganze Zahl ist dann eine Folge (an) von Restklassen an aus
(siehe Restklassenkongruenz): Eine p-adische ganze Zahl ist dann eine Folge (an) von Restklassen an aus 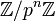 , wobei gilt:
, wobei gilt:Jede ganze Zahl m definiert eine Folge
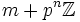 und kann daher als Element von
und kann daher als Element von 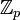 aufgefasst werden.(Leutbecher, 1996, S. 117f)
aufgefasst werden.(Leutbecher, 1996, S. 117f)Die komponentenweise definierte Addition und Multiplikation ist wohldefiniert, da Addition und Multiplikation ganzer Zahlen mit der Restklassenbildung vertauschbar ist. Damit hat jede p-adische ganze Zahl (an) die negative Zahl (pn − an), und jede Zahl deren erste Komponente a1 nicht 0 ist, hat ein Inverses, denn in dem Fall sind alle an zu pn teilerfremd, haben also ein Inverses bn modulo pn, und die Folge (bn) (welche die Kongruenzeigenschaft des projektiven Limes hat) ist dann die Inverse zu (an).
Jede p-adische Zahl kann auch als Reihe der oben beschriebenen Form (3) dargestellt werden, dabei sind die Partialsummen gerade die Komponenten der Folge. Zum Beispiel kann man die 3-adische Folge (2,8,8,35,35,35,...) auch schreiben als
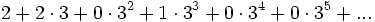 , oder in der verkürzten Schreibweise als ...0010223.
, oder in der verkürzten Schreibweise als ...0010223.Der Ring der p-adischen ganzen Zahlen ist nullteilerfrei, deshalb können wir den Quotientenkörper bilden und erhalten
 , den Körper der p-adischen Zahlen. Jedes von 0 verschiedene Element dieses Körpers kann man darstellen in der Form pnu, wobei n eine ganze Zahl ist, und u eine invertierbare p-adische ganze Zahl (also mit erster Komponente u1 ungleich 0). Diese Darstellung ist eindeutig.
, den Körper der p-adischen Zahlen. Jedes von 0 verschiedene Element dieses Körpers kann man darstellen in der Form pnu, wobei n eine ganze Zahl ist, und u eine invertierbare p-adische ganze Zahl (also mit erster Komponente u1 ungleich 0). Diese Darstellung ist eindeutig.Eigenschaften
Die Menge
 der p-adischen Zahlen ist überabzählbar.
der p-adischen Zahlen ist überabzählbar.Der Körper der p-adischen Zahlen enthält
 und hat deshalb Charakteristik 0. Dieser Körper kann nicht angeordnet werden.
und hat deshalb Charakteristik 0. Dieser Körper kann nicht angeordnet werden.Der topologische Raum
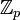 der p-adischen ganzen Zahlen ist ein kompakter Raum, der Raum aller p-adischen Zahlen ist lokal kompakt. Als metrische Räume sind beide vollständig.
der p-adischen ganzen Zahlen ist ein kompakter Raum, der Raum aller p-adischen Zahlen ist lokal kompakt. Als metrische Räume sind beide vollständig.Die Primelemente von
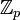 sind genau die zur Zahl p assoziierten Elemente. Dies sind auch genau die Elemente, deren Betrag gleich | p | = 1 / p ist; dieser Betrag ist der größte in
sind genau die zur Zahl p assoziierten Elemente. Dies sind auch genau die Elemente, deren Betrag gleich | p | = 1 / p ist; dieser Betrag ist der größte in  vorkommende Betrag, der kleiner ist als 1.
vorkommende Betrag, der kleiner ist als 1.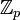 ist ein lokaler Ring, genauer ein diskreter Bewertungsring. Sein maximales Ideal wird von p (oder einem beliebigen anderen Primelement) erzeugt.
ist ein lokaler Ring, genauer ein diskreter Bewertungsring. Sein maximales Ideal wird von p (oder einem beliebigen anderen Primelement) erzeugt.Die reellen Zahlen haben nur eine einzige echte algebraische Erweiterung, die komplexen Zahlen; bereits der durch Adjunktion einer Quadratwurzel entstehende Erweiterungskörper ist algebraisch abgeschlossen. Im Gegensatz dazu hat der algebraische Abschluss von
 einen unendlichen Erweiterungsgrad.
einen unendlichen Erweiterungsgrad.  hat also unendlich viele inäquivalente algebraische Erweiterungen.
hat also unendlich viele inäquivalente algebraische Erweiterungen.Die Metrik auf
 lässt sich zu einer Metrik auf dem algebraischen Abschluss fortsetzen, allerdings ist diese dann nicht vollständig. Die Vervollständigung des algebraischen Abschlusses bezüglich dieser Metrik führt zum Körper
lässt sich zu einer Metrik auf dem algebraischen Abschluss fortsetzen, allerdings ist diese dann nicht vollständig. Die Vervollständigung des algebraischen Abschlusses bezüglich dieser Metrik führt zum Körper 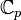 , der bezüglich seiner Analysis etwa den komplexen Zahlen entspricht.
, der bezüglich seiner Analysis etwa den komplexen Zahlen entspricht.Die übliche Definition der e-Funktion
konvergiert für alle x mit
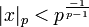 . Dieser Konvergenzkreis gilt für alle algebraischen Erweiterungen von
. Dieser Konvergenzkreis gilt für alle algebraischen Erweiterungen von  und deren Vervollständigungen, einschließlich
und deren Vervollständigungen, einschließlich 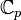 .
.Damit liegt exp(p) in
 für alle p > 2; in
für alle p > 2; in 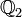 liegt exp(4). Es gibt algebraische Erweiterungen von
liegt exp(4). Es gibt algebraische Erweiterungen von  , in denen die p-te Wurzel von exp(p) bzw. die vierte Wurzel von exp(4) liegt; diese Wurzeln könnte man als p-adische Entsprechungen der Eulerschen Zahl auffassen. Diese Zahlen haben aber mit der reellen Eulerschen Zahl e = 2,718... wenig zu tun.
, in denen die p-te Wurzel von exp(p) bzw. die vierte Wurzel von exp(4) liegt; diese Wurzeln könnte man als p-adische Entsprechungen der Eulerschen Zahl auffassen. Diese Zahlen haben aber mit der reellen Eulerschen Zahl e = 2,718... wenig zu tun.Funktionen von
 nach
nach  mit Ableitung 0 sind konstant. Für Funktionen von
mit Ableitung 0 sind konstant. Für Funktionen von  nach
nach  gilt dieser Satz nicht; zum Beispiel hat die Funktion
gilt dieser Satz nicht; zum Beispiel hat die Funktion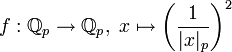 für
für 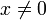 , f(0) = 0
, f(0) = 0
auf ganz
 die Ableitung 0, ist aber nicht einmal lokal konstant in 0. Dabei ist die Ableitung analog zum reellen Fall über den Grenzwert der Differenzenquotienten definiert, und die Ableitung in 0 ist
die Ableitung 0, ist aber nicht einmal lokal konstant in 0. Dabei ist die Ableitung analog zum reellen Fall über den Grenzwert der Differenzenquotienten definiert, und die Ableitung in 0 ist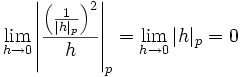 .
.
Sind
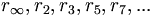 Elemente von
Elemente von 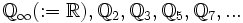 , dann gibt es eine Folge (xn) in
, dann gibt es eine Folge (xn) in  , so dass für alle p (einschließlich
, so dass für alle p (einschließlich  ) der Grenzwert der xn in
) der Grenzwert der xn in  rp ist. (Diese Aussage wird manchmal Näherungssatz genannt.)
rp ist. (Diese Aussage wird manchmal Näherungssatz genannt.)Quelle
- Armin Leutbecher: Zahlentheorie - Eine Einführung in die Algebra. Springer-Verlag, 1996, ISBN 3-540-58791-8, S. 116-130
Natürliche Zahlen
 | Ganze Zahlen
| Ganze Zahlen  | Rationale Zahlen
| Rationale Zahlen  | Reelle Zahlen
| Reelle Zahlen  | Komplexe Zahlen
| Komplexe Zahlen  | Quaternionen
| Quaternionen  | Oktaven
| Oktaven 
p-adische Zahlen
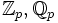
Wikimedia Foundation.