- Pandigitale Zahlen
-
Eine pandigitale Zahl (aus griechisch παν: „jedes“ und digital) ist eine dezimale ganze Zahl, die jede der zehn Ziffern von 0 bis 9 genau einmal enthält. Die erste Ziffer darf dabei nicht 0 sein.
Pandigitale Zahlen haben weder in der Mathematik noch in irgendeinem Anwendungsgebiet eine wirkliche Bedeutung. Sie werden zumeist als Kuriosität in mathematischen Rätseln nach Art der Lateinischen Quadrate oder der Sudokus verwendet.
Ein Beispiel ist die Zahl 1748592603.
Jede pandigitale Zahl hat die Quersumme 45 und ist damit durch 9 teilbar:
- 0 + 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45
Es gibt insgesamt 9 · 9! = 3265920 pandigitale Zahlen: Es gibt 9 Möglichkeiten für die erste Stelle (da die Null ausgeschlossen ist), 9 für die zweite (da die erste Ziffer ausgeschlossen ist), 8 für die dritte (die ersten beiden Ziffern dürfen nicht noch einmal verwendet werden), 7 für die vierte usw.
Die kleinsten pandigitalen Zahlen sind:
- 1023456789, 1023456798, 1023456879, 1023456897, 1023456978,
- 1023456987, 1023457689, 1023457698, 1023457869, 1023457896,
- 1023457968, 1023457986, 1023458679, 1023458697, 1023458769,
- 1023458796, 1023458967, 1023458976
Multidigital
Eine allgemeinere Definition von pandigitalen Zahlen ist die folgende: Eine Zahl oder ein mathematischer Ausdruck, der jede Ziffer zu einer Basis n genau einmal enthält. In Frankreich werden solche Zahlen auch multidigital genannt, die Zahlen zur Basis 10 decadigital.
Zur Basis 4 ist 1320 eine pandigitale Zahl und 2 + 1 = 3 + 0 eine pandigitale Summe.
Pandigitale Brüche
Pandigitale Brüche sind Brüche, die die Ziffern 1 bis 9 genau einmal enthalten.
Beispiele:
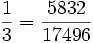 oder
oder 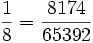
Weblinks
- Eric W. Weisstein: Pandigital Number auf MathWorld (englisch) (englisch)
- Eric W. Weisstein: Pandigital Fraction auf MathWorld (englisch) (englisch)
- Pandigitale-Zahlen-Generator
- Pandigital Fraction
Wikimedia Foundation.
