- Zahl
-
Dieser Artikel wurde auf der Qualitätssicherungsseite des Portals Mathematik eingetragen. Dies geschieht, um die Qualität der Artikel aus dem Themengebiet Mathematik auf ein akzeptables Niveau zu bringen. Bitte hilf mit, die Mängel dieses Artikels zu beseitigen, und beteilige dich bitte an der Diskussion!
Zahlen sind abstrakte mathematische Objekte, die u.a. Quantitäten (Anzahlen, Differenzen, Größenverhältnisse, ...) darstellen und unter anderem zum Zählen, Ordnen, Messen und Rechnen verwendet werden.
Inhaltsverzeichnis
Etymologie
Das deutsche Wort „Zahl“ entwickelte sich aus dem althochdeutschen Wort zala, welches „eingekerbtes Merkzeichen“ bedeutet. Eng verwandt sind die Begriffe zählen und Anzahl.
Aspekte des Begriffes Zahl
Kardinalzahl
Der kardinale Aspekt von Zahlen wird verwendet, wenn mit Zahlen eine Anzahl oder Quantität beschrieben wird.
- „Ich habe sechs Äpfel.“
- „Diese wiegen 1,8 Kilogramm.“ Mit einer Einheit wird hier eine physikalische Größe angegeben.
Ordinalzahl
Der ordinale Aspekt von Zahlen wird verwendet, wenn mit Zahlen eine Ordnung (Anordnung, Reihenfolge) beschrieben wird.
- „Er wohnt in Haus Nummer 14.“ Hier wird das gesuchte Haus nicht nur mit einer Nummer markiert, sondern es wird dabei auch eine Ordnung verwendet. Beim Suchen einer Adresse kann man die Tatsache verwenden, dass Häuser nach bestimmten Regeln nummeriert werden.
- „Beim Wettbewerb errang sie den dritten Platz.“
Die Kardinalzahlen sind durch ihre Mächtigkeit geordnet. Sie können als Ordinalzahl aufgefasst werden.
Darstellung von Zahlen
Seit Jahrtausenden haben sich in verschiedenen Kulturen für die Darstellung von Zahlen verschiedene Arten von Zahlzeichen entwickelt, die z.T. auf unterschiedliche Zahlensysteme zurückgreifen.
Das derzeit gebräuchlichste ist das Dezimalsystem mit den Ziffern 1, 2, 3, 4, 5, 6, 7, 8, 9 und 0.
Einige weitere Zahlensysteme werden heutzutage für spezielle technische oder wissenschaftliche Zwecke genutzt. Beispiele dafür sind das Dualsystem und das Hexadezimalsystem.
Besondere Zahlendarstellungen
Manche Zahlen können nur mit Hilfe eines Stellenwertsystems jedoch nicht dargestellt werden, insbesondere etwa die irrationalen Zahlen. Für wichtige solcher Zahlen werden dann eigene Zahlwörter oder -symbole verwendet (Beispiele dafür sind die Kreiszahl π und die eulersche Zahl e).
Verknüpfungen von Zahlen
Für Zahlen sind verschiedene mathematische Verknüpfungen definiert. Diese Verknüpfungen können z. B. Vergleiche oder Rechenoperationen.
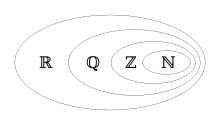
Zahlenmengen
Zahlen mit gleichen Eigenschaften fasst man zusammen, wie etwa
Zahlenmengen (bis reelle Zahlen)
- natürliche Zahlen mit der Teilmenge der Primzahlen,
- ganze Zahlen mit den Teilmengen der geraden Zahlen und der ungeraden Zahlen,
- rationale Zahlen,
- irrationale Zahlen,
- reelle Zahlen und
- komplexe Zahlen.
Siehe auch
- Arithmetik (das „Zahlenrechnen“)
- Liste besonderer Zahlen
- Zahlendarstellungen
- Zahlzeichen (oder Ziffern)
- Zahlen in unterschiedlichen Sprachen
- Bezeichnungen von Zahlen
- Numerologie
Literatur
- Heinz-Dieter Ebbinghaus et. al.: Zahlen. Springer, Berlin 1992, ISBN 3-540-55654-0.
- Georges Ifrah: Universalgeschichte der Zahlen. Parkland, Köln 1998, ISBN 3-88059-956-4.
- Wolfgang Rautenberg: Messen und Zählen, Eine einfache Konstruktion der reellen Zahlen. Heldermann Verlag, Lemgo 2007, ISBN 978-3-88538-118-1.
Weblinks
Commons: Numbers – Album mit Bildern und/oder Videos und Audiodateien
Wiktionary: Zahl – Bedeutungserklärungen, Wortherkunft, Synonyme, ÜbersetzungenKategorien:- Zahl
- Mathematischer Grundbegriff
Wikimedia Foundation.
