- Panjer Algorithmus
-
Die Panjer Rekursion (oder auch Panjer-Algorithmus) ist ein Algorithmus um die Wahrscheinlichkeitsverteilung einer speziellen zusammengesetzten Zufallsvariable
zu berechnen. Wobei sowohl
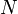 wie
wie 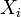 stochastisch und von einem speziellen Typ sind.
stochastisch und von einem speziellen Typ sind.Der Algorithmus wurde in einem Paper von Harry Panjer erstmals veröffentlicht [1]. Er wird im Aktuariat häufig benutzt.
Inhaltsverzeichnis
Vorbedingungen
Wir sind an der speziellen zusammengesetzten Zufallsvariablen
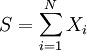 interessiert, wobei N und Xi die folgenden Vorbedingungen erfüllen müssen:
interessiert, wobei N und Xi die folgenden Vorbedingungen erfüllen müssen:Schadenanzahlverteilung
N "Schadenanzahlverteilung", d.h.
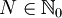 .
. 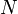 ist unabhängig von
ist unabhängig von 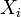 .
.Weiterhin muss N ein Element der Panjer Klasse sein. Die Panjer Klasse besteht aus allen Zähl-Zufallsvariablen, welche die folgende Relation erfüllen:
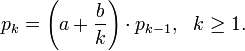 für a und b mit
für a und b mit 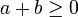 . der Wert
. der Wert 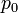 wird so bestimmt, dass
wird so bestimmt, dass 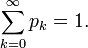
Sundt bewies im Paper [2] dass nur die Binomialverteilung, die Poissonverteilung und die Negative Binomialverteilung in der Panjer Klasse liegen. Sie haben die Parameter und Werte wie in der folgenden Tabelle beschrieben, wobei
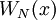 die Wahrscheinlichkeitserzeugende Funktion beschreibt.
die Wahrscheinlichkeitserzeugende Funktion beschreibt.Verteilung P[N = k] a b p0 WN(x) E[N] Var(N) Binomial 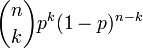
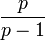
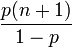
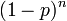
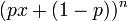
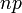
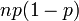
Poisson 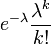
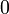
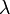
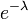

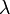
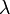
Negative Binomial 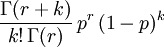
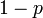
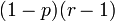
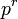
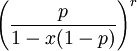
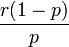
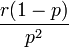
Einzelschadenverteilung
Wir nehmen an, dass
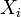 gleich verteilte unabhängige Zufallsvariablen sind welche unabhängig von
gleich verteilte unabhängige Zufallsvariablen sind welche unabhängig von 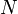 sind. Weiterhin muss
sind. Weiterhin muss 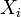 auf einem Gitter
auf einem Gitter 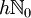 mit Gitterlänge
mit Gitterlänge 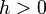 verteilt sein.
verteilt sein.Rekursion
Der Algorithmus gibt eine Rekursion um die Wahrscheinlichkeiten
![g_k =P[S = hk]\,](/pictures/dewiki/55/7e0c95c9662338046dda90176f9ad258.png) zu berechnen.
zu berechnen.Der Startwert ist:
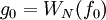
- mit den Spezialfällen
- und
die nachfolgenden Werte können folgendermaßen berechnet werden:
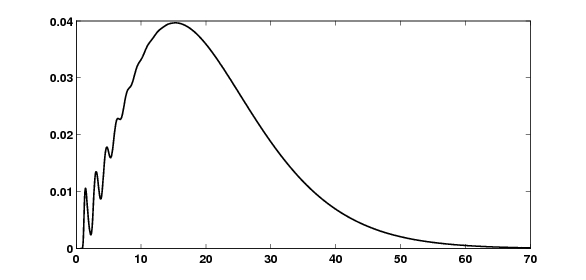
Beispiel
Das Beispiel zeigt die approximierte Dichtefunktion von
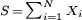 wobei
wobei 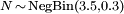 und
und 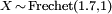 . Die Einzelschadenverteilung wurde mit einer Gitterbreite h = 0.04. diskretisiert (Siehe auch Fréchetverteilung.)
. Die Einzelschadenverteilung wurde mit einer Gitterbreite h = 0.04. diskretisiert (Siehe auch Fréchetverteilung.)Siehe auch
Referenzen
- ↑ Harry H. Panjer: Recursive evaluation of a family of compound distributions.. (PDF) In: ASTIN Bulletin. 12, Nr. 1International Actuarial Association, 1981, S. 22–26
- ↑ B. Sundt and W. S. Jewell: Further results on recursive evaluation of compound distributions. (PDF) In: ASTIN Bulletin. 12, Nr. 1International Actuarial Association, 1981, S. 27–39
Wikimedia Foundation.

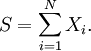
![f_k = P[X_i = hk].\,](/pictures/dewiki/48/0aec4af2d75e9eb87a5091179a297b4a.png)
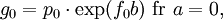
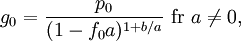
![g_k=P[S = hk] = \frac{1}{1-f_0a}\sum_{j=1}^k \left( a+\frac{b\cdot j}{k} \right) \cdot f_j \cdot g_{k-j}.](/pictures/dewiki/97/ab2afc8bc749cf54e336e66ba9d51d49.png)