Plateausches Problem

In der Mathematik besteht das Plateau-Problem darin eine Minimalfläche zu finden, die als Rand eine gegebene Kurve besitzt. Es ist benannt nach Joseph Plateau, der die Formen von Seifenhäuten in Drahtgestellen experimentell bestimmte. Erstmals mathematisch formuliert wurde das Problem 1760 durch Joseph-Louis Lagrange. Es gehört zum Gebiet der Variationsrechnung.

Lösung des Problems

Im Laufe der Zeit wurden verschiedene spezielle Formen des Problems gelöst, beispielsweise von Schwarz im Jahre 1865. 1928 löste R. Garnier das Plateau-Problem durch Lösung eines Riemann-Hilbert-Problems für polygonale Randkurven. Ein Approximationsprozess löst das Plateau-Problem dann für stetige Randkurven. Der Beweis der Existenz einer Lösung des Problems gelang jedoch erst Anfang der 1930er Jahre unabhängig voneinander Jesse Douglas und Tibor Rado mit Mitteln der direkten Methoden der Variationsrechnung (vgl. als Beispiel die Lösung des Dirichletprinzips).

Formulierung des Problems

Es sei 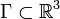$\Gamma\subset\mathbb R^3$ eine Jordankurve mit drei fest gewählten Punkten 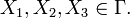$X_1,X_2,X_3\in\Gamma.$ Gesucht ist eine Abbildung 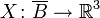$X\colon\overline B\to\mathbb R^3$ auf dem Abschluss der offenen Kreisscheibe 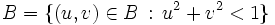$B=\{(u,v)\in B\,:\,u^2+v^2<1\}$ mit der Eigenschaft 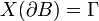$X(\partial B)=\Gamma$ mit dem Rand 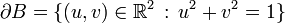$\partial B=\{(u,v)\in\mathbb R^2\,:\,u^2+v^2=1\}$ von B. Von der Abbildung X werden folgende Eigenschaften verlangt:

• Harmonizität: 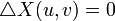$\triangle X(u,v)=0$ in B
• Konformität: | X_u(u,v) | ² = | X_v(u,v) | ² sowie 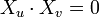$X_u\cdot X_v=0$ in B
• Topologische Randbedingung: 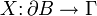$X\colon\partial B\to\Gamma$ Homöomorphismus auf Γ
• 3-Punktebedingung: X(e^{2πk / 3}) = X_k für k = 1,2,3.

Erweitertes Problem in höheren Dimensionen

Die Erweiterung des Problems auf höhere Dimensionen, also auf k-dimensionale Flächen im n-dimensionalen Raum, stellt sich dagegen als weitaus schwieriger dar. Insbesondere sind Lösungen des allgemeinen Problems nicht notwendig regulär, sondern können Singularitäten besitzen. Dies gilt stets für 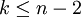$k \leq n-2$, aber auch für den Fall einer Hyperfläche, also k = n − 1, wenn $n\geq 8$.

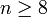Weblinks

• Douglas, Jesse (1931). "Solution of the problem of Plateau". Trans. Amer. Math. Soc. 33 (1): 263–321. doi:10.2307/1989472.
• Radó, Tibor (1930). "On Plateau's problem". Ann. of Math. (2) 31: 457–469. doi:10.2307/1968237.
• Eric Weissteins Eintrag in Mathworld
• Brian Whites Webpage
• Springer Online Reference Works