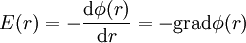Potentialfeld

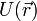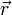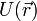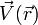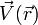Als Potentialfeld bezeichnet man ein Skalarfeld $U (\vec r)$ , das jedem Raumpunkt $\vec r$ einen Wert U zuordnet, wenn $U (\vec r)$ das Potential eines Vektorfeldes $\vec V (\vec r)$ ist. Dies ist der Fall, wenn $\vec V (\vec r) = -\operatorname{grad} ~ U (\vec r)$ gilt, d. h. wenn $\vec V (\vec r)$, der Gradient von 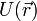$U (\vec r)$ ist. Das Vektorfeld 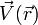$\vec V (\vec r)$ , das gelegentlich auch als "Potentialfeld" bezeichnet wird, da es ein Potential besitzt, ist rotationsfrei

$\operatorname{rot} ~ \vec V (\vec r) = \vec 0$ .

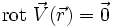Ein Umlaufintegral in einem solchen Feld ist (in einem einfach zusammenhängenden Gebiet) stets gleich Null:

$\oint \vec V (\vec r) \cdot \mathrm{d}\vec r = 0$ .

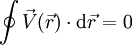Gradient eines Potentialfelds

Ein elektrisches Quellenfeld kann sowohl durch eine vektorielle Feldstärkefunktion E(r) oder E(x,y,z) als auch durch eine skalare mathematische Hilfsfunktion φ(x,y,z) die sogenannte Potentialfunktion, beschrieben werden. Beide hängen über folgende Differentialoperation miteinander zusammen:

$E(r)= -\frac{\mathrm{d}\phi(r)} {\mathrm{d}r} = -\operatorname{grad}\phi(r)$

Die Gradienten aller Raumpunkte eines elektrischen Potentialfeldes φ(r) bilden also ein Vektorfeld. Weil in den Anfängen der Elektrizitätslehre die Richtung der Feldstärke vom höheren zum niedrigeren Potential festgelegt wurde erhält der Gradient in der Elektrotechnik per definitionem ein negatives Vorzeichen. Den Differentialoperator d/dr bezeichnet man als Gradientenoperator.

Analog stellt auch ein Gravitationsfeld eine Verknüpfung von Skalar- und Vektorfeld dar: die 3 Komponenten des Feldvektors (Anziehungskraft auf die Einheitsmasse) entsprechen den partiellen Ableitungen eines Skalars, nämlich den Gradienten des Schwerepotentials.

Siehe auch

• Potentialtheorie, Gravitation, Erdschwerefeld
• Elektrodynamik, Magnetfeld, Poisson-Gleichung

Literatur und Weblinks

• Adolf J. Schwab: Begriffswelt der Feldtheorie, Springer Verlag, ISBN 3-540-42018-5
• Rudolf Sigl: Einführung in die Potentialtheorie, Wichmann-Verlag 1973.
• GSI Helmholtzzentrum für Schwerionenforschung - Vektorpotential und skalares Potential