- Potenzielle Energie
-
Die potentielle Energie (auch Höhen- oder Lageenergie) ist eine der Formen von Energie in der Physik. Es handelt sich dabei um diejenige Energie, welche ein Körper durch seine Position oder Lage in einem konservativen Kraftfeld (etwa einem Gravitationsfeld oder elektrischen Feld) enthält. Man spricht daher auch von Lageenergie. Ein bestimmter Ort in diesem Feld dient dabei als Bezugspunkt; beim Gravitationsfeld der Erde kann dies beispielsweise die Erdoberfläche sein. Die Begriffe Potential und potentielle Energie sind eng verwandt und unterscheiden sich nur um einen konstanten Faktor (in der Mechanik die Masse, in der Elektrostatik die elektrische Ladung). Als Formelzeichen für die potentielle Energie wird üblicherweise V oder Epot verwendet.
Inhaltsverzeichnis
Beispiele
Ein Turmspringer besitzt vor dem Abspringen eine potentielle Energie (im Gravitationsfeld) gegenüber der Wasseroberfläche. Das Bezugsniveau kann aber auch auf den Grund des Beckens gelegt werden, dann hat der Springer entsprechend mehr potentielle Energie. Analog muss er mehr Arbeit aufwenden, um vom Grund auf das Sprungbrett zu kommen, als wenn er lediglich die Treppe am Turm hinaufläuft. Läuft er über das Sprungbrett an, verändert sich seine potentielle Energie nicht, da er keine Arbeit gegen die senkrecht nach unten wirkende Schwerkraft verrichtet.
Die Arbeit, die der Springer aufwenden muss, und damit auch die potentielle Energie, die er auf dem Sprungturm in Bezug auf die Wasseroberfläche besitzt, berechnet sich als V = mgh wobei m die Masse des Springers, g die Erdschwerebeschleunigung und h die Höhe des Turms darstellt. Arbeit im Allgemeinen berechnet sich als das Produkt einer Kraft und des Weges, dem entlang die Kraft wirkt. In diesem Fall handelt es sich bei der Kraft um die Gravitationskraft (
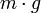 ) und bei dem Weg um die Höhe des Turms (h).
) und bei dem Weg um die Höhe des Turms (h).Auch das in einem Stausee aufgestaute Wasser, ehe es durch Fallrohre hinabstürzt, oder eine Metallkugel, welche zwischen zwei elektrisch geladenen Kondensatorplatten im Schwebezustand gehalten wird, verfügt über potentielle Energie, wenn das Bezugsniveau entsprechend darunter gewählt wird.
Formale Definition
Da ein konservatives Kraftfeld
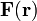 mathematisch ein Gradientenfeld ist, existiert ein skalares Feld
mathematisch ein Gradientenfeld ist, existiert ein skalares Feld 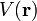 , für das die Beziehung
, für das die Beziehunggilt. Hierbei ist
 der Nabla-Operator und
der Nabla-Operator und 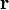 der Ortsvektor.
der Ortsvektor.Für einzelne Komponenten des Feldes bedeutet dies
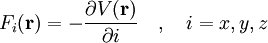 .
.
Dies kann umgeformt werden zu
Die potentielle Energie ist daher
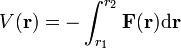 .
.
In der Elektrostatik ist das Potential des elektrischen Feldes
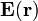
Der Zusammenhang zwischen Potential
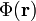 und potentieller Energie ist
und potentieller Energie ist- für eine Ladung q:
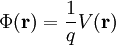
- für eine Masse m:
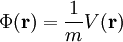
Die potentielle Energie entspricht in ihrer Größe der am Körper zu verrichtenden Arbeit, um vom Bezugsniveau die neue Lage zu erreichen. Bei reversiblen Vorgängen (keine Reibung) ist die potentielle gleich der kinetischen Energie, die der Körper gewänne, wenn er der Kraft bis auf das Bezugsniveau folgen, das heißt, sich frei bewegen könnte.
Um die potentielle Energie eines Körpers zu vergrößern, muss Arbeit gegen die Kräfte eines konservativen Kraftfeldes verrichtet werden. So besitzt jeder massebehaftete Körper in einem Gravitationsfeld potentielle Energie. Diese kann jedoch nur erhöht oder vermindert werden, wenn der Körper gegen oder in Richtung der Gravitationskraft verschoben wird.
Befindet sich der Körper auf Bezugsniveau, so ist die potentielle Energie gleich null.
Potentielle Energie und der Energieerhaltungssatz
In einem abgeschlossenen System ohne Energieaustausch mit der Umgebung und unter Vernachlässigung jedweder Reibung, gilt zu jedem Zeitpunkt der Energieerhaltungssatz der klassischen Mechanik:
- E = T + V = const.
- V - potentielle Energie
- T - kinetische Energie
- E - mechanische Energie
In Worten: Die Summe aus potentieller und kinetischer Energie, einschließlich der Rotationsenergie, ist konstant und entspricht der Gesamtenergie des mechanischen Systems.
In einer höheren Formulierung der Mechanik, dem Hamilton-Formalismus, schreibt man auch
wobei H die Hamiltonfunktion und L die Lagrangefunktion sind.
Potentielle Energie in einem Gravitationsfeld
Berechnung
Für die Funktion V(r) der potentiellen Energie eines Massepunktes m und der Masse M eines sphärischen Himmelskörpers gilt allgemein
Wobei F die von dem Himmelskörper auf den Massenpunkt ausgeübte Gravitationskraft und dr eine infinitesimale Verschiebung der Höhe des Systems bezeichnen.
Wenn der Massenpunkt von einer Höhe r1 zu einer Höhe r2 gebracht wird, so ändert sich seine potentielle Energie um
Die potentielle Energie des Massenpunktes möge auf der Planetenoberfläche Rp, also r1 = Rp, gleich null sein, womit
ist.
Damit ergibt sich für eine beliebige Höhe r mit r > Rp
Schreibt man die potentielle Energie als Funktion einer Höhe h = r − Rp über der Planetenoberfläche, so ist sie vergleichbar mit mgh.
Dann ist
Mit der Schwerebeschleunigung
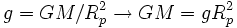 vereinfacht sich die Formel zu
vereinfacht sich die Formel zuDie potentielle Energie ist also ein mgh-faches von Rp / r. In unmittelbarer Nähe der Erdoberfläche sind Rp und r näherungsweise gleich, womit die potentielle Energie in einem solchen Fall mit mgh approximiert wird. Es ist zu beachten, dass die potentielle Energie mit steigendem r nicht unendlich anwächst, sondern vielmehr aus
ersichtlich ist, dass der zweite Term dieser Gleichung mit steigendem r gegen null strebt, weshalb sich die potentielle Energie einem maximalen Grenzwert der Größe
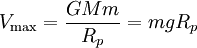 , mit
, mit 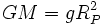
annähert, wobei g die Fallbeschleunigung auf dem Niveau von Rp ist.
Maximale potentielle Energie
Um einen Massenpunkt m um eine Strecke dr anzuheben, muss die Arbeit
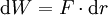 geleistet werden, wobei F der Gravitationskraft des Planeten entspricht. Um den Massenpunkt von einer Planetenoberfläche R aus dem Gravitationsfeld heraus, also in die Unendlichkeit, zu befördern, muss die maximale potentielle Energie des Gravitationsfeldes des Planeten gerade erreicht oder übertroffen werden. Für diese gilt also
geleistet werden, wobei F der Gravitationskraft des Planeten entspricht. Um den Massenpunkt von einer Planetenoberfläche R aus dem Gravitationsfeld heraus, also in die Unendlichkeit, zu befördern, muss die maximale potentielle Energie des Gravitationsfeldes des Planeten gerade erreicht oder übertroffen werden. Für diese gilt alsoIn der Kosmologie ist die sogenannte Gravitationsenergie die größte bekannte Energiequelle.
Potentielle Energie einer gespannten Feder
Aus der Federkraft
- F(x) = − kx,
ergibt sich für die potentielle Energie
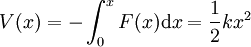 .
.
Hierbei ist k die Federkonstante und x die Auslenkung der Feder aus der Ruhelage.
Siehe auch
Wikimedia Foundation.

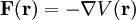
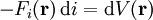
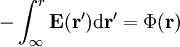
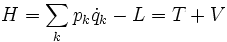
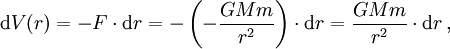
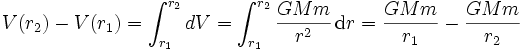
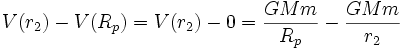
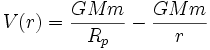
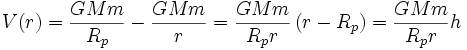
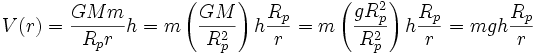
![W=V_\mathrm{max}=\int_{R}^{\infty} \mathrm{d}W=\int_{R}^{\infty} \frac{GMm}{R^2}\, \mathrm{d}R=GMm\int_{R}^{\infty} \frac{1}{R^2}\, \mathrm{d}R=GMm\left[-\frac{1}{R}\right]^\infty_R=\frac{GMm}{R}=mgR](/pictures/dewiki/52/424ab1c6212b82b70530f2570370bdec.png)