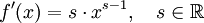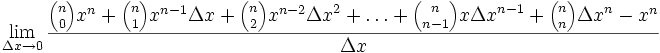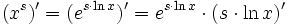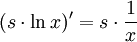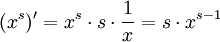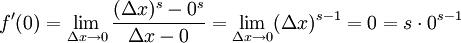- Potenzregeln
-
Die Potenzregel ist in der Mathematik eine der Grundregeln der Differentialrechnung. Sie dient der Ermittlung der Ableitung von Potenzfunktionen f(x) = xn. Sie lautet:
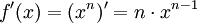 .
.
Beispielsweise ist
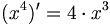 .
.Inhaltsverzeichnis
Verallgemeinerung
Die Potenzregel gilt auch für Potenzfunktionen f(x) = xs, deren Exponent (Hochzahl) s keine ganze Zahl ist:
Herleitung
1. Fall: Der Exponent ist eine natürliche Zahl
Die Ableitung einer Potenzfunktion an der Stelle x ist der Grenzwert:
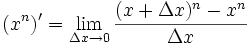 .
.
Nach dem binomischen Lehrsatz ist dies gleich
geschrieben mit so genannten Binomialkoeffizienten. Daraus folgt dann die Potenzregel:
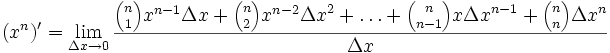
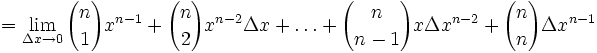
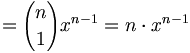 .
.
Bildlich veranschaulicht wächst ein 'n-dimensionaler Würfel' in genau n Richtungen (entlang den n Koordinatenachsen) um '(n-1)-dimensionale Würfel' an. Ein Quadrat wächst (bzw. kristallisiert) also marginal um 2 Seitenlinien, und ein Würfel wächst um 3 Quadrate.2. Fall: Beliebiger Exponent
Man benutzt die Darstellung mithilfe der Exponentialfunktion:
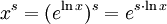 und leitet ab mithilfe der Kettenregel und der Ableitungsregel für die Exponentialfunktion:
und leitet ab mithilfe der Kettenregel und der Ableitungsregel für die Exponentialfunktion:Für die innere Ableitung benutzt man die Faktorregel und die Regel für die Ableitung der Logarithmusfunktion:
Indem man dies einsetzt und für
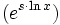 wieder xs schreibt, erhält man
wieder xs schreibt, erhält manDiese Herleitung gilt nur für
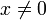 . Für s > 1 ist die Funktion f(x) = xs aber auch an der Stelle x = 0 differenzierbar und die Regel gilt auch an der Stelle x = 0. Man berechnet direkt mithilfe des Differenzenquotients:
. Für s > 1 ist die Funktion f(x) = xs aber auch an der Stelle x = 0 differenzierbar und die Regel gilt auch an der Stelle x = 0. Man berechnet direkt mithilfe des Differenzenquotients:
Wikimedia Foundation.