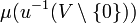Primitive Funktion

In der Mathematik, speziell in der Analysis, ist eine einfache Funktion eine Funktion, welche messbar ist und nur endlich viele Werte annimmt. Dabei ist der Wertebereich $\mathbb{R}$ oder allgemeiner ein Banach-Raum. Einfache Funktionen spielen eine zentrale Rolle in der Integrationstheorie.

Eine einfache Funktion wird auch als Elementarfunktion, fälschlicherweise auch als Treppenfunktion bezeichnet.

Definition

Sei (X,Σ) ein Messraum und V ein (reeller oder komplexer) Banach-Raum. Eine Funktion $u:X\to V$ heißt einfache Funktion, falls folgende Bedingungen erfüllt sind:

• u nimmt nur endlich viele Werte $\{v_{1},\ldots,v_{n}\}$ an
• u ist messbar, d.h u ^{− 1}(v) ist für jedes 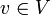$v\in V$ messbar.

Ist $u:X\to V$ sogar auf einem Maßraum (X,Σ,μ) definiert, so verlangt man manchmal noch zusätzlich, dass

• $\mu(u^{-1}(V\setminus\{0\}))$

endlich ist^[1].

Dazu äquivalent ist, dass die Funktion u eine Darstellung der Form

$u(x)=\sum^{n}_{i=1}v_i \cdot \chi_{E_i}(x)$

besitzt. Dabei ist $v_i\in V$ und $\chi_{E_i}$ bezeichnet die charakteristische Funktion der messbaren Menge $E_i \in \Sigma$. Diese Darstellung nennt man kanonisch.

Eigenschaften

Summen, Differenzen und Produkte von einfachen Funktionen sind wieder einfach, ebenso skalare Vielfache. Somit bildet der Raum der einfachen Funktionen eine kommutative Algebra über $\mathbb{R}$ bzw. $\mathbb{C}$.

Verwendung

Einfache Funktionen spielen eine zentrale Rolle bei der Definition des Lebesgue-Integrals und des Bochner-Integrals. Dabei wird das Integral zunächst für positive einfache Funktionen durch

$\int_\Omega u\,{\rm d}\mu:=\sum_{i=1}^m v_i\mu(E_i)$

definiert und dann durch Approximation auf weitere Funktionen übertragen.

Verwechslung mit Treppenfunktionen

Häufig werden einfache Funktionen mit Treppenfunktionen verwechselt. Beide Funktionen nehmen nur endlich viele Funktionswerte an. Eine Treppenfunktion besteht jedoch auch nur aus endlich vielen Intervallen, auf denen sie konstante Funktionswerte hat (Diese Funktionen werden für die Riemann-Integration verwendet). Eine einfache Funktion dagegen kann, zum Beispiel auf beliebig vielen Intervallen immer abwechselnd zwei Funktionswerte annehmen und ist damit keine Treppenfunktion mehr (insbesondere ist der Indikator der rationalen Zahlen 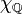$\chi_{\mathbb{Q}}$ (Dirichlet-Funktion) eine einfache Funktion - obwohl er nicht riemann-integrierbar ist).

Literatur

• R.M. Dudley: Real Analysis and Probability, Cambridge University Press, 2002, pp.114-7.
• David Meintrup, Stefan Schäffler: Stochastik : Theorie und Anwendungen, Berlin, Heidelberg, New York, Springer, 2005.

Weblinks

• Vorlesungsskript zur Analysis III, Heinrich-Heine-Universität Düsseldorf (pdf)

Einzelnachweise

1. ↑ Herbert Amann, Joachim Escher: Analysis III. 1. Auflage. Birkhäuser-Verlag, Basel/Boston/Berlin 2001, ISBN 3-7643-6613-3, Seite 65.