- Rekursive Funktion
-
Dieser Artikel erläutert die Technik der rekursiven Definition; zum Begriff rekursive Menge siehe entscheidbar. 
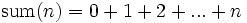
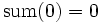
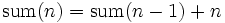
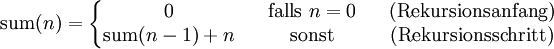
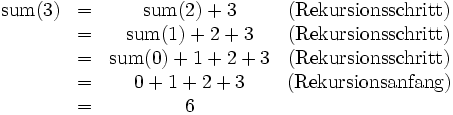
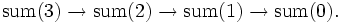
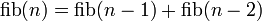für n > 1.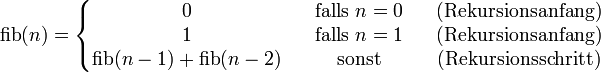
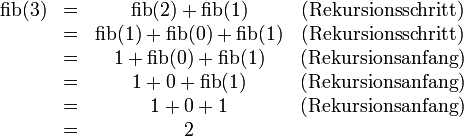
- Errichte über zwei gegebenen Punkten ein Quadrat
- Auf der Oberseite zeichne ein Dreieck mit definierten Winkeln bzw. Höhe
- Rufe diese Funktion für die beiden Schenkel dieses Dreieckes auf
- µ-Rekursion
- Rekursive Programmierung
- Euklidischer Algorithmus
- Kellerautomat
- Rekursionssatz
- Rekursives Akronym
- Türme von Hanoi – typische Anwendung von Rekursion
- Backtracking
Als Rekursion (lat. recurrere „zurücklaufen“) bezeichnet man die Technik in Mathematik, Logik und Informatik, eine Funktion durch sich selbst zu definieren (rekursive Definition). Wenn man mehrere Funktionen durch wechselseitige Verwendung voneinander definiert, spricht man von wechselseitiger Rekursion.
Nicht jede rekursive Definition ist eine Definition im eigentlichen Sinn, denn die zu definierende Funktion braucht nicht wohldefiniert zu sein. Eine hinreichende Bedingung für Wohldefiniertheit ist die Terminierung der Stützrelation. Jeder Aufruf der rekursiven Funktion muss sich durch Entfalten der rekursiven Definition in endlich vielen Schritten auflösen lassen. Umgangssprachlich sagt man, sie darf nicht in einen infiniten Regress (vulgo Endlosschleife) geraten.
Die Rekursion ist eine von mehreren möglichen Problemlösungsstrategien, sie führt oft zu eleganten Darstellungen. Auch in vielen Programmiersprachen sind rekursive Prozeduren als Sprachmittel verfügbar. Rekursion und Iteration sind im Wesentlichen gleichmächtige Sprachmittel. In ihrer Implementierung kann es Effizienzunterschiede geben.
Inhaltsverzeichnis |
Definition
(Hinweis vorab: Rekursionsverfahren und rekursive Definitionen sind nicht auf Funktionen natürlicher Zahlen beschränkt. Hier sei auf das verallgemeinerte Rekursionsschema verwiesen.)
Das Grundprinzip der rekursiven Definition einer Funktion f ist: Der Funktionswert f(n+1) einer Funktion f : N0 → N0 ergibt sich durch Verknüpfung bereits vorher berechneter Werte f(n), f(n-1), ... Falls außerdem die Funktionswerte von f für hinreichend viele Startargumente bekannt sind, kann jeder Funktionswert von f berechnet werden. Bei einer rekursiven Definition einer Funktion f ruft sich somit die Funktion so oft selbst auf, bis ein vorgegebenes Argument (meistens 0) erreicht ist.
Die Definition von rekursiv festgelegten Funktionen ist eine grundsätzliche Vorgehensweise in der funktionalen Programmierung. Ausgehend von einigen gegebenen Funktionen (wie z. B. die Summen-Funktion) werden neue Funktionen definiert. Mit diesen können weitere Funktionen definiert werden.
Ein Spezialfall der Rekursion ist die primitive Rekursion, die stets durch eine Iteration ersetzt werden kann. Bei einer solchen Rekursion enthält der Aufruf-Baum keine Verzweigungen, das heißt er ist eigentlich eine Aufruf-Kette: das ist immer dann der Fall, wenn eine rekursive Funktion sich selbst jeweils nur einmal aufruft, insbesondere am Anfang (Head Recursion, siehe Infiniter Regress) oder nur am Ende (Tail Recursion oder Endrekursion) der Funktion. Umgekehrt kann jede Iteration durch eine primitive Rekursion ersetzt werden, ohne dass sich dabei die Komplexität des Algorithmus ändert.
Formen der Rekursion
Die häufigste Rekursionsform ist die lineare Rekursion, wo in jedem Fall der rekursiven Definition höchstens ein rekursiver Aufruf vorkommen darf. Die Berechnung verläuft dann entlang einer Kette von Aufrufen.
Die primitive Rekursion ist ein Spezialfall der linearen Rekursion. Hier definiert man Funktionen auf den natürlichen Zahlen, wobei in jedem rekursiven Aufruf dessen erster Parameter um Eins abnimmt. Jede primitiv-rekursive Definition kann unter Zuhilfenahme eines Stapels durch eine For-Schleife ersetzt werden.
Die endständige oder repetitive Rekursion (Tail Recursion oder Endrekursion) bezeichnet den Spezialfall der linearen Rekursion, wo jeder rekursive Aufruf die letzte Aktion ist, das heißt, er darf keinen echten Kontext mehr haben. Endrekursionen lassen sich unmittelbar durch While-Schleifen ersetzen und umgekehrt.
Unter verschachtelter Rekursion versteht man eine Definition, wo rekursive Aufrufe in Parameterausdrücken rekursiver Aufrufe vorkommen. Diese Rekursionsform gilt als außerordentlich schwer zu durchschauen.
Kaskadenförmige Rekursion bezeichnet den Fall, wo mehrere rekursive Aufrufe nebeneinander stehen. Die rekursiven Aufrufe bilden dann einen Baum. Kaskadenförmige Rekursion gilt als elegant, kann aber ohne weitere Maßnahmen einen exponentiellen Berechnungsaufwand nach sich ziehen. Sie wird also gern als Ausgangspunkt für eine andere effizientere Formulierung gebraucht.
Die wechselseitige Rekursion bezeichnet die Definition mehrerer Funktionen durch wechselseitige Verwendung voneinander. Sie lässt sich zurückführen auf die gewöhnliche Rekursion einer tupelwertigen Funktion.
Anwendung
Im Fall von primitiv-rekursiven Funktionen steht es dem Programmierer frei, eine iterative oder eine rekursive Implementierung zu wählen. Dabei ist die rekursive Umsetzung meist eleganter, während die iterative Umsetzung effizienter ist (insbesondere weil der Stack weniger beansprucht wird und der Overhead für den wiederholten Funktionsaufruf fehlt); siehe auch das Programmierbeispiel unten.
Manche Programmiersprachen (insbesondere in der Funktionalen Programmierung) erlauben keine Iteration, sodass immer die rekursive Umsetzung gewählt werden muss. Solche Sprachen setzen häufig zur Optimierung primitive Rekursionen intern als Iterationen um (insbesondere einige Interpreter für LISP und Scheme verfahren so).
Es ist zu beachten, dass eine naive Implementierung bei manchen Funktionen (z. B. den Fibonacci-Zahlen) bedingt, dass Teillösungen mehrfach berechnet werden. Abhilfe schafft in diesem Beispiel die dynamische Programmierung, die auf der Wiederverwendung bereits berechneter Zwischenlösungen beruht. Die Rekursion ist ein wesentlicher Bestandteil einiger Entwurfsstrategien für effiziente Algorithmen, insbesondere der Teile-und-herrsche-Strategie (Divide and Conquer). Andere Ansätze (zum Beispiel sogenannte Greedy-Algorithmen) verlangen ein iteratives Vorgehen. Rekursion und primitiv-rekursive Funktionen spielen eine große Rolle in der theoretischen Informatik, insbesondere in der Komplexitätstheorie und Berechenbarkeitstheorie (siehe Lambda-Kalkül und Ackermannfunktion).
Im Compilerbau ist der rekursive Abstieg (Recursive Descent) eine Technik, bei der eine Sprache rekursiv geparst wird.
Beispiele
Die Funktion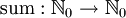 
soll zu jeder Zahl n die Summe der ersten n Zahlen berechnen. Sie ist folgendermaßen definiert:
Streng genommen ist das keine Definition, denn in einer Definition dürfen keine Auslassungszeichen vorkommen.
Um eine gleichwertige rekursive Definition der Summenfunktion zu erhalten, bestimmen wir zunächst den einfachen Fall, den Rekursionsanfang. Im Beispiel handelt es sich um den Funktionswert für 0.
Übrig bleibt der schwierige Fall, also hier der Funktionswert für n > 0. Den schwierigen Fall führen wir auf einen einfacheren Fall zurück, nämlich auf den Fall n − 1. Dieser einfachere Fall wird unser rekursiver Aufruf. Die entsprechende Vorschrift heißt Rekursionsschritt. Beispielsweise lässt sich die Summe der ersten n Zahlen berechnen, indem man die Summe der ersten n − 1 Zahlen berechnet und dazu die Zahl n addiert:
Diese beiden Gleichungen lassen sich zu einer rekursiven Definition der Summenfunktion zusammenfassen:
Wir stellen fest, dass es sich hierbei um eine lineare Rekursion handelt, denn in jedem der beiden Fälle (Rekursionsanfang und Rekursionsschritt) gibt es höchstens einen sum-Aufruf. Es ist sogar eine primitive Rekursion. Es ist aber keine Endrekursion, denn nach dem rekursiven Aufruf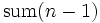 
muss noch n addiert werden.
Die Summe der Zahlen von 0 bis 3 berechnet sich dann wie folgt:
Die Aufruf-Kette dazu sieht so aus:
Es gibt auch eine Charakterisierung der Summenfunktion ohne Rekursion, denn die Gaußsche Summenformel besagt, dass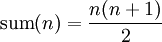 
.
Ein anderes klassisches Beispiel ist die Fibonacci-Folge
0,1,1,2,3,5,8,13,21,34,...
Die Fibonacci-Funktion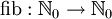 
, die jedem n die n-te Fibonacci-Zahl zuordnet, hat die einfachen Fälle 
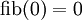und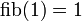 
und genügt der Rekursionsgleichung
Es ergibt sich die rekursive Definition:
Diese rekursive Definition ist kaskadenförmig. Die dritte Fibonacci-Zahl wird zum Beispiel folgendermaßen berechnet:
Die Berechnung für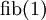 
wird hier mehrfach durchgeführt. Das deutet an, dass es Potential für Optimierungen gibt. Auch für die Fibonacci-Funktion gibt es einen gleichwertigen geschlossenen Ausdruck.
Programmierbeispiel I, Methodik rekursiver Implementation
Implementation, implementativ iterativ
Im folgenden Beispiel wird eine Zeichenkette von Offset 0 bis Offset n implementativ iterativ durchlaufen. Die Abbruchbedingung ist erfüllt, wenn der Iterator auf den Nullterminator der Zeichenkette stößt.
1 char* strKette = "foobar",
2 * pTemp = strKette;
3
4 while( *pTemp != 0x0 )
5 {
6 // z. B. Buchstabe für Buchst. ausgeben
7 ++pTemp;
8 };
Implementation, implementativ rekursiv
Jedoch lässt sich die Iteration einer Zeichenkette auch implementativ rekursiv darstellen, auch wenn die Aufgabenstellung nicht implizit rechnerisch rekursiv ist.
1 void fnTraverse( char* pString )
2 {
3 if( *pString == 0x0 )
4 return;
5 else
6 // z. B. Buchstabe für Buchst. ausgeben
7 fnTraverse( ++pString );
8 }
Programmierbeispiel II, Fakultätsberechnung
Das Beispiel zeigt eine beliebte und einfache Implementierung der Fakultätsberechnung mittels Pseudocode. Der rekursiven Variante wird hier zur Verdeutlichung eine iterative Variante gegenübergestellt. Dabei ist n die Zahl, deren Fakultät berechnet werden soll.
1 fakultät_rekursiv(n)
2 {
3 wenn n <= 1
4 dann return 1
5 sonst return ( n * fakultät_rekursiv(n-1) )
6 }
Die Rekursion kommt in Zeile 5 zum Ausdruck, wo die Funktion sich selbst mit einem um 1 verringerten Argument aufruft. Hier im nächsten Beispiel wird die Funktion nur einmal aufgerufen und arbeitet dann linear den gegebenen Algorithmus ab:
1 fakultät_iterativ(n)
2 {
3 fakultät = 1
4 faktor = 2
5 solange faktor <= n
6 {
7 fakultät = fakultät * faktor
8 faktor = faktor + 1
9 }
10 return fakultät
11 }
Rekursive Grafiken
Nicht nur Funktionen, sondern auch Punktmengen können rekursiv definiert werden (Fraktale). Deren graphische Darstellung liefert ästhetisch ansprechende, natürlich aussehende Gebilde. Ein Beispiel ist der rekursive Pythagoras-Baum. Der rekursive Algorithmus sieht folgendermaßen aus:
Der Algorithmus wird dann bis zu einer vorgegebenen Rekursionstiefe entfaltet. Bei Rekursionstiefe eins entsteht ein Dreieck mit je einem Quadrat über den drei Seiten. Das sieht wie die Illustration zum Satz des Pythagoras aus --- daher der Name. Je höher die Rekursiontiefe, desto mehr ähnelt das Gebilde einem Baum.
Lösen von Rekursionen
Beim Lösen einer Rekursion sucht man zum einen den Laufzeitaufwand, zum anderen die explizite Form der Rekursion.
Der Aufwand kann als asymptotische Θ- bzw. Ο-Schranke mittels Mastertheorem bzw. Substitutionsmethode bestimmt werden. Auch das geschickte Raten mit anschließender Induktion bietet eine Möglichkeit, eine Oberschranke der Laufzeit zu ermitteln.
Die explizite Form (oder auch geschlossene Form genannt) der Rekursionsgleichung lässt sich beispielsweise durch die Erzeugende-Funktion finden. Eine zweite Möglichkeit bietet das Ableiten durch Differenzenbildung aufeinanderfolgender Funktionswerte der Rekurrenz.
Probleme mit Rekursionen
Wird eine Rekursion zu häufig durchgeführt, so kann das Computerprogramm abstürzen, weil der Speicher irgendwann nicht mehr ausreicht. Bei jedem Aufruf wird der Stack neu beschrieben, allerdings werden die alten Variablen und Adressen manchmal dabei nicht zerstört. Es empfiehlt sich daher den Speicher per Hand freizugeben (falls dies möglich ist) oder auf Rekursive Programmierung zu verzichten, da sich viele Probleme auch mit Schleifen lösen lassen.
Siehe auch
Wikimedia Foundation.
