Primitive Elementarzelle

Die Bestandteile der Kristallstruktur

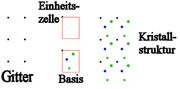
Eine Elementarzelle (manchmal auch Einheitszelle genannt) ist eine Einheit, aus der durch wiederholte Translation in drei Richtungen ein Kristallgitter aufgebaut werden kann. Sie wird durch sechs Gitterparameter definiert und enthält alle vorhandenen Symmetrieelemente. Für ein gegebenes Kristallgitter gibt es jedoch nicht nur eine, sondern unendlich viele Möglichkeiten, eine, unter Umständen sogar sehr große, Elementarzelle zu definieren.

Im Gegensatz zur Basis einer Kristallstruktur wird die Elementarzelle nicht über die darin angeordneten Atome, Ionen oder Moleküle definiert. Sie stellt das Parallelepiped dar, das durch die Grundvektoren, die zwischen den beliebig in der Basis definierten Bezugspunkten (bilden das spätere Gitter), gezogen werden, aufgespannt wird. Die Elementarzelle hat je einen Gitterpunkt an ihren Ecken (siehe Illustration; dort ist der Bezugspunkt die linke obere Ecke). Wie erwähnt, muss sie aber nicht zwischen direkt benachbarten Punkten gezogen werden, sondern kann beliebig groß gewählt werden.

Eine primitive Elementarzelle ist eine Elementarzelle kleinstmöglichen Volumens, also mit so wenigen Atomen wie möglich. Eine Möglichkeit, für jedes Kristallgitter eine primitive Elementarzelle zu finden, ist die Wigner-Seitz-Zelle, es können aber auch andere primitive Zellen konstruiert werden.

Allerdings gibt es viele Kristallgitter, bei denen die Symmetrie deutlicher erkennbar wird, wenn man keine primitive Elementarzelle sondern eine größere Zelle für die Darstellung wählt. Es wird daher oft als Elementarzelle die kleinste Zelle verwendet, die folgende zusätzliche Anforderungen erfüllt:

• Gegenüberliegende Flächen sind parallel, und die Elementarzelle ist ein Parallelepiped.
• Die Elementarzelle sollte möglichst klein sein, aber die volle Symmetrie des Gitters darstellen. Ihre Koordinatenachsen sollten sich nach Möglichkeit unter einem Winkel von 90° oder 120° schneiden.
• Das Koordinatensystem ist ein Rechtssystem. Die Kantenlängen werden mit a, b und c, die einschließenden Winkel mit α, β und γ bezeichnet.

Es zeigt sich, dass es dafür sieben verschiedene Achsensysteme, die sog. Kristallsysteme gibt. Eines davon ist das kubische System, in dem eine würfelförmige Elementarzelle gewählt werden kann (gleiche Kantenlängen, alle Winkel gleich 90°).

Im Gegensatz zu diesen nach größtmöglicher Symmetrie ausgewählten Achsensystemen erhält man für die Anordnung der primitiven Elementarzellen insgesamt 14 Möglichkeiten, Gitter verschiedener Symmetrie aufzubauen. Diese sind als die 14 Bravais-Gitter bekannt.

Kubisch raumzentrierte Elementarzelle eines Eisenkristalls

Viele aus nur einem Element bestehenden Kristallstrukturen lassen sich direkt einem der 14 Bravais-Gitter zuordnen. In diesen Kristallstrukturen gibt es also primitive Elementarzellen, die nur ein Atom enthalten; es gibt aber oft eine andere, symmetrische Elementarzelle, die gerne zur Darstellung gewählt wird. Ein Beispiel ist das kubisch raumzentrierte Gitter (siehe Bild), bei dem die kubische Elementarzelle zwei Atome enthält, eines in der Mitte, und ein Eckatom (beim Abzählen der Atome ist zu berücksichtigen, dass die 8 Eckatome zu jeweils 8 angrenzenden Zellen gehören, daher nur zu 1/8 gezählt werden dürfen). Es lässt sich hingegen keine würfelförmige primitive Elementarzelle (Elementarzelle mit nur einem Atom) finden.

Auch bei komplizierteren Substanzen wird gerne eine symmetrische Elementarzelle für die Darstellung herangezogen. Beispielsweise hat Natriumchlorid (Kochsalz) in der würfelförmigen Elementarzelle insgesamt vier Chlorid- und vier Natriumionen; hingegen nur je ein Na- und ein Cl-Atom in einer primitiven Elementarzelle.

Siehe auch: Packungsdichte, Koordinationszahl