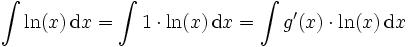- Produktintegration
-
Die partielle Integration, auch Produktintegration genannt, ist in der Integralrechnung eine Möglichkeit zur Bestimmung von Stammfunktionen. Sie kann als die Umkehrung der Produktregel der Differentialrechnung aufgefasst werden.
Für die partielle Integration verwendet man die folgende Regel, die für stetig differenzierbare Funktionen f und g gilt:
Diese Regel ist insbesondere dann von Vorteil, wenn durch Ableiten von f eine einfachere Funktion entsteht.
Inhaltsverzeichnis
Herleitung
Die Produktregel (Ableitung von Produkten) besagt:
Daraus folgt für die partielle Integration:
Folglich gilt für bestimmte Integrale:
oder dasselbe, wie man es in vielen Mathematikbüchern finden kann:
Für die konkrete Ausführung ist es oft übersichtlicher sich zunächst auf das unbestimmte Integral zu beschränken, da die unnötigen Grenzen die Sicht auf das Wesentliche versperren.
Beispiel
Als Beispiel wird das Integral
berechnet. Man sucht sich nun ein möglichst leicht zu integrierendes g'(x) und ein ebenfalls leicht ableitbares f(x). Nehmen wir nun als
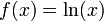 und als
und als 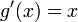 , da die Integration von
, da die Integration von 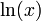 erneut den Anteil
erneut den Anteil 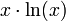 ergibt. Nun leiten wir
ergibt. Nun leiten wir 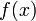 ab und integrieren
ab und integrieren 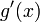 :
: 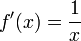 und
und 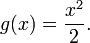
Dies ergibt dann folgende Formel:
Alternative Schreibweise
Es seien
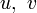 beliebige Funktionen,
beliebige Funktionen, 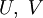 Stammfunktionen von u und v, sowie
Stammfunktionen von u und v, sowie 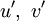 die Ableitungen von u und v.
die Ableitungen von u und v.u ist die Funktion, die man bevorzugt ableiten möchte, v ist die Funktion, die man bevorzugt integrieren möchte. Dann gilt:
Mehrdimensionale partielle Integration
Die partielle Integration in mehreren Dimensionen ist ein Sonderfall des Gaußschen Integralsatzes: Sei
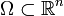 kompakt mit abschnittsweise glattem Rand
kompakt mit abschnittsweise glattem Rand 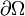 . Der Rand sei orientiert durch ein äußeres Normalen-Einheitsfeld
. Der Rand sei orientiert durch ein äußeres Normalen-Einheitsfeld  . Sei ferner
. Sei ferner  ein stetig differenzierbares Vektorfeld auf einer offenen Umgebung von Ω und
ein stetig differenzierbares Vektorfeld auf einer offenen Umgebung von Ω und  ein stetig differenzierbares Skalarfeld auf Ω. Dann gilt
ein stetig differenzierbares Skalarfeld auf Ω. Dann giltmit der Abkürzung
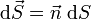 . Dann folgt die Verallgemeinerung der partiellen Integration in mehreren Dimensionen
. Dann folgt die Verallgemeinerung der partiellen Integration in mehreren Dimensionen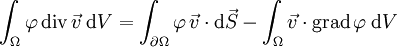 .
.
Methoden der partiellen Integration
Zur effektiven Nutzung der partiellen Integration gibt es verschiedene Standardtricks.
Beispiel 1
Manchmal kann man es sich zunutze machen, dass nach mehreren Schritten der partiellen Integration das ursprüngliche Integral auf der rechten Seite des Gleichheitszeichens wiederkehrt, welches man dann durch Äquivalenzumformung mit dem ursprünglichen Integral auf der linken Seite zusammenfassen kann.
Setzt man f(x) = cos(x) und g'(x) = sin(x), so ergibt sich
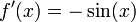 und
und 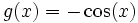
und man erhält
Addiert man auf beiden Seiten der Gleichung das Ausgangsintegral, ergibt sich:
Dividiert man beide Seiten durch 2, so erhält man schließlich:
Beispiel 2
Bei manchen Integralen bietet es sich an, für g'(x) einen Term zu wählen, der sich bei der Integration nicht oder nur unwesentlich verändert, beispielsweise die Exponentialfunktion oder die trigonometrischen Funktionen. Dann kann der andere Term "abgeräumt" werden.
Setzt man jedes Mal g'(x) = ex und für f(x) den übrigen Term unter dem Integral, so ergibt sich
Beispiel 3
Steht nur ein Term unter dem Integral, auf dessen Stammfunktion ohne Tabellenwert nicht ohne weiteres zu schließen ist, kann man gelegentlich durch Einfügen des (unsichtbar vorhandenen) Faktors "1" partiell integrieren.
Setzt man
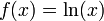 und
und 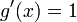 , so erhält man
, so erhält man .
.
Literatur
- Otto Forster: Analysis 1. Differential- und Integralrechnung einer Veränderlichen. Vieweg, Braunschweig 72004. ISBN 3-528-67224-2
- Konrad Königsberger: Analysis 1 Springer, Berlin 2004, ISBN 3-540-41282-4
Wikimedia Foundation.

![\int_a^b f(x)\cdot g'(x)\,\mathrm{d}x
= [f(x)\cdot g(x)]_{a}^{b} - \int_a^b f'(x)\cdot g(x)\,\mathrm{d}x.](/pictures/dewiki/49/11e7c88703f100ef6b6c1417e08344b0.png)
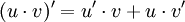
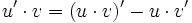
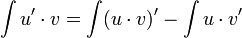
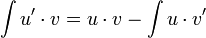
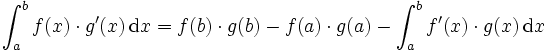
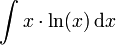
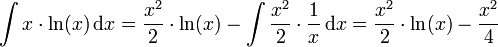
![\begin{align}
\int_a^b u(x)\cdot v(x)\,\mathrm{d}x
&= u(b)\cdot V(b) - u(a)\cdot V(a) - \int_a^b u'(x)\cdot V(x)\,\mathrm{d}x \\
&= [u(x)\cdot V(x)]_{a}^{b} - \int_a^b u'(x)\cdot V(x)\,\mathrm{d}x
\end{align}](/pictures/dewiki/98/be89652649d9b839a41c90a159e62eac.png)
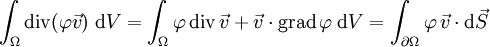
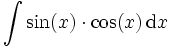
![\int \sin(x) \cdot \cos(x) \,\mathrm{d}x = [- \cos^2(x)] - \int \sin(x) \cdot \cos(x) \,\mathrm{d}x.](/pictures/dewiki/97/a9eec14213bc43eff365af8b8750db30.png)
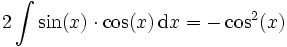


![\begin{align}
\int e^x \cdot (2-x^2) \,\mathrm{d}x & = [e^x \cdot (2-x^2)] - \int e^x \cdot (-2x) \,\mathrm{d}x \\
& = [e^x \cdot (2-x^2)] + [e^x \cdot 2x] - \int 2 \cdot e^x \,\mathrm{d}x \\
& = [e^x \cdot (2-x^2)] + [e^x \cdot 2x] - [2 \cdot e^x] \\
& = [e^x \cdot (2-x^2 +2x -2)] \\
& = [e^x \cdot (2x-x^2)] + C
\end{align}](/pictures/dewiki/50/248619a7cfbcd4a9308c81546ddb21d7.png)