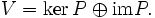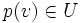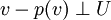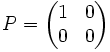Projektionsabbildung

In der Mathematik ist eine Projektion oder ein Projektor eine idempotente lineare Abbildung eines Vektorraumes V in sich selbst. Das Bild einer Projektion ist entweder ein niedrigerdimensionaler Teilraum von V oder V selbst. Bei geeigneter Wahl einer Basis von V setzt die Projektion einige Komponenten eines Vektors auf Null und behält die Übrigen bei. Damit ist auch anschaulich die Bezeichnung Projektion gerechtfertigt, wie etwa bei der Abbildung eines Hauses in einem zweidimensionalen Grundriss.

Eigenschaften

Für jede Projektion P gilt per definitionem P² = P. Eine Projektion kann nur die Eigenwerte 0 und 1 haben. Die Eigenräume sind

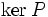• $\ker P$ zum Eigenwert 0
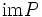• $\operatorname{im}P$ zum Eigenwert 1.

Der gesamte Raum ist die direkte Summe dieser beiden Unterräume:

$V=\ker P\oplus\operatorname{im}P.$

Die Abbildung P ist anschaulich gesprochen eine Parallelprojektion auf 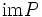$\operatorname{im}P$ entlang $\ker P$.

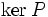Ist P eine Projektion, so ist auch 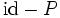$\operatorname{id}-P$ eine Projektion, und es gilt

$\ker P = \operatorname{im}(\operatorname{id}-P),\quad\operatorname{im}P=\ker(\operatorname{id}-P).$

Projektionen und Komplemente

Ist V ein Vektorraum und U ein Unterraum, so gibt es im Allgemeinen viele Projektionen auf U, d.h. Projektionen, deren Bild U ist. Ist P eine Projektion mit Bild U, so ist 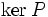$\ker P$ ein Komplement zu U in V. Ist umgekehrt W ein Komplement von U in V, so ist die kanonische Abbildung

$V=U\oplus W\to U\to V$

eine Projektion mit Bild U. Projektionen mit vorgegebenem Bild und Komplemente entsprechen einander also.

Orthogonale Projektion

Ist insbesondere V ein endlichdimensionaler reeller oder komplexer Vektorraum mit einem positiv definiten Skalarprodukt, so gibt es zu jedem Unterraum U die Projektion entlang des orthogonalen Komplementes von U, welche orthogonale Projektion auf U genannt wird. Sie ist die eindeutig bestimmte Abbildung 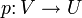$p\colon V\to U$, für die

• $p(v)\in U$

und

• $v-p(v)\perp U$

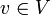für alle $v\in V$ gilt.

Ist V ein unendlichdimensionaler Hilbertraum, so gelten diese Aussagen entsprechend für abgeschlossene Unterräume U. Diese Aussage wird häufig auch als Projektionssatz bezeichnet. Ist I eine höchstens abzählbare Indexmenge und 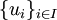$\{u_i\}_{i\in I}$ eine Orthonormalbasis von U, so ist die Orthogonalprojektion auf U gegeben durch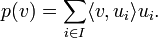

$p(v) = \sum_{i\in I} \langle v,u_i\rangle u_i.$

Diese Reihe konvergiert absolut (in V) nach der Besselschen Ungleichung (bzw. der Parsevalschen Gleichung).

Beispiel

P sei die Abbildung der Ebene 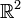$\mathbb{R}^2$ in sich, die durch die Matrix

$P=\begin{pmatrix}1&0\\0&0\end{pmatrix}$

beschrieben ist. Sie projiziert einen Vektor $\begin{pmatrix}x\\y\end{pmatrix}$ orthogonal auf die x-Achse.

Der Eigenraum zum Eigenwert 0 wird von 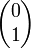$\begin{pmatrix}0\\1\end{pmatrix}$, der Eigenraum zum Eigenwert 1 von 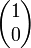$\begin{pmatrix}1\\0\end{pmatrix}$ aufgespannt.

Der Projektor 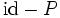$\operatorname{id}-P$ ist die Projektion auf die y-Achse.