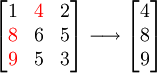Maximal-Intensitäts-Projektion

Animierte MIP-Darstellung der 3D-MRT-Aufnahme einer Kiwi (in Falschfarben eingefärbt).

Animierte MIP-Darstellung einer ¹⁸F-FDG-PET-Ganzkörper-Aufnahme.

Die Maximumintensitätsprojektion (MIP, engl. maximum intensity projection) ist ein Verfahren aus der Bildverarbeitung, das vor allem in der medizinischen Diagnostik angewendet wird. Die Maximumintensitätsprojektion rechnet dreidimensionale Bilddatensätze in zweidimensionale Projektionsbilder um, indem entlang der Blickrichtung (Projektionsrichtung) jeweils der Datenpunkt mit der maximalen Intensität ausgewählt wird. Ein wichtiger Anwendungsbereich von Maximumintensitätsprojektionen ist die Darstellung von CT-Angiographie- und Magnetresonanzangiographie-Daten; in diesen Daten haben die Blutgefäße im allgemeinen hohe Signalintensitäten und werden daher durch die Maximumintensitätsprojektion gut sichtbar abgebildet.^[1] Weitere Anwendungen sind die Darstellung von nuklearmedizinischen PET- oder SPECT-Daten.

Maximumintensitätsprojektionen werden oft genutzt, um dreidimensionale Datensätze wie in den nebenstehenden Bildbeispielen als rotierende Animation darzustellen. Hierfür werden die MIPs aus vielen unterschiedlichen Blickwinkeln berechnet und nacheinander angezeigt.

Häufig ergibt sich durch die Maximumintensitätsprojektion ein halbtransparenter Bildeindruck wie in den nebenstehenden Bildbeispielen. Durch die fehlende Perspektive ist nicht zu unterscheiden, ob Strukturen vorne (nahe am Betrachter) oder hinten im Objekt liegen. Als Folge kann beim Betrachten von animierten MIPs der Eindruck entstehen, dass sich die Drehrichtung ändert.

Funktionsprinzip

Das Prinzip der Maximumintensitätsprojektion lässt sich am einfachsten in einem zweidimensionalen Beispiel verdeutlichen, von dem eindimensionale Projektionen berechnet werden sollen. Als Beispieldatensatz dient hier eine 3×3-Matrix; zunächst wird die Maximumintensitätsprojektion in horizontaler Projektionsrichtung berechnet:

$\begin{bmatrix} 1&{\color{Red}4}&2\\{\color{Red}8}&6&5\\{\color{Red}9}&5&3 \end{bmatrix} \longrightarrow \begin{bmatrix} 4\\8\\9 \end{bmatrix}$

Aus jeder Zeile der Matrix wird jeweils der maximale Wert (rot markiert) genommen. Die Maximumintensitätsprojektion unterscheidet sich somit von einer gewöhnlichen Projektionsabbildung, wie sie beispielsweise beim konventionellen Röntgen auftritt, darin, dass das Maximum anstelle des Mittelwerts über alle Werte in Projektionsrichtung gebildet wird.

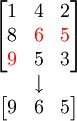
Analog erfolgt die Berechnung der Maximumintensitätsprojektion in vertikaler Richtung:

$\begin{array}{c}\begin{bmatrix} 1&4&2\\8&{\color{Red}6}&{\color{Red}5}\\{\color{Red}9}&5&3 \end{bmatrix} \\ \downarrow \\ \begin{bmatrix} 9&6&5\end{bmatrix}\end{array}$

Durch Interpolation der Daten ist auch die Berechnung in beliebige andere Projektionsrichtungen möglich.

Bezeichnung

Statt der Bezeichnung Maximumintensitätsprojektion wird in deutschsprachigen Texten häufig der englische Begriff maximum intensity projection unübersetzt verwendet. Gelegentlich findet man auch die Bezeichnung Maximalintensitätsprojektion.

Varianten

Häufig wird nicht die Projektion durch den gesamten 3D-Datensatz berechnet, sondern nur durch ein scheibenförmiges Teilvolumen (Subvolumen), das zum Beispiel aus einer gewissen Zahl aufeinanderfolgender Schichten bestehen kann. Diese Subvolumen-Maximumintensitätsprojektion wird auch als Thin-slab MIP oder kürzer als ThinMIP bezeichnet, da sie aus einer dünnen Scheibe (engl. thin slab) und nicht aus dem (dickeren) Gesamtdatensatz berechnet wird. Um den gesamten Datensatz auf diese Weise abzubilden, kann das Gesamtvolumen in zahlreiche (parallele) Teilvolumina unterteilt werden, aus denen jeweils eine Subvolumen-MIP berechnet wird; diese Technik wird als gleitende Subvolumen-MIP (engl. sliding thin-slab MIP) bezeichnet.^[2]

Bei der Minimumintensitätsprojektion (MinIP, engl. minimum intensity projection) werden anstelle der maximalen Intensitäten die jeweils minimalen Intensitäten in Blickrichtung ausgewählt. Dieses Verfahren wird beispielsweise für die Darstellung von solchen MR-Angiographie-Daten eingesetzt, bei denen die Gefäße aufgrund der verwendeten Technik dunkel statt hell erscheinen wie etwa in suszeptibilitätsgewichteten Aufnahmen der Hirnvenen (MR-Phlebographie).^[3] Die Minimumintensitätsprojektion wird beinahe immer als Subvolumen-MinIP berechnet.

In der Computertomographie wird die Minimumintensitätsprojektion für die Darstellung der Lunge und speziell der signalarmen Bronchien benutzt.^[4]

Literatur

• Mathias Goyen (Hrsg.): MR-Angiographie mit Vasovist. ABW Wissenschaftsverlag, Berlin 2007, ISBN 3-936072-52-3 (google books)

Einzelnachweise

1. ↑ Edelman RR, Wentz KU, Mattle H, Zhao B, Liu C, Kim D, Laub G: Projection arteriography and venography: initial clinical results with MR. In: Radiology 172, Nr. 2, 1989, S. 351-357 (PMID 2748814; PDF; 1,75 MiByte).
2. ↑ Napel S, Rubin GD, Jeffrey RB Jr.: STS-MIP: a new reconstruction technique for CT of the chest. In: J. Comput. Assist. Tomogr. 17, Nr. 5, 1993, S. 832-838 (PMID 8370848).
3. ↑ Reichenbach JR, Essig M, Haacke EM, Lee BC, Przetak C, Kaiser WA, Schad LR: High-resolution venography of the brain using magnetic resonance imaging. In: MAGMA Magn. Reson. Mater. Phy. 6, Nr. 1, 1998, S. 62-69 (PMID 9794291; doi:10.1016/S1352-8661(98)00011-8).
4. ↑ Bhalla M, Naidich DP, McGuinness G, Gruden JF, Leitman BS, McCauley DI: Diffuse lung disease: assessment with helical CT - preliminary observations of the role of maximum and minimum intensity projection images. In: Radiology 200, Nr. 2, 1996, S. 341-347 (PMID 8685323; PDF; 1,65 MiByte).