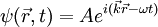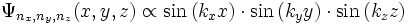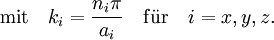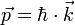- Ausbreitungsrichtung
-
Der Wellenvektor ist ein Begriff aus der Physik und gibt die Ausbreitungsrichtung einer Welle an. Er wird meistens mit
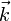 bezeichnet.
bezeichnet.Inhaltsverzeichnis
Beschreibung
Eine ebene Welle, die sich in
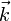 -Richtung ausbreitet, lässt sich beispielsweise in der Form
-Richtung ausbreitet, lässt sich beispielsweise in der Formschreiben.
Mit den Komponenten in x-, y- und z-Richtung
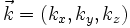
zeigt der Wellenvektor im 3-dimensionalen k-Raum, auch reziproker Raum genannt, in eine bestimmte Richtung.
Der Betrag des Wellenvektors ist die Kreis-Wellenzahl k, daher auch die Bezeichnung Wellenzahlvektor:
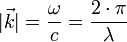
wobei λ die Wellenlänge ist.
Wellenvektor und Quantenzahlen
Der Wellenvektor ist nicht immer quantisiert. So kann die Wellenlänge eines Photons im Vakuum jeden positiven Wert annehmen (dagegen kann seine Energie nur
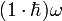 annehmen).
annehmen).Anders verhält es sich mit Teilchen in einem endlichen Raum, beispielsweise in einem Potentialtopf oder einem Elektron in einem endlich ausgedehnten Festkörper. Hier sind die erlaubten Wellenvektoren quantisiert, wenngleich sie selbst keine Quantenzahlen darstellen. Der Wellenvektor ist vielmehr eine Funktion von Quantenzahlen, bzw. können seine möglichen Werte durch Quantenzahlen abgezählt werden. Dies ist in Analogie zu den Eigenenergien eines quantenmechanischen Problems mit einem diskreten Spektrum En zu sehen: Der Index n der diskreten Energie ist die Quantenzahl, nicht jedoch die Energie selbst.
Veranschaulichung: Die Lösungen der Schrödingergleichung eines dreidimensionalen, unendlich hohen Potentialtopfs lauten
Die Zustände des Teilchens, das als Welle beschrieben wird, sind also durch die Quantenzahlen nx, ny und nz charakterisiert. Anstatt einen Zustand durch dieses Zahlentripel zu benennen, kann auch der Wellenvektor
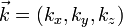 verwendet werden. Jedoch darf dieser oder einer seiner Komponenten nicht als Quantenzahl bezeichnet werden, weil der Wellenvektor zum einen dimensionsbehaftet ist und zum anderen durch reelle Zahlen dargestellt ist.
verwendet werden. Jedoch darf dieser oder einer seiner Komponenten nicht als Quantenzahl bezeichnet werden, weil der Wellenvektor zum einen dimensionsbehaftet ist und zum anderen durch reelle Zahlen dargestellt ist.Bei einem Potentialtopf mit n Teilchen ergeben sich n Vektoren im k-Raum. Wenn es sich um Elektronen, also Fermionen handelt, gibt es pro Wellenvektor zwei Zustände, die sich im Spin unterscheiden.
Wellenvektor und Impuls
Bei Photonen (Einstein-Gleichungen) sowie bei Materiewellen (de-Broglie-Relation) gibt der Wellenvektor über einen einfachen, proportionalen Zusammenhang deren vektoriellen Impuls an:
Siehe auch
Wikimedia Foundation.