Reduktion (Formale Sprachen)

Eine Ableitung ist in der Theoretischen Informatik eine Folge von Ableitungsschritten, die anhand einer formalen Grammatik ein Wort einer formalen Sprache erzeugt. Zur übersichtlichen Darstellung dieser Schritte verwendet man häufig Syntaxbäume.

Umgekehrt kann ein Wort (der Eingabetext) auch anhand der Grammatik zerlegt werden, um diejenige Ableitung zu erhalten, die dieses Wort produziert. Diesen Vorgang nennt man auch parsen. Die umgekehrt durchlaufene Folge der Ableitungsschritte nennt man auch die Reduktion des Wortes.

Ableitungssysteme werden häufig als Semi-Thue-System angegeben.

Formale Definition

Für eine formale Grammatik 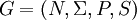$G = \left(N, \Sigma, P, S \right)$ bezeichnet eine Ableitung von w_n eine Folge von Worten 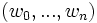$\left(w_0 , ..., w_n \right)$ mit w₀ = S, 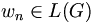$w_n \in L(G)$ und $w_0 \Rightarrow_G w_1 \Rightarrow_G \cdots \Rightarrow_G w_n$.

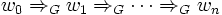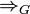$\Rightarrow_G$ symbolisiert hierbei die so genannte Transitionsrelation, also einen Ableitungsschritt. Jeder Schritt verwendet genau eine Produktion der Grammatik.

Beispiel

Die Syntax einer Programmiersprache wird im allgemeinen über eine formale Grammatik definiert. In diesem Beispiel wird nun der Aufruf von Unterprogrammen mit Parametern betrachtet.

In der Sprache Pascal kann beispielsweise ein Unterprogramm mit

PROCEDURE example(A, B: integer; VAR C: result); BEGIN ... END;

definiert und später dann über

example(2*X,Y,W);

aufgerufen werden.

Ein möglicher Ausschnitt der formalen Grammatik zur Syntaxdefinition in erweiterter Backus-Naur-Notation könnte dann sein:

procedure_declaration = PROCEDURE name
                          '(' formal_parameter_list ')' block ';' .
block = BEGIN ... END .
formal_parameter_list = parameter { ';' parameter } .
parameter = [ VAR ] name ':' name .
...
procedure_call = identifier '(' actual_parameter_list ')' ';' .
actual_parameter_list = expression { ',' expression } .

Symbole sind hier die Nichtterminale procedure_declaration, identifier, formal_parameter_list und die Terminalsymbole '(', ':', VAR usw. Eine Symbolkette auf der rechten Seite des Gleichheitszeichens wird, falls sie auftritt, durch das Symbol auf der linken Seite ersetzt. Die Symbolkette und damit das ersetzte Symbol kann wiederum Teil einer Symbolkette sein.

Ein gegebener Programmtext ist syntaktisch korrekt, wenn er durch die Umwandlungsregeln (Produktionen) der formalen Grammatik auf das Startsymbol, in diesem Beispiel program, reduziert werden kann.

Hätte man eine Sprache, die definiert wird durch

program = PROGRAM declarations program_block .
declarations = { procedure_declaration } .
program_block = BEGIN { procedure_call } END '.' .

so bestünde ein konkretes Programm nur aus Unterprogramm-Deklarationen und Aufrufen: Das reale Programm

PROGRAM
   PROCEDURE p1(a: integer; b: integer)
     BEGIN ... END;
   PROCDURE p2(VAR x: integer)
     BEGIN ... END;
BEGIN
    p1(0,1);
    p2(y);
END.

könnte man mit obenstehendem (unvollständigen) Grammatikausschnitt reduzieren, d.h. eine Ableitung erzeugen:

Schritt 1:

PROGRAM
   PROCEDURE name(name: name; name: name)
     block;
   PROCEDURE name(VAR name: name)
     block;
BEGIN
    name(expression,expression);
    name(expression);
END.

Schritt 2:

PROGRAM
   PROCEDURE name(formal_parameter_list)
     block;
   PROCEDURE name(formal_parameter_list)
     block;
BEGIN
    name(actual_parameter_list);
    name(actual_parameter_list);
END.

Schritt 3:

PROGRAM
   procedure_declaration
   procedure_declaration
BEGIN
    procedure_call
    procedure_call
END.

Schritt 4:

PROGRAM
  declarations
  program_block

Schritt 5:

program

Das Programm ist damit syntaktisch korrekt. In einem realen Parser für die Sprache Pascal würden nun aber zusätzlich so genannte semantische Prüfungen durchgeführt, insbesondere die Typprüfung - solche Prüfungen lassen sich meist auch syntaktisch überprüfen, das wäre aber sehr aufwändig. Deshalb werden hier andere Mittel verwendet. Zudem bleiben die semantischen Aspekte der Programmiersprache in diesem Zusammenhang undefiniert, sie zu betrachten ist Aufgabe der formalen Semantik.

Siehe auch

• Rechtsableitung
• Mehrdeutige Grammatik