- Reduktionsverfahren
-
Das Reduktionsverfahren von d’Alembert ist ein Verfahren aus der Theorie gewöhnlicher Differentialgleichungen. Es wird verwendet, um eine lineare Differentialgleichung n-ter Ordnung mit nicht-konstanten Koeffizienten unter Kenntnis einer (ggf. geratenen) Lösung des homogenen Problems auf eine lineare Differentialgleichung (n − 1)-ter Ordnung zurückzuführen.
Grob gesagt, gilt Folgendes: Um eine (inhomogene) lineare Differentialgleichung n-ter Ordnung
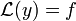 zu lösen, beschaffe man sich (auf irgendeine Weise, beispielsweise durch Raten) eine nichttriviale Lösung der zugehörigen homogenen linearen Differentialgleichung
zu lösen, beschaffe man sich (auf irgendeine Weise, beispielsweise durch Raten) eine nichttriviale Lösung der zugehörigen homogenen linearen Differentialgleichung 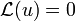 . Dann führt der Ansatz
. Dann führt der Ansatz 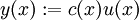 für die ursprüngliche Gleichung
für die ursprüngliche Gleichung 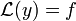 auf eine (inhomogene) lineare Differentialgleichung
auf eine (inhomogene) lineare Differentialgleichung 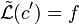 der niedrigeren Ordnung n − 1 für
der niedrigeren Ordnung n − 1 für 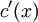 .
.Formulierung des Satzes
Man betrachte den Differentialoperator n-ter Ordnung
Hierzu sei eine Lösung u der homogenen linearen Differentialgleichung
bekannt. Für
gilt dann
Mit anderen Worten:
 löst die inhomogene Differentialgleichung n-ter Ordnung
löst die inhomogene Differentialgleichung n-ter Ordnung 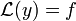 genau dann, wenn
genau dann, wenndie inhomogene lineare Differentialgleichung (n − 1)-ter Ordnung
löst.
Beweis
Nach der leibnizschen Regel gilt
also
Nun ist nach Voraussetzung
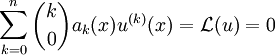 . Somit folgt
. Somit folgtIndexverschiebung liefert
![\mathcal{L}(y) = \sum_{j=0}^{n-1}\left[\sum_{k=j+1}^n{k \choose {j+1}}a_k(x)u^{(k-j-1)}(x)\right]c^{(j+1)}(x)](/pictures/dewiki/49/1b556934bd60cbd347584f81a5b7ceb3.png) .
.
Spezialfall: Lineare Differentialgleichung zweiter Ordnung
Sei u Lösung der homogenen linearen Differentialgleichung zweiter Ordnung
Dann ist
Lösung der (inhomogenen) Differentialgleichung
genau dann, wenn
der Gleichung
genügt. Diese Gleichung lässt sich mit Hilfe der Variation der Konstanten vollständig lösen.
Wikimedia Foundation.

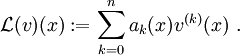
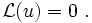
![\mathcal{L}(y)(x) = \sum_{j=0}^{n-1}\left[\sum_{k=j+1}^n{k \choose {j+1}}a_k(x)u^{(k-j-1)}(x)\right]c^{(j+1)}(x)\ .](/pictures/dewiki/52/45cf77b37a6247ef25b38f96e2a3d9ce.png)
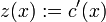
![\sum_{j=0}^{n-1}\left[\sum_{k=j+1}^n{k \choose {j+1}}a_k(x)u^{(k-j-1)}(x)\right]z^{(j)}(x) = f(x)](/pictures/dewiki/57/9eb522dad876cb37b6a8a17c9825d390.png)
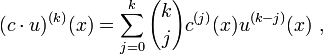
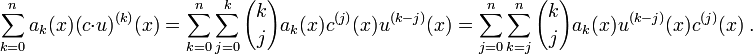
![\mathcal{L}(y) = \sum_{k=0}^na_k(x)(c\cdot u)^{(k)}(x) = \sum_{j=1}^n\left[\sum_{k=j}^n{k \choose j}a_k(x)u^{(k-j)}(x)\right]c^{(j)}(x)\ .](/pictures/dewiki/49/13db0039ae529e4937141bfe844a3c64.png)
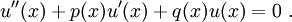
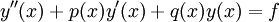
![\ u(x)z'(x) + [p(x)u(x) + 2u'(x)]z(x) = f(x)](/pictures/dewiki/50/2fd5e1abe3092e4188cfd4d7bb905fc3.png)