- Hauptvektorlösung
-
Als Fundamentalsystem bezeichnet man in der Analysis jede Basis des Vektorraums, der aus der Menge der Lösungen eines homogenen linearen gewöhnlichen Differentialgleichungssystems gebildet wird.
Ist
 ein Fundamentalsystem, so ist definitionsgemäß
ein Fundamentalsystem, so ist definitionsgemäßdie Menge der Lösungen dieses homogenen Differentialgleichungssystems.
Die Kenntnis eines Fundamentalsystems ist Voraussetzung für das Verfahren der Variation der Konstanten, um eine spezielle Lösung von inhomogenen linearen Differentialgleichungssystemen erster Ordnung bzw. inhomogenen linearen Differentialgleichungen höherer Ordnung zu konstruieren.
Fundamentalsystem, (Haupt-)Fundamentalmatrix und Wronski-Determinante
Homogenes lineares Differentialgleichungssystem erster Ordnung
Gegeben sei ein lineares homogenes Differentialgleichungssystem erster Ordnung
Die Koeffizientenmatrix
![A:[a,b]\to\R^{n\times n}](/pictures/dewiki/101/e879aa78c93c8d6eaa891adeff21e4d2.png) ist dabei eine matrixwertige Funktion. Die Lösungen dieses Differentialgleichungssystems werden im Raum
ist dabei eine matrixwertige Funktion. Die Lösungen dieses Differentialgleichungssystems werden im Raum ![C^1([a,b];\R^n)](/pictures/dewiki/100/d2de0dad98a82f7f31647189b4925505.png) der stetig differenzierbaren Funktionen
der stetig differenzierbaren Funktionen ![y:[a,b]\to\R^{n}](/pictures/dewiki/56/8556957fdcd8cec30dd050b75689c581.png) gesucht.
gesucht.Hat diese Differentialgleichung zwei verschiedene Lösungen, so sind auch die Summe und Vielfache mit reellen Faktoren wiederum Lösungen. Die Lösungsmenge ist also ein reeller Unterraum im Raum aller stetig differenzierbaren Funktionen.
Ist die Koeffizientenmatrix A eine stetige matrixwertige Funktion, so kann der Existenz- und Eindeutigkeitssatz von Picard-Lindelöf angewandt werden und nach diesem ist jede Lösung der Differentialgleichung schon eindeutig durch ihren Wert y(a) im Anfangspunkt des Intervalls eindeutig bestimmt. Andererseits ist auch jedes Anfangswertproblem mit beliebigem Anfangswert
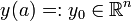 zu diesem Differentialgleichungssystem eindeutig lösbar. Daraus folgt, dass der Raum der Lösungen n-dimensional ist.
zu diesem Differentialgleichungssystem eindeutig lösbar. Daraus folgt, dass der Raum der Lösungen n-dimensional ist.Definitionen
Jede Basis dieses n-dimensionalen Lösungsraums wird als Fundamentalsystem des linearen Differentialgleichungssystems bezeichnet. Meistens wählt man als Basis dasjenige System von Lösungsfunktionen
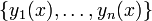 , für welche der Anfangswert yi(a) = ei der i-te kanonische Einheitsvektor ist.
, für welche der Anfangswert yi(a) = ei der i-te kanonische Einheitsvektor ist.Ist
 ein Fundamentalsystem, so bezeichnet man die Matrix
ein Fundamentalsystem, so bezeichnet man die Matrix 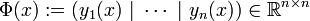 als Fundamentalmatrix (manchmal auch als Wronski-Matrix) und ihre Determinante
als Fundamentalmatrix (manchmal auch als Wronski-Matrix) und ihre Determinante 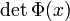 als Wronski-Determinante. Ist Φ(x0) für ein x0 die Einheitsmatrix, so bezeichnet man Φ auch als Hauptfundamentalmatrix im Punkt x0.
als Wronski-Determinante. Ist Φ(x0) für ein x0 die Einheitsmatrix, so bezeichnet man Φ auch als Hauptfundamentalmatrix im Punkt x0.Die Fundamentalmatrix Φ ist ebenfalls Lösung einer homogenen gewöhnlichen (matrixwertigen) Differentialgleichung, nämlich von
Der Lösungsraum des ursprünglichen homogenen Systems im
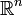 ist dann
ist dann ![\{y \in C^1([a,b]; \mathbb{R}^n)\ |\ y(x)=\Phi(x)\cdot c,\ c \in \mathbb{R}^n\}](/pictures/dewiki/50/295112515e8e052905c942cd13d42e3d.png) . Ist Φ sogar Hauptfundamentalmatrix in x0, so löst y(x): = Φ(x)y0 das Anfangswertproblem zu y(x0) = y0.
. Ist Φ sogar Hauptfundamentalmatrix in x0, so löst y(x): = Φ(x)y0 das Anfangswertproblem zu y(x0) = y0.Die Fundamentalmatrix
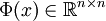 ist für jedes
ist für jedes ![x\in[a,b]](/pictures/dewiki/56/8290bddba5acf9822dcbf61f4ac67d1b.png) invertierbar. Für die Wronski-Determinante gilt die liouvillesche Formel.
invertierbar. Für die Wronski-Determinante gilt die liouvillesche Formel.Homogene lineare Differentialgleichung höherer Ordnung
Genauso wie im Fall erster Ordnung ist der Lösungsraum eines linearen Systems höherer Ordnung ebenfalls ein Vektorraum, und jede Basis dessen wird weiterhin als Fundamentalsystem bezeichnet.
Zur Definition der Fundamentalmatrix einer skalaren linearen Differentialgleichung n-ter Ordnung
betrachte man zunächst das hierzu korrespondierende Differentialgleichungssystem erster Ordnung, bestehend aus n Gleichungen
- Y'(x) = A(x)Y(x) mit
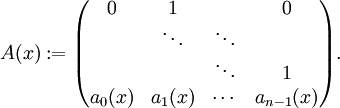
[Der Zusammenhang ist folgender: y(x) löst die skalare Gleichung n-ter Ordnung genau dann, wenn
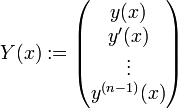 Lösung obigen Systems erster Ordnung ist.]
Lösung obigen Systems erster Ordnung ist.]Als Fundamentalmatrix (Wronski-Matrix) von
bezeichnet man jede Fundamentalmatrix Φ des Systems erster Ordnung
Natürlich heißt Φ Hauptfundamentalmatrix in x0, falls Φ(x0) die Einheitsmatrix ist. detΦ bezeichnet man weiterhin als Wronski-Determinante.
Obige Reduktion der Gleichung auf ein System erster Ordnung liefert: Ist
 ein Fundamentalsystem, so ist
ein Fundamentalsystem, so isteine Fundamentalmatrix.
Konstruktion eines Fundamentalsystems
Im allgemeinen Fall ist es schwierig, Fundamentalsysteme zu konstruieren. Möglich wird dies erst durch eine spezielle Struktur der Differentialgleichung. Dazu gehört die skalare Differentialgleichung erster Ordnung, Differentialgleichungssysteme erster Ordnung mit konstanten Koeffizienten, Differentialgleichungen höherer Ordnung mit konstanten Koeffizienten oder die eulersche Differentialgleichung. Ist a priori die Lösung einer homogenen Differentialgleichung hoher Ordnung bekannt, so kann man das Reduktionsverfahren von d'Alembert verwenden, um die Gleichung auf eine Differentialgleichung mit einer um eins erniedrigten Ordnung zurückzuführen.
Lineare Differentialgleichung erster Ordnung
Es sei A eine Stammfunktion von a. Dann ist
ein Fundamentalsystem von y'(x) = a(x)y(x).
Lineares Differentialgleichungssystem erster Ordnung mit konstanten Koeffizienten
Im Fall einer linearen Differentialgleichung mit konstanten Koeffizienten
bestimmt man zunächst die Jordan-Normalform J der Matrix A sowie eine dazugehörige Jordan-Basis
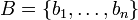 . Ist λ ein komplexer Eigenwert mit zugehörigen Basisvektoren
. Ist λ ein komplexer Eigenwert mit zugehörigen Basisvektoren 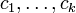 , so möge man in der Jordan-Basis die Basisvektoren so wählen, dass
, so möge man in der Jordan-Basis die Basisvektoren so wählen, dass 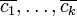 als Basisvektoren zu
als Basisvektoren zu  vorkommen.
vorkommen.Nun geht man jede Kette von Hauptvektoren einzeln durch: Ist
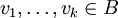 eine (vollständige) Hauptvektorkette zum Eigenwert λ, d. h.
eine (vollständige) Hauptvektorkette zum Eigenwert λ, d. h.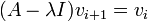 ,
,
so tragen sie zum Fundamentalsystem die k (Hauptvektor-)Lösungen
allgemein
bei. Nachdem man alle Hauptvektorketten durchgegangen ist, hat man dann ein (ggf. komplexes) Fundamentalsystem aufgestellt.
Lineare Differentialgleichung höherer Ordnung mit konstanten Koeffizienten
Zur skalaren linearen Differentialgleichung n-ter Ordnung mit konstanten Koeffizienten
stelle man das charakteristische Polynom
auf. Seien
 seine (paarweise verschiedenen) Nullstellen mit Vielfachheit
seine (paarweise verschiedenen) Nullstellen mit Vielfachheit  . Dann trägt der Eigenwert λi zum (komplexen) Fundamentalsystem die μi Basisvektoren
. Dann trägt der Eigenwert λi zum (komplexen) Fundamentalsystem die μi Basisvektorenbei.
[Zur Erläuterung der Sprechweise: Führt man mit Hilfe der obigen Transformation die skalare Gleichung n-ter Ordnung auf ein Differentialgleichungssystem erster Ordnung zurück, so hat die Koeffizientenmatrix als charakteristisches Polynom genau dieses, welches hier angegeben wurde.]
Reelles Fundamentalsystem
Im Falle komplexer Nullstellen des charakteristischen Polynoms erhält man auf obige Weise n linear unabhängige Lösungen, welche aber teilweise komplexwertig sind - die komplexen Lösungen kommen jedoch immer in konjugiert komplexen Paaren vor, da die Differentialgleichung reell war. Nun sind mit y(x) auch
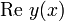 und
und 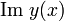 beides (reelle) Lösungen, da die Differentialgleichung linear ist. Man ersetze daher jedes Paar komplex konjugierter Lösungen
beides (reelle) Lösungen, da die Differentialgleichung linear ist. Man ersetze daher jedes Paar komplex konjugierter Lösungen 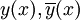 im (komplexen) Fundamentalsystem durch
im (komplexen) Fundamentalsystem durch 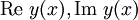 . Auf diese Weise erhält man ein (reelles) Fundamentalsystem. Man beachte hierbei die eulersche Identität eix = cosx + isinx.
. Auf diese Weise erhält man ein (reelles) Fundamentalsystem. Man beachte hierbei die eulersche Identität eix = cosx + isinx.Periodisches Differentialgleichungssystem erster Ordnung
Für das System
mit ω-periodischer stetiger Koeffizientenmatrix
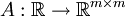 kann man zwar nicht explizit ein Fundamentalsystem konstruieren - jedoch macht der Satz von Floquet eine Aussage über die Struktur der Fundamentalmatrizen dieses Systems.
kann man zwar nicht explizit ein Fundamentalsystem konstruieren - jedoch macht der Satz von Floquet eine Aussage über die Struktur der Fundamentalmatrizen dieses Systems.Beispiele
Lineares Differentialgleichungssystem erster Ordnung mit konstanten Koeffizienten
Man betrachte das Differentialgleichungssystem
Die Matrix A besitzt 1 als einfachen Eigenwert und 2 als doppelten Eigenwert. Ihre Eigenräume lauten
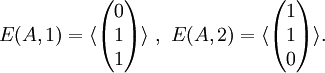 Für die Hauptvektorkette zum Eigenwert 2 benötigt man noch
Für die Hauptvektorkette zum Eigenwert 2 benötigt man nochWähle beispielsweise
Dann muss als Hauptvektor erster Stufe
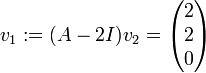 gewählt werden. Es ergibt sich als Fundamentalsystem {y1,y2,y3} mit
gewählt werden. Es ergibt sich als Fundamentalsystem {y1,y2,y3} mitLineare Differentialgleichung höherer Ordnung mit konstanten Koeffizienten
Betrachte nun
- y(4)(x) − y(x) = 0.
Diese Differentialgleichung hat als charakteristisches Polynom λ4 − 1, welches die vier Nullstellen 1, − 1,i, − i besitzt. Daher erhält man zunächst als komplexes Fundamentalsystem
- {ex,e − x,eix,e − ix}.
Somit erhält man als ein reelles Fundamentalsystem
- {ex,e − x,sinx,cosx}.
Literatur
- Carmen Chicone: Ordinary Differential Equations with Applications. 2. Auflage. Texts in Applied Mathematics 34, Springer-Verlag 2006, ISBN 0-387-30769-9.
Wikimedia Foundation.

![\{y \in C^1([a,b]; \mathbb{R}^n)\ |\ y = \sum_{k=1}^na_ky_k\ ,\ a_1, \ldots, a_n \in \mathbb{R}\}](/pictures/dewiki/50/206c5e27d8e4dbd5fbb9be9db982a670.png)
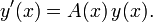
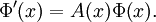
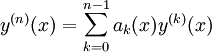
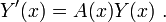
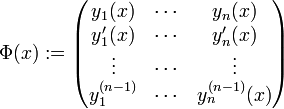
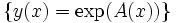
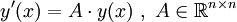

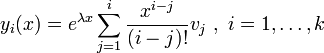

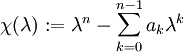
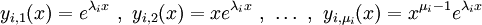
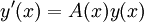
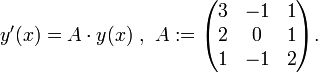
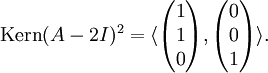
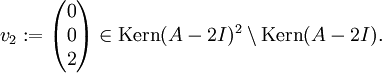
![y_1(x) := e^x\cdot\begin{pmatrix}0\\1\\1\\\end{pmatrix}\ ,\
y_2(x) := e^{2x}\cdot\begin{pmatrix}2\\2\\0\\\end{pmatrix}\ ,\
y_3(x) := e^{2x}\cdot\left[\begin{pmatrix}2x\\2x\\0\\\end{pmatrix} +
\begin{pmatrix}0\\0\\2\\\end{pmatrix}\right]\ .](/pictures/dewiki/101/e9a457727dda9a0a1f745ea6cb978b7d.png)