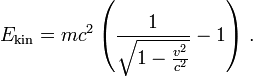Relativitätstheorie (Geschichte)

Relativitätstheorie (Geschichte)

Unter der Geschichte der speziellen Relativitätstheorie versteht man die Entwicklung von empirischen und konzeptionellen Vorschlägen und Erkenntnissen innerhalb der theoretischen Physik. Diese Entwicklung wurde insbesondere von Hendrik Antoon Lorentz und Henri Poincaré eingeleitet und gipfelte 1905 in der Ausarbeitung der speziellen Relativitätstheorie (SRT) durch Albert Einstein. In der Folge wurde die Theorie weiter ausgebaut, vor allem durch Hermann Minkowski.

Überblick

Isaac Newton war in seinen 1687 publizierten Principia von einem absoluten Raum und einer absoluten Zeit ausgegangen. Gleichwohl galt auch in seiner Theorie das Relativitätsprinzip von Galileo Galilei, wonach alle relativ zueinander gleichförmig bewegten Beobachter ihren absoluten Bewegungszustand nicht bestimmen können. Ihre Perspektiven sind demnach gleichberechtigt und der Galilei-Transformation unterworfen; es gibt kein privilegiertes Bezugssystem. Ende des 19. Jahrhunderts betonten verschiedene Physiker, genau genommen führe dies zu einer Vervielfältigung „absoluter Räume“ – so etwa Ludwig Lange, der 1885 den operational begründeten Begriff Inertialsystem einführte. Ernst Mach sah die Absolutheit von Raum und Zeit nicht hinreichend phänomenologisch-empirisch fundiert.[1]

Das Gegenstück zum „absoluten Raum“ der Mechanik war der Äther in der Elektrodynamik. Gemäß einer im 19. Jahrhundert allgemein geltenden Voraussetzung brauchen Wellen ein Ausbreitungsmedium: wie der Schall die Luft braucht, so das Licht den Äther, der – ähnlich der Luft – als stofflich vorgestellt wurde. James Clerk Maxwell hatte diese Voraussetzung so formuliert, dass sich alle optischen und elektrischen Phänomene in einem Medium ausbreiten. Unter diesen Vorannahmen hat die Lichtgeschwindigkeit den durch die maxwellschen Gleichungen angegebenen Wert nur relativ zum Äther. Unter der damals weit verbreiteten Voraussetzung, dass der Äther ruht und nicht von der Erde mitgeführt wird, wäre es möglich, den Bewegungszustand der Erde relativ zum Äther zu bestimmen und diesen somit als ein ausgezeichnetes Bezugssystem zu verwenden. Allerdings scheiterten alle Versuche, die Relativbewegung der Erde zu ihm zu bestimmen.[2]

Dies führte ab 1892 zur Entwicklung der maxwell-lorentzschen Elektrodynamik durch Hendrik Antoon Lorentz, welche auf einem absolut ruhenden Äther beruhte. Dessen Unauffindbarkeit wurde durch die Annahmen erklärt, dass im Äther bewegte Körper verkürzt sind (Längenkontraktion), und Prozesse bei im Äther bewegten Körpern verlangsamt ablaufen (Zeitdilatation). Grundlage dafür war jedoch, dass die Galilei-Transformation durch die Lorentz-Transformation ersetzt wurde. Lorentz konnte in seiner nachfolgenden Arbeit von 1904 das Relativitätsprinzip jedoch nur unvollkommen erfüllen.[3] Henri Poincaré erkannte 1904, dass die Unüberschreitbarkeit der Lichtgeschwindigkeit für alle Beobachter das Hauptmerkmal der „neuen Mechanik“ (also der lorentzschen Theorie) war. 1905 gelang ihm eine vollständige physikalische Verallgemeinerung und mathematisch elegante Formalisierung der lorentzschen Elektrodynamik, wobei er das Relativitätsprinzip als universell gültiges Naturgesetz einschließlich der Elektrodynamik und Gravitation festlegte – jedoch hielt er weiterhin an der Existenz eines Äthers und der Unterscheidung zwischen „wahren“ und „scheinbaren“ Längen und Zeiten fest.

Albert Einstein gelang 1905 mit der speziellen Relativitätstheorie (SRT) schließlich durch Wandlung der Begriffe von Raum und Zeit und durch Abschaffung des Äthers eine völlige Neuinterpretation der lorentzschen Elektrodynamik.[4] Diese Ergebnisse leitete Einstein ausschließlich aus dem Relativitätsprinzip und dem Prinzip der Konstanz der Lichtgeschwindigkeit, die er als Postulate seiner Theorie zugrundelegte, ab. Durch die Abschaffung der Konzeption eines Äthers gab es nun keinen Grund mehr für eine Unterscheidung zwischen „wahren“ und „scheinbaren“ Koordinaten, wie noch bei Poincaré und Lorentz. Dies alles machte den Weg zu relativistischen Feldtheorien und zur Entwicklung der allgemeinen Relativitätstheorie (ART) frei. Die Untersuchungen zur SRT wurden nach Einstein unter anderem durch Hermann Minkowski fortgesetzt, der 1907 die formalen Grundlagen für das heute übliche Konzept der vierdimensionalen Raumzeit entwickelte.

Inhaltsverzeichnis


Vorgeschichte

Elektrodynamik und Ätherwind

Äthermodelle und Maxwellsche Gleichungen

Im 19. Jahrhundert war man vor allem durch die Arbeiten von Thomas Young (1804) und Augustin Jean Fresnel (1816) zur Überzeugung gelangt, dass Licht sich als eine Transversalwelle in einem Medium („Lichtäther“) ausbreitet, welches von vielen als ein elastischer Festkörper aufgefasst wurde. Es wurde jedoch weiterhin zwischen optischen Phänomenen einerseits, elektrodynamischen andererseits unterschieden. Das heißt, es mussten für diese Phänomene jeweils eigene Äthervarianten konstruiert werden. Versuche, diese Äthervarianten zu vereinigen und eine vollständig gültige mechanische Beschreibung des Äthers vorzulegen, scheiterten jedoch.[5]

James Clerk Maxwell

Nach Vorarbeiten von Physikern wie Michael Faraday, Lord Kelvin und anderen entwickelte James Clerk Maxwell (1864) nun grundlegende Gleichungen für Elektrizität und Magnetismus, die so genannten maxwellschen Gleichungen. Dabei entwarf er ein Modell, in dem die Phänomene der Optik als auch der Elektrodynamik zusammen auf einen einzigen, elektromagnetischen Äther zurückzuführen sind, und definierte Licht als eine elektromagnetische Welle, welche sich konstant mit Lichtgeschwindigkeit in Bezug zum Äther ausbreitete.[6] Als weitere wichtige Konsequenz der Theorie wurde von Maxwell (1873) die Existenz von elektrostatischen und magnetischen „Spannungen“ abgeleitet, die einen Druck auf Körper ausüben können − eine unmittelbare Folge davon ist der vom Licht ausgeübte Strahlungsdruck. Adolfo Bartoli (1876) leitete die Existenz desselben Drucks aus thermodynamischen Überlegungen ab.[7]

Joseph John Thomson (1881) erkannte während seiner Weiterentwicklung der maxwellschen Elektrodynamik, dass elektrostatische Felder sich so verhalten, als ob sie den Körpern neben der mechanischen eine „elektromagnetische Masse“ hinzufügen würden. Dies wurde damals als das Ergebnis einer Selbstinduktion der Konvektionsströme im Äther interpretiert. Er erkannte auch, dass diese Masse bei bewegten Körpern (um einen allerdings für alle Geschwindigkeiten > 0 gleichen Faktor) größer wird. [8][9] Vor allem George FitzGerald, Oliver Heaviside, und George Frederick Charles Searle korrigierten einige Fehler und führten die Arbeit von Thomson fort - wobei als Ausdruck für die elektromagnetische Masse sich die Formel (in moderner Notation) m = (4 / 3)E / c2 ergab. Heaviside (1888) erkannte überdies, dass die Zunahme der elektromagnetischen Masse bei bewegten Körpern keineswegs konstant ist, sondern bei größerer Geschwindigkeit immer weiter zunimmt. Searle (1897) folgerte daraus, dass dies ein Überschreiten der Lichtgeschwindigkeit unmöglich macht, da unendlich viel Energie dafür erforderlich wäre. In denselben Arbeiten stellten Heaviside und Searle überdies fest, dass elektrostatische Felder in Bewegungsrichtung kontrahiert waren (Heaviside-Ellipsoid).[10]

Nachdem Heinrich Hertz (1887) die Existenz von elektromagnetischen Wellen nachgewiesen hatte, wurde die maxwellsche Theorie schließlich weithin akzeptiert. Heaviside (1889) und Hertz (1890) führten dabei modernisierte Versionen der maxwellschen Gleichungen ein, welche eine wichtige Grundlage für die weitere Entwicklung der Elektrodynamik bildeten („maxwell-hertzsche“ bzw. „heaviside-hertzsche“ Gleichungen). Dabei war es schließlich die von Heaviside gegebene Form, welche sich allgemein durchsetzte. Anfang 1900 wurde die hertzsche Theorie jedoch experimentell widerlegt und musste aufgegeben werden.[11][12] Hertz selbst war dabei einer der letzten Anhänger des „mechanistischen Weltbildes“, wonach alle elektromagnetischen Prozesse auf mechanische Stoß- und Kontaktwirkungen im Äther zurückgeführt werden sollten.[13]

Unauffindbarkeit des Äthers

Was nun den Bewegungszustand des Äthers relativ zur Materie betraf, wurden prinzipiell zwei Möglichkeiten in Betracht gezogen, welche bereits vor den Arbeiten Maxwells diskutiert wurden:

  1. die von Fresnel (1818) und später von Hendrik Antoon Lorentz (1892a) vertretene Vorstellung eines ruhenden bzw. nur teilweise mit einem bestimmten Koeffizienten mitgeführten Äther,[14] und
  2. die von George Gabriel Stokes (1845) und später von Hertz (1890) angenommene vollständige Mitführung des Äthers durch die Materie.[15]

Fresnels Theorie wurde bevorzugt, weil mit seiner Theorie die Aberration des Lichtes und viele optische Phänomene erklärt werden konnten und weil sein Mitführungskoeffizient von Hippolyte Fizeau (1851) mit dem Fizeau-Experiment sehr genau gemessen wurde. Hingegen die Theorie von Stokes konnte sich nicht durchsetzen, da sie sowohl der Aberration als auch dem Ergebnis des Fizeau-Experiments widersprach − die deswegen eingeführten Hilfshypothesen waren nicht überzeugend oder überhaupt widersprüchlich.[16]

Albert Abraham Michelson

Albert Abraham Michelson (1881) versuchte die Relativbewegung von Erde und Äther („Ätherwind“), welche nach Fresnels Theorie hätte auftreten müssen, direkt zu messen. Er konnte jedoch mit seiner Interferometeranordnung das von ihm erwartete Ergebnis nicht feststellen und interpretierte das Ergebnis als Beleg für die These von Stokes (vollständige Äthermitführung durch die Erde) und damit gegen die Theorie Fresnels.[17] Lorentz (1886) wies jedoch nach, dass Michelson bei den Berechnungen ein Rechenfehler unterlaufen war, woraus sich ergab, dass das Experiment zu ungenau war, um im Rahmen der Messgenauigkeit überhaupt ein positives Messresultat zu erbringen, was von Michelson selbst zugegeben wurde.[18] Da die fresnelsche Theorie nun doch nicht widerlegt schien, führten Michelson und Edward Morley (1886) ein Experiment durch, bei dem die Messungen Fizeaus zum fresnelschen Mitführungskoeffizienten überprüft werden sollten. Tatsächlich gelang die Bestätigung und entgegen seiner Aussage von 1881 war Michelson diesmal der Meinung, dass damit der ruhende Äther Fresnels bestätigt sei.[19] Dies erforderte allerdings eine Wiederholung des Michelson-Experiments von 1881, wobei zur großen Überraschung von Michelson und Morley dieses heute berühmte Michelson-Morley-Experiment das erwartete positive Resultat abermals nicht lieferte. Wieder schien das Experiment den eigentlich bereits widerlegten stokeschen Äther zu bestätigen und stand im krassen Gegensatz zu dem Versuch von 1886, welcher für den fresnelschen Äther sprach.[20]

Woldemar Voigt entwickelte (1887) auf Basis eines elastischen Äthermodells (also nicht des elektromagnetischen Modells Maxwells) und im Zuge von Untersuchungen zum Dopplereffekt eine Koordinatentransformation zwischen einem im Äther ruhenden und einem bewegten System. Die Gleichungen der Voigt-Transformation ließen die Wellengleichung unverändert, waren bis auf einen unterschiedlichen Skalenfaktor identisch mit der späteren Lorentz-Transformation und konnten den Michelson-Morley-Versuch erklären. Dabei beinhalteten sie den später als „Lorentz-Faktor“ bekannten Ausdruck 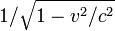1/\sqrt{1-v^{2}/c^{2}} für die y- und z-Koordinaten und eine später als Ortszeit benannte neue Zeitvariable t' = t − vx / c2. Sie waren allerdings nicht symmetrisch und verletzten folglich das Relativitätsprinzip. Diese Arbeit Voigts wurde von seinen Zeitgenossen völlig ignoriert.[21][22]

Den Arbeiten Heavisides zur Kontraktion elektrostatischer Felder folgend führte George FitzGerald (1889) die Ad-hoc-Hypothese ein, dass auch materielle Körper in Bewegungsrichtung kontrahieren, was zur Längenkontraktion führt und den Michelson-Morley-Versuch erklären könnte − im Gegensatz zu Voigts Gleichungen wird hier also die x-Koordinate verändert. Fitzgerald begründete dies damit, dass die intermolekularen Kräfte möglicherweise elektrischen Ursprungs seien. Jedoch wurde seine Idee vorerst nicht zur Kenntnis genommen und erst durch eine Veröffentlichung von Oliver Lodge (1892) bekannt.[23] Unabhängig von Fitzgerald schlug auch Lorentz (1892b) dieselbe Hypothese vor („Fitzgerald-Lorentzsche Kontraktionshypothese“). Aus Plausibilitätsgründen verwies er wie Fitzgerald auf die Analogie zur Kontraktion der elektrostatischen Felder, wobei er jedoch selbst zugab, dass das keine zwingende Begründung war.[24][25]

Elektronentheorien

Theorie von Lorentz

Hendrik Antoon Lorentz

Hendrik Antoon Lorentz (1892a) legte die Fundamente der (maxwell-)lorentzschen Elektrodynamik bzw. Äther- oder Elektronentheorie, indem er wie andere vor ihm neben dem Äther auch die Existenz von Elektronen annahm. Dabei ging er davon aus, dass der Äther vollständig in Ruhe sei und nicht von den Elektronen mitgeführt wird. Daraus ergab sich die wichtige Konsequenz, dass die Lichtgeschwindigkeit vollständig unabhängig von der Geschwindigkeit der Lichtquelle ist und folglich relativ zu einem Koordinatensystem, in dem der Äther ruht, unter allen Umständen konstant ist. Statt dabei irgendwelche Aussagen über die mechanische Natur des Äthers und der elektromagnetischen Prozesse zu machen, versuchte er umgekehrt, viele mechanische Prozesse auf elektromagnetische zurückzuführen. Im Rahmen seiner Theorie errechnete Lorentz (wie Heaviside) die Kontraktion der elektrostatischen Felder und führte dazu, unabhängig von Voigt, als mathematische Hilfsvariable die Ortszeit ein. Somit verfügte er über eine Vorform der später als Lorentz-Transformation bekannten Gleichungen, welche zur Erklärung aller negativen Ätherdriftexperimente für Größen erster Ordnung von v/c diente. Dabei verwendete er (1895) den Begriff „Theorem der korrespondierenden Zustände“, d. h. die Lorentz-Kovarianz der elektromagnetischen Gleichungen für relativ geringe Geschwindigkeiten. Daraus folgt, dass die Form der elektromagnetischen Gleichungen eines „realen“ - im Äther ruhenden - Systems der Form eines „fiktiven“ - im Äther bewegten - Systems entspricht. Jedoch erkannte Lorentz, dass seine Theorie gegen das Prinzip von actio und reactio verstieß, da zwar der Äther auf die Materie wirken, jedoch die Materie nicht auf den Äther zurückwirken konnte.[26]

Joseph Larmor (1897, 1900) entwarf ein sehr ähnliches Modell wie Lorentz, jedoch ging er einen Schritt weiter und brachte die Lorentz-Transformation in eine algebraisch äquivalente Form, wie sie bis heute benutzt wird. Dabei sah er, dass nicht nur die Längenkontraktion daraus abgeleitet werden kann, sondern er berechnete auch eine Art Zeitdilatation, wonach Rotationen von im Äther bewegten Elektronen langsamer ablaufen als bei ruhenden Elektronen.[27] Larmor konnte jedoch nur zeigen, dass diese Transformation zwar für Größen zweiter Ordnung, nicht jedoch für alle Ordnungen gültig ist. Auch Lorentz (1899) erweiterte seine Transformation für Größen zweiter Ordnung (mit einem allerdings unbestimmten Faktor) und vermerkte, wie Larmor zuvor, eine Art Zeitdilatation. Besonders wichtig in seiner Theorie war die Integrierung der u. a. von Thomson erkannten Geschwindigkeitsabhängigkeit der Massen. Er bemerkte, dass diese aufgrund der Lorentz-Transformation nicht nur mit der Geschwindigkeit, sondern auch mit der Richtung variiert und führte die später von Max Abraham als longitudinale und transversale Masse bekannt gewordenen Terme ein – wobei nur die transversale Masse dem später als relativistische Masse bezeichneten Begriff entsprach.[28] In einer anderen Schrift bekräftige Lorentz den rein formalen Charakter der Ortszeit und betonte, dass man sich darunter keine physikalische Zeit vorstellen soll.[29] Unbekannt ist, inwiefern sich Lorentz und Larmor gegenseitig beeinflusst haben; das heißt, es ist nicht klar, ob Larmor (1897) die Ortszeit von Lorentz übernommen hat, und ob umgekehrt Lorentz (1899) die vollständigen Transformationen von Larmor übernommen hat. Beide zitieren zwar die Werke des anderen und standen in brieflichem Kontakt, jedoch diskutierten sie nicht über die Lorentz-Transformation.[22]

Wilhelm Wien (1900) (und vor ihm schon Larmor und Emil Wiechert) vertrat auf Basis der Theorie von Lorentz die Ansicht, dass - entgegen dem „mechanistischen Weltbild“ von Hertz - sämtliche Kräfte der Natur elektromagnetisch erklärbar seien („elektromagnetisches Weltbild“).[30]. Entsprechend nahm er an, dass die gesamte Masse elektromagnetischen Ursprungs sei. Das heißt, für Wien galt die Formel m = (4 / 3)E / c2 – die Thomson (darin Heaviside und Searle folgend) verwendete – für die gesamte Masse der Materie. Auch vermerkte er, dass die Gravitation der elektromagnetischen Energie proportional sein müsse, falls sie ebenfalls auf elektromagnetische Energie zurückgeführt werden könnte.

Henri Poincaré (1900b) leitete aus den oben erwähnten maxwellschen Spannungen und der Theorie von Lorentz den elektromagnetischen Impuls ab und folgerte in Verbindung mit dem Reaktionsprinzip, dass die elektromagnetische Energie einer „fiktiven“ Masse von m = E / c2 bzw. E = mc2 entsprach – wobei Poincaré diese Begriffe als mathematische Fiktionen ansah. Er stieß dabei jedoch auf ein Strahlungsparadoxon, welches erst später von Einstein befriedigend gelöst wurde.[31]

Emil Cohn (1900) entwarf eine alternative Elektrodynamik, wobei er als einer der Ersten die Existenz des Äthers (zumindest in bisheriger Form) verwarf und stattdessen, wie Ernst Mach, die Fixsterne als Bezugskörper verwendete. So konnte er zwar das Michelson-Morley-Experiment erklären, da die Erde relativ zu den Fixsternen in Ruhe ist, jedoch konnte nach seiner Theorie die Lichtgeschwindigkeit in Medien gleichzeitig in verschiedenen Richtungen überschritten werden. Wegen dieser und anderer Unstimmigkeiten wurde die Theorie (auch von Cohn selbst) später verworfen. Darüber hinaus diskutierte er auch die Theorie von Lorentz und verwendete den Begriff „Lorentz'sche Transformation“.[32]

Dynamik des Elektrons

Aus den Arbeiten von Searle, Lorentz und anderen ergab sich also eine Abhängigkeit der Elektronenmasse von der Geschwindigkeit. Walter Kaufmann (1901-1903) war der Erste, der dies experimentell bestätigte. Dabei wurde ein Kathodenstrahl von Elektronen aus Metallen erzeugt, so dass Verhältnisse von Ladung, Geschwindigkeit und Masse bestimmbar wurden. Da vorher schon bekannt war, dass die Ladung eines Elektrons von seiner Geschwindigkeit unabhängig ist, konnte das von Kaufmann experimentell gezeigte Ergebnis einer Abnahme des Ladungs-Masse-Verhältnisses für Geschwindigkeiten nahe der Lichtgeschwindigkeit nur auf eine Massenzunahme der untersuchten Elektronen zurückgeführt werden. Dabei glaubte Kaufmann, dass seine Messungen bewiesen hätten, dass die gesamte Masse der Materie elektromagnetischen Ursprungs sei.[33]

Max Abraham (1902-1903), der wie Wien ein überzeugter Anhänger des elektromagnetischen Weltbildes war, legte dazu eine Erklärung vor und führte die von Lorentz begonnene Theorie fort. So war er der Erste, der ein feldtheoretisches Konzept der Elektronen vorlegte. Im Gegensatz zu Lorentz definierte er das Elektron jedoch als starres, kugelförmiges Gebilde und lehnte deren Kontraktion ab, weshalb auch seine Massen-Terme von den von Lorentz gebrauchten differierten (wobei Abraham als Erster die Begriffe longitudinale und transversale Masse prägte). Zusätzlich führte er Poincaré folgend den Begriff des „elektromagnetischen Impulses“ ein, welcher proportional zu E / c2 ist. Im Gegensatz zu Poincaré und Lorentz verstand er diesen jedoch als reale physikalische Entität. Abrahams Theorie wurde in den nächsten Jahren das wichtigste Konkurrenzmodell zu der Theorie von Lorentz. Kaufmanns Experimente waren jedoch zu ungenau, um eine Entscheidung zwischen den Theorien herbeizuführen.[34]

Relativitätsprinzip und Lichtkonstanz

Absoluter Raum und absolute Zeit

Newtons Definition des absoluten Raumes und der absoluten Zeit wurde nun von einigen Autoren hinterfragt.[35][36][37] Beispielsweise führte Carl Gottfried Neumann (1870) statt irgendwelchen absoluten Größen einen „Körper Alpha“ ein, der einen starren und fixen Bezugskörper darstellen soll, auf den die inertiale Bewegung bezogen werden kann. Ernst Mach (1883) argumentierte, dass Begriffe wie absoluter Raum und Zeit sinnlos seien und dass nur der Bezug auf relative Bewegung sinnvoll sei. Er meinte auch, dass selbst beschleunigte Bewegung wie Rotation durch Bezug auf „ferne Massen“ relativierbar sei, ohne einen absoluten Raum annehmen zu müssen. Die Argumentation von Neumann wurde von Heinrich Streintz (1883) fortgesetzt. Wenn Messungen durch Gyroskope keine Rotation anzeigen, könne man nach Streintz von einer inertialen Bewegung in Bezug auf einen „Fundamentalkörper“ bzw. ein „Fundamental-Koordinatensystem“ sprechen. Schließlich war Ludwig Lange (1885) der Erste, der von ähnlichen Gedankengängen ausgehend den Begriff Inertialsystem einführte, um damit absolute Größen aus der Kinematik zu entfernen. Er definiert dies als „ein System von der Beschaffenheit, dass mit Bezug darauf die in einem Punkt zusammenlaufenden, stetig beschriebenen Bahnen dreier gleichzeitig von demselben Raumpunkte projizierter und sofort sich überlassener Punkte (die aber nicht in einer Geraden liegen sollen) sämtlich geradlinig sind“.

Auch über die Zeit als eine Vierte Dimension wurde spekuliert.[38][39] Beispielsweise tat dies bereits 1754 Jean d’Alembert in der Encyclopédie, sowie einige Autoren im 19. Jahrhundert wie H. G. Wells in seinem Roman Die Zeitmaschine (1895). Und Menyhért Palágyi (1901) entwickelte ein philosophisches Modell, wonach Raum und Zeit lediglich sprachliche Bezeichnungen für eine in Wirklichkeit einheitliche „Raumzeitform“ sei.[40] Dabei benutzt er für seine „Raumzeitlehre“ die Zeit als vierte Dimension, die bei ihm bereits die Form it (i bezeichnet die imaginäre Einheit) hatte. Jedoch bestand in Palágyis Philosophie kein Zusammenhang zur lorentzschen Ortszeit, denn bei ihm ist die Zeitdimension nicht von der Lichtgeschwindigkeit abhängig. Er verwarf auch jeglichen Zusammenhang mit den bereits vorhandenen Konstruktionen von n-dimensionalen Räumen und der nicht-euklidischen Geometrie. Bezeichnenderweise lehnte Palágyi später (1915) auch die Raumzeit-Konstruktionen von Minkowski und Einstein ab – deswegen urteilte Max Born, dass Palágyis Kritik haltlos sei und seine Theorie nicht viel mit der Relativitätstheorie zu tun habe.[41]

Prinzip der relativen Bewegung und Uhrensynchronisation

Henri Poincaré

In der zweiten Hälfte des 19. Jahrhunderts war man intensiv damit beschäftigt, ein weltweites mit elektrischen Signalen synchronisiertes Uhrennetzwerk aufzubauen, wobei auch bereits die Endlichkeit der Lichtgeschwindigkeit berücksichtigt wurde. Daraus zog Henri Poincaré (1898) folgenreiche Konsequenzen für Philosophie und Physik. Er stellte fest, dass die Synchronisation mit Lichtsignalen eine Bedeutung für die Definition der Gleichzeitigkeit an verschiedenen Orten an sich hatte, und deshalb Definition der Gleichzeitigkeit eine reine, auf Bequemlichkeit beruhende Konvention sei. Dabei argumentierte er, dass die Annahme einer konstanten Lichtgeschwindigkeit in alle Richtungen (z. B. für astronomische Zwecke) als „Postulat“ vorteilhaft sei, um Gesetzen wie dem newtonschen Gravitationsgesetz eine möglichst einfache Form zu geben.[42]

Poincaré erklärte (1895, 1900a), dass er nicht an eine absolute Bewegung bzw. die Entdeckung einer Bewegung gegenüber dem Äther glaube, und nannte diese Auffassung „Prinzip der relativen Bewegung“.[43] Im selben Jahr (1900b) erkannte Poincaré, dass man die lorentzsche Ortszeit dadurch definieren kann, dass zwei Beobachter mit Lichtsignalen ihre Uhren synchronisieren (Poincaré-Einstein-Synchronisation). Wenn sie aufgrund des Relativitätsprinzips davon ausgehen, sich in Ruhe zu befinden, so folgern sie, das Licht sei in beide Richtungen gleich schnell unterwegs. Wären sie hingegen gegenüber dem Äther bewegt, würden sie damit einen Fehler machen und die Uhren könnten nicht synchron sein (Relativität der Gleichzeitigkeit). Somit definierte Poincaré die Ortszeit als etwas, was physikalisch interpretiert und mit Uhren angezeigt werden kann – im klaren Gegensatz zur rein mathematischen Interpretation von Lorentz.[44]

Poincaré (1902) veröffentlichte das philosophische und populärwissenschaftliche Buch „Wissenschaft und Hypothese“, welches u. a. enthielt:

  • Philosophisches über die Relativität von Raum, Zeit und Gleichzeitigkeit;
  • die Ausdrücke „Prinzip der relativen Bewegung“ und „Prinzip der Relativität“;
  • die Meinung, dass der Äther niemals entdeckt werden könne, d. h. die Gültigkeit des Relativitätsprinzips;
  • die mögliche Nichtexistenz des Äthers – allerdings auch Argumente für den Äther;
  • ausführliche Schilderungen über die nichteuklidische Geometrie.

Alfred Bucherer (1903) erklärte wie Poincaré, dass nur noch Relativbewegungen der Körper untereinander, nicht jedoch zum Äther feststellbar sind. Im Gegensatz zu Poincaré zog er daraus jedoch den Schluss, dass der Begriff des Lichtäthers dann überhaupt verworfen werden sollte. Die von Bucherer nachfolgend konstruierte Theorie war jedoch sowohl aus experimentellen als auch inhaltlichen Gründen unbrauchbar - ebenso zog Bucherer trotz Verwerfung des Ätherbegriffs keine Konsequenzen in Bezug zur Relativität von Raum und Zeit.[45]

Die 1904-Theorie von Lorentz

Unter dem Einfluss von Poincarés Forderung nach der Unentdeckbarkeit einer absoluten Bewegung kam Lorentz (1904b) schließlich einer Komplettierung seines Theorems der korrespondierenden Zustände sehr nahe. Er entwickelte ebenso wie Abraham ein feldtheoretisches Konzept der Elektronen, welches jedoch im Gegensatz zu Abraham die Kontraktion der Elektronen und somit das Relativitätsprinzip zu berücksichtigen versuchte. Dadurch konnte er unter Verwendung des elektromagnetischen Impulses das negative Resultat des Trouton-Noble-Experiments erklären, bei dem ein Drehmoment aufgrund des Ätherwindes erwartet worden war. Ein weiterer wichtiger Schritt war, dass er die Gültigkeit der Lorentz-Transformation auf nicht-elektrische Kräfte (sofern diese existieren) ausdehnte. Lorentz gelang es jedoch nicht, die vollständige Lorentz-Kovarianz der elektromagnetischen Gleichungen zu zeigen.[46]

Wien (1903) stellte wie vor ihm Searle (1897) fest, dass aufgrund der Geschwindigkeitsabhängigkeit der Masse eine Überschreitung der Lichtgeschwindigkeit unendlich viel Energie erfordert, also unmöglich ist. Und nachdem ihm die endgültige Fassung von Lorentz’ Theorie vorlag, folgerte er (1904) dasselbe aus der Längenkontraktion, da bei Überlichtgeschwindigkeit die Länge eines Körpers einen imaginären Wert annehmen würde.[47]

Abraham (1904) zeigte jedoch einen wichtigen Defekt in der lorentzschen Theorie auf. Diese Theorie war einerseits so konstruiert, dass das Relativitätsprinzip erfüllt ist, aber auch der elektromagnetische Ursprung aller Kräfte sollte aufgezeigt werden. Abraham zeigte, dass beide Annahmen nicht verträglich sind, da in der lorentzschen Theorie die kontrahierten Elektronen eine nicht-elektrische Bindungsenergie benötigten, die die Stabilität der Materie garantiert. In Abrahams Theorie des starren Elektrons war eine solche Energie nicht notwendig.[48] Es stellte sich nun also die Frage, ob das elektromagnetische Weltbild (verträglich mit Abrahams Theorie) oder das Relativitätsprinzip (verträglich mit Lorentz’ Theorie) korrekt war.[49][50]

Bereits unter Berücksichtigung der neuen Theorie von Lorentz definierte Poincaré (1904) in einer Rede im September in St. Louis (durch Verbindung des galileischen Relativitätsprinzips mit dem lorentzschen Theorem der korrespondierenden Zustände) das „Prinzip der Relativität“ als eine Forderung, dass die Naturgesetze für alle Beobachter die gleichen sein müssen, unabhängig davon, ob sie sich bewegen oder nicht und deswegen ihr absoluter Bewegungszustand unbekannt bleiben müsse. Er präzisierte seine Uhrensynchronisationsmethode durch Licht und damit seine physikalische Interpretation der Ortszeit und erklärte, dass womöglich eine „neue Methode“ bzw. „neue Mechanik“ kommen werde, welche auf der Unüberschreitbarkeit der Lichtgeschwindigkeit (auch für relativ zum Äther bewegte Beobachter) beruhe. Er vermerkte jedoch kritisch an, dass sowohl das Relativitätsprinzip, Newtons actio und reactio, der Massenerhaltungssatz als auch der Energieerhaltungssatz keineswegs gesichert seien.[51]

Im November (1904) erkannte Cohn einige wichtige physikalische Interpretationen der lorentzschen Theorie (welche er mit seiner eigenen verglich) und verwies auf den engen Zusammenhang mit der Messung durch Maßstäbe und Uhren. Ruhen diese im lorentzschen Äther, zeigen sie die „wahren“ Längen und Zeiten an, und sind sie bewegt, zeigen sie kontrahierte bzw. dilatierte Werte an. Wie Poincaré machte Cohn die wichtige Feststellung, dass die Ortszeit dann zustande kommt, wenn Licht sich auf der Erde als Kugelwelle ausbreitet, d. h. die Lichtausbreitung auf der Erde als isotrop angenommen wird. Im Gegensatz zu Lorentz und Poincaré stellte Cohn nun fest, dass die Unterscheidung zwischen „wahren“ und „scheinbaren“ Koordinaten in der lorentzschen Theorie sehr künstlich anmutet, da kein Experiment den wahren Bewegungszustand aufzeigen kann und alle Koordinaten gleichberechtigt sind. Dagegen glaubte Cohn, dass dies alles nur für den Bereich der Optik gültig sei, wohingegen mechanische Uhren die „wahre“ Zeit anzeigen könnten.[52]

Friedrich Hasenöhrl (1904) verband Energie mit Trägheit in einer Schrift, welche nach seinen eigenen Worten sehr ähnlich zu denen von Abraham war. Hasenöhrl nahm an, dass ein Teil der Masse eines Körpers (die „scheinbare Masse“) als Strahlung in einem Hohlkörper aufgefasst werden kann. Die Trägheit dieser Strahlung ist proportional zu ihrer Energie nach der Formel m = (8 / 3)E / c2. Er bemerkte dazu den engen Zusammenhang von mechanischer Arbeit, Temperatur und scheinbarer Masse, da bei jeder Erwärmung Strahlung und somit zusätzliche Trägheit entsteht. Jedoch schränkte Hasenöhrl diese Energie-Scheinbare-Masse-Beziehung auf strahlende Körper ein; das hieß für Hasenöhrl, wenn ein Körper eine Temperatur hat, die größer ist als 0 Kelvin. Jedoch veröffentlichte er (1905) die Zusammenfassung eines Briefes, den Abraham an ihn geschrieben hatte, in welchem Abraham das Ergebnis bemängelte und als korrigierten Wert für die scheinbare Masse m = (4 / 3)E / c2 angab, also den gleichen Wert wie für die bereits bekannte elektromagnetische Masse. Hasenöhrl überprüfte seine eigenen Berechnungen und bestätigte Abrahams Resultat.[53]

Poincarés Dynamik des Elektrons

Am 5. Juni 1905 legte Poincaré schließlich die Zusammenfassung einer Arbeit vor, welche formal die vorhandenen Lücken von Lorentz’ Arbeit schloss. Diese Schrift enthielt zwar viele Ergebnisse, jedoch nicht die Herleitungen seiner Betrachtungen, wobei wesentliche Teile[54] davon bereits in zwei Briefen enthalten waren, welche von Poincaré ca. Mai 1905 an Lorentz geschrieben wurden.[55][56]. Er sprach vom Postulat der völligen Unmöglichkeit der Entdeckung einer absoluten Bewegung, welches scheinbar ein Naturgesetz sei. Er erkannte den Gruppencharakter der von ihm als Ersten so bezeichneten Lorentz-Transformation, er gab ihr die moderne symmetrische Gestalt und unter Benutzung der relativistischen Geschwindigkeitsaddition korrigierte er Lorentz’ Terme für Ladungsdichte und Geschwindigkeit und erreichte damit die volle Lorentz-Kovarianz. Lorentz folgend erklärte er, dass die Lorentz-Transformation (und damit die Lorentz-Invarianz) auf alle Kräfte der Natur angewendet werden müsse. Aber im Gegensatz zu Lorentz behandelte er auch die Gravitation und behauptete die Möglichkeit eines Lorentz-invarianten Gravitationsmodells und erwähnte die Existenz von Gravitationswellen. Um die Kritik von Abraham zu entkräften, führte Poincaré einen nicht-elektrischen Druck ein (die „Poincaré-Spannungen“), welcher die Stabilität des Elektrons garantieren soll und womöglich auch die Längenkontraktion dynamisch begründen sollte. Damit gab Poincaré jedoch das elektromagnetische Weltbild zugunsten des Relativitätsprinzips auf.[57][58]

Schließlich übermittelte Poincaré (vorgelegt am 23. Juli, gedruckt am 14. Dezember, veröffentlicht im Januar 1906) unabhängig von Einstein seine als Palermo-Arbeit bekannt gewordene Schrift, welche eine deutlich erweiterte Fassung von Poincarés erster 1905-Arbeit darstellte. Er sprach von dem „Postulat der Relativität“; er zeigte, dass die Transformationen eine Konsequenz des Prinzips der kleinsten Wirkung sind, und er demonstrierte ausführlicher als vorher deren Gruppeneigenschaft, wobei er den Namen Lorentz-Gruppe („Le groupe de Lorentz“) prägte. Er behandelte detailliert die Eigenschaften der Poincaré-Spannungen. Im Zusammenhang mit seiner Gravitationsauffassung (welche sich allerdings als unzureichend erwies) zeigte Poincaré, dass die Kombination x2 + y2 + z2 − c2t2 invariant ist und führte dabei den Ausdruck ict (im Gegensatz zu Palágyi also mit Lichtgeschwindigkeit) als vierte Koordinate eines vierdimensionalen Raums ein – er benutzte dabei eine Art von Vierervektor. Allerdings merkte Poincaré 1907 an, dass eine Neuformulierung der Physik in eine vierdimensionale Sprache zwar möglich, aber zu umständlich ist und deshalb geringen Nutzen habe, weshalb er seine diesbezüglichen Ansätze nicht weiterverfolgte – dies wurde später erst durch Minkowski getan. Und im Gegensatz zu Einstein hielt Poincaré weiterhin am Konzept des Äthers fest.[59][60]

Spezielle Relativitätstheorie

Albert Einstein (Fotografie aus dem Jahr 1921)

Einstein 1905

Spezielle Relativitätstheorie

In seiner Arbeit Zur Elektrodynamik bewegter Körper (übermittelt am 30. Juni, veröffentlicht im September 1905) gelang es Albert Einstein mit der speziellen Relativitätstheorie nicht nur, die maßgeblichen Teile der lorentzschen Elektrodynamik abzuleiten – die Theorie enthielt auch die „Abschaffung des Äthers“ und die Änderung der Grundlagen von Raum und Zeit. Dies beruhte alleine auf der Annahme von zwei Prinzipien, nämlich dem Relativitätsprinzip und der Konstanz der Lichtgeschwindigkeit in allen gleichförmig bewegten Bezugssystemen, wodurch sich der Übergang von der Galilei-Invarianz zu Lorentz-Invarianz sehr viel einfacher ergab. Vor allem Poincaré und nach 1905 auch Lorentz benutzten zum Teil dieselben Prinzipien wie Einstein, sie lehrten auch die vollständige mathematische Gleichberechtigung der Bezugssysteme und erkannten an, dass tatsächlich unterschiedliche Raum- und Zeitkoordinaten gemessen werden. Sie blieben aber dabei, die Effekte der Lorentz-Transformation auf dynamische Wechselwirkungen mit dem Äther zurückzuführen, unterschieden zwischen der „wahren“ Zeit im ruhenden Äthersystem und der „scheinbaren“ Zeit in relativ dazu bewegten Systemen und erwähnten den Äther bis zuletzt in ihren Schriften. Konkret bedeutet das, dass sie die newtonsche Mechanik zwar modifizieren, jedoch nicht grundlegend verändern wollten. Die grundlegende Neubewertung von Raum und Zeit im Rahmen einer wissenschaftlichen Theorie blieb also Einstein vorbehalten.[61][62]

Auf wenigen Seiten konnte Einstein aufgrund seiner axiomatischen Methode Ergebnisse herleiten, auf die andere vor ihm erst in jahrelanger, komplizierter Arbeit gestoßen waren. Einstein erklärte, dass der scheinbare Widerspruch zwischen den beiden Prinzipien (welche er als Postulate seiner Theorie zugrundelegte) durch die Untersuchung der Eigenschaften von Raum, Zeit und Gleichzeitigkeit aufgehoben werden konnte und die Einführung eines Äthers überflüssig wurde. Aus der Synchronisation von Uhren mit Lichtsignalen und der damit zusammenhängenden Relativität der Gleichzeitigkeit in den §§ 1–2 leitete er von rein kinematischen Überlegungen ausgehend im §3 die Lorentz-Transformation ab. Aus dieser Transformation konnte er wiederum als sekundäre Konsequenzen der Theorie die Längenkontraktion, die Zeitdilatation und das relativistische Geschwindigkeitsadditionstheorem in den §§ 4–5 ableiten. In den §§ 6–10 übertrug er nun die Ergebnisse seiner kinematischen Untersuchungen auf die Elektrodynamik. Er leitete den relativistischen Dopplereffekt und die relativistische Aberration aus den Transformationen ab, zeigte die Lorentz-Kovarianz der elektromagnetischen Gleichungen auf und berechnete die relativistischen Ausdrücke für den Strahlungsdruck. Schließlich leitete er die longitudinale und transversale Masse der Elektronen ab (letztere allerdings mit einem falschen Wert).

Äquivalenz von Masse und Energie

Bereits in der Arbeit zur Elektrodynamik gab Einstein die kinetische Energie eines Elektrons an mit:

E_\mathrm{kin} = mc^2 \left(\frac1{\sqrt{1-\frac{v^2} {c^2}}}-1\right)\,.

In seiner Arbeit „Ist die Trägheit eines Körpers von dessen Energieinhalt abhängig?“ vom September (veröffentlicht November) führte Einstein nun diesen Ansatz fort und erkannte, indem er ein ähnliches Strahlungsparadoxon im Sinne Poincarés (1900) auflöste, dass durch Übertragung von Energie ein Körper Masse verlieren und gewinnen kann, was zur eigentlichen Äquivalenz von Masse und Energie gemäß E = mc2 führt.[63] Wobei ähnliche Formeln zur „elektromagnetischen Masse“ wie oben erklärt schon von Thomson, Poincaré, Hasenöhrl usw. aufgestellt worden waren, jedoch wurde von diesen die Bedeutung der Formel nicht vollständig erkannt. Einstein hingegen konnte den tiefen Zusammenhang der Äquivalenz mit dem Relativitätsprinzip zeigen, und überdies war seine Herleitung völlig unabhängig von der Frage, ob die Masse elektromagnetischen Ursprungs ist oder nicht.

Frühe Rezeption

Erste Einschätzungen

Walter Kaufmann (1905, 1906) war wohl der Erste, der Bezug zur Arbeit Einsteins nahm. Er verglich die Theorien von Lorentz und Einstein, und obwohl er angab, dass die Methode Einsteins zu bevorzugen sei, stellte er die Beobachtungsäquivalenz der beiden Theorien fest. Deshalb sprach er vom Relativitätsprinzip als der „lorentz-einsteinschen“ Grundannahme. Dem folgend (1906a) veröffentlichte Max Planck seine erste Arbeit zu diesem Thema, wobei er darlegte, dass das Relativitätsprinzip durch Lorentz und in noch „allgemeinerer Fassung“ von Einstein eingeführt worden war. Dabei war Planck der Erste, der in einer weiteren Arbeit (1906b) für den Begriff „Lorentz-Einstein-Theorie“ den vom Relativitätsprinzip abgeleiteten Ausdruck „Relativtheorie“ einführte − im Gegensatz zur „Kugeltheorie“ von Abraham. In der darauf folgenden Diskussion zu der Arbeit wandelte Alfred Bucherer diesen Begriff in (Einsteinsche) „Relativitätstheorie“ ab. Viele (auch Einstein) benutzten auch häufig nur den Ausdruck „Relativitätsprinzip“ für die neue Methode. Alle diese Begriffe wurden in den nächsten Jahren abwechselnd von verschiedenen Physikern benutzt.[64]

Kaufmann-Bucherer-Experimente

Kaufmann (1905, 1906) gab nun die Ergebnisse seiner neu durchgeführten Experimente bekannt. Diese stellten seiner Meinung nach eine eindeutige Widerlegung des Relativitätsprinzips und der Lorentz-Einstein-Theorie dar, jedoch seien die Daten sehr gut verträglich mit der abrahamschen Theorie. Für einige Jahre stellten Kaufmanns Experimente einen gewichtigen Einwand gegen das Relativitätsprinzip dar.[65] Alfred Bucherer führte schließlich 1908 neue Experimente durch, welche die kaufmannschen Messungen überprüfen sollten. Diesmal jedoch wurde das Ergebnis von Bucherer als Bestätigung der „Lorentz-Einstein-Theorie“ und des Relativitätsprinzips interpretiert. Jedoch blieben auch hier Zweifel offen. Weitere Experimente von Neumann (1914) und anderen sprachen ebenfalls für die Relativitätstheorie, sodass man allgemein zur Überzeugung gelangte, dass die Sache entschieden sei. Jedoch spätere Untersuchungen zeigten, dass die Experimente von Kaufmann-Bucherer-Neumann im Grunde alle nicht genau genug waren, um eine Entscheidung zwischen den konkurrierenden Theorien herbeizuführen. Bei solchen Experimenten konnte erst 1940 die Lorentz-Einsteinsche Formel endgültig bestätigt werden.[66]

Relativistische Masse und Impuls

Max Planck

Planck (1906a) korrigierte den Fehler in Einsteins Definition der transversalen relativistischen Masse und zeigte, dass die korrekte Schreibweise mit der von Lorentz (1899) äquivalent war. Dabei definierte er auch den relativistischen Impuls.[67] Der Arbeit Plancks zum relativistischen Impuls folgend entwarfen Gilbert Newton Lewis (1908) und Richard C. Tolman (1912) das Konzept der relativistischen Masse, indem die Masse als Verhältnis von Impuls und Geschwindigkeit definiert wurde und nicht als Verhältnis von Kraft und Beschleunigung (zeitliche Impuls- bzw. Geschwindigkeitsänderung). Dadurch wurde die alte Definition für die longitudinale und transversale Masse überflüssig.[68]

Masse-Energie-Äquivalenz

Einstein (1906) stellte fest, dass die Trägheit der Energie (Masse-Energie-Äquivalenz) eine notwendige und hinreichende Bedingung für die Erhaltung der Schwerpunktsbewegung ist. Dabei verwies er auf Poincaré (1900b) und erklärte, dass der Inhalt dessen Arbeit hauptsächlich mit seiner eigenen übereinstimme.[69] Und Kurd von Mosengeil (1907) entwickelte Hasenöhrls Ansatz zur Berechnung der Schwarzkörperstrahlung in einem Hohlkörper unter Einbeziehung von Einsteins Theorie weiter und legte einen wichtigen Grundstein für die relativistische Thermodynamik – er erhielt dabei den gleichen Wert für die Masse der elektromagnetischen Strahlung wie Hasenöhrl. Auf Mosengeils Arbeit basierend konnte auch Planck (1907) die Masse-Energie-Äquivalenz aus dem Ansatz der Hohlraumstrahlung ableiten, und zusätzlich berücksichtigte er auch die Bindungskräfte in der Materie. Er anerkannte die Priorität von Einsteins 1905-Arbeit zur Äquivalenz, jedoch Planck schätzte seine eigene Ableitung als allgemeingültiger ein.[70]

Mitführungskoeffizient

Lorentz (1895) hatte bereits für Größen erster Ordnung den fresnelschen Mitführungskoeffizienten und somit das Fizeau-Experiment mit der Ortszeit erklären können. Analog dazu gelang es nun Jakob Laub und vollständig Max von Laue (1907), dieses Ergebnis für Größen aller Ordnungen aus dem relativistischen Geschwindigkeitsadditionstheorem abzuleiten.[71] Das Fizeau-Experiment stellt somit auch eine Bestätigung der Relativitätstheorie dar.

Weitere Arbeiten Einsteins

Einstein (1907) besprach die Frage, ob in starren Körpern, bzw. überhaupt, die Informationsgeschwindigkeit größer als Lichtgeschwindigkeit sein könne und erklärte, dass unter diesen Umständen Informationen in die Vergangenheit gesendet werden könnten und die Kausalität verletzt wäre. Da dies jedoch radikal gegen jede Erfahrung verstößt, ist Überlichtgeschwindigkeit ausgeschlossen. Er fügte hinzu, dass weitergehend eine Dynamik des starren Körpers in der SRT erstellt werden müsse (womit nun auch Einstein wie Planck und Bucherer den Ausdruck Relativitätstheorie benutzte). Einstein sagte auch zum ersten Mal die Nachprüfbarkeit des transversalen Dopplereffekts voraus. 1938 gelang es Herbert E. Ives und G. R. Stilwell tatsächlich, diesen Effekt und damit die Zeitdilatation experimentell nachzuweisen (Ives-Stilwell-Experiment).[72]

In einem bedeutenden Übersichtsartikel zum Relativitätsprinzip (1908a) bezeichnete Einstein den Inhalt der bisher erstellten Theorie als eine „Vereinigung der lorentzschen Theorie mit dem Relativitätsprinzip“ mit der Haupterkenntnis, dass die lorentzsche Ortszeit in Wirklichkeit eine reale, gleichberechtigte Zeit ist. Er präsentiert eine weitere Ableitung der Masse-Energie-Äquivalenz, wobei er in diesem Zusammenhang erstmals das Postulat aussprach, dass schwere und träge Massen äquivalent seien, und da die träge Masse vom Energiegehalt abhängt, gilt dies nach Einstein auch für die schwere Masse. Und schließlich folgerte er, dass bei Anwendung von SRT und Äquivalenzprinzip auf beschleunigte Systeme das Prinzip der Konstanz der Lichtgeschwindigkeit vollständig nur bei kleinen Lichtwegen zur Bestimmung der Gleichzeitigkeit benutzt werden kann, dass Lichtstrahlen in einem Gravitationsfeld gekrümmt sind und dass Uhren in einem höheren Gravitationspotential schneller gehen.

Emissionstheorie

Als eine Alternative zur Relativitätstheorie entwarfen Walter Ritz (1908) und andere eine an der newtonschen Korpuskulartheorie angelehnte Emissionstheorie, wonach die Lichtgeschwindigkeit in allen Bezugssystemen lediglich konstant relativ zur Emissionsquelle (und nicht zu einem Äther) ist und wo statt der Lorentz-Transformation die Galilei-Transformation verwendet wird (das heißt in Systemen, wo sich die Quelle mit ± v bewegt, breitet sich das Licht nicht mit Geschwindigkeit c, sondern mit c ± v aus). Diese Theorie verstößt also gegen die Lichtkonstanz, genügt aber trotzdem dem Relativitätsprinzip und kann das Michelson-Morley-Experiment erklären. Auch Albert Einstein zog vor 1905 eine solche Hypothese kurz in Betracht,[73] was auch der Grund war, dass er in seinen späteren Schriften das Michelson-Morley-Experiment zwar immer als Bestätigung des Relativitätsprinzips, nicht aber als Bestätigung der Lichtkonstanz verwendete.[74] Jedoch würde eine Emissionstheorie eine völlige Reformulierung der Elektrodynamik erfordern, wogegen der große Erfolg der maxwellschen Theorie sprach. Und schließlich gilt die Emissionstheorie seit der Entdeckung des Sagnac-Effekts und den Versuchen von Willem de Sitter (1913) als widerlegt, da bei einer solchen Theorie die beobachteten Bahnen bei Doppelsternen den Keplergesetzen scheinbar widersprechen müssten, was jedoch nicht beobachtet wurde.[75] Auch neuere Versuche mit hochfrequentem Licht bestätigen dieses Ergebnis und auch Versuche in Teilchenbeschleunigern konnten keine Quellenabhängigkeit der Lichtgeschwindigkeit nachweisen.[76]

Relativität der Gleichzeitigkeit

Die ersten Herleitungen der Relativität der Gleichzeitigkeit durch Synchronisation mit Lichtsignalen von Poincaré und Einstein wurden nun ebenfalls vereinfacht.[77] Daniel Frost Comstock schlug 1910 vor, in der Mitte zwischen zwei bei A und B befindlichen Uhren einen Sender zu platzieren, welcher ein Signal an beide Uhren sendet, die wiederum bei Ankunft des Signals in Gang gesetzt werden. Im System, in dem A und B ruhen, beginnen die Uhren synchron zu laufen. Jedoch aus der Sicht eines Systems, in dem A und B sich mit v bewegen, wird zuerst Uhr B in Gang gesetzt und danach erst Uhr A – die Uhren sind also nicht synchron. Auch Einstein entwarf 1917 ein Modell mit einem allerdings bewegten Empfänger in der Mitte zwischen A und B. Auch ließ er das Signal nicht von der Mitte aus starten, sondern sandte umgekehrt zwei Signale von A nach B zum Empfänger. Aus der Sicht des Systems, in dem A und B ruhen, werden die Signale gleichzeitig abgesendet – hier kommt jedoch der Empfänger dem Signal von B entgegen und läuft dem Signal von A davon und somit kommen die Signale nicht gleichzeitig an. Aus der Sicht des Systems hingegen, in dem der Empfänger ruht, interpretiert man dieses ungleichzeitige Eintreffen damit, dass die Signale von vornherein nicht gleichzeitig von A und B gesendet wurden.

Physik der Raumzeit

Minkowskis Raumzeit

Hermann Minkowski

Poincarés vierdimensionaler Ansatz wurde von Hermann Minkowski (1907) entscheidend weiterentwickelt. Diese Geometrisierung der Lorentz-Transformation beruhte beispielsweise auf mathematischen Errungenschaften wie Gruppentheorie, Invariantentheorie und Projektive Geometrie, wie sie im 19. Jahrhundert von Mathematikern wie Arthur Cayley entwickelt wurden. In einem Vortrag von 1907 führte Minkowski nun die Raumzeit als eine „vierdimensionale nicht-Euklidische Mannigfaltigkeit“ ein. Es gelang ihm, die gesamte Elektrodynamik durch Einführung eines vierdimensionalen Formalismus im sogenannten Minkowski-Raum neu zu formulieren, was eine sehr viel klarere und zusammenhängendere Interpretation der SRT ermöglichte. Dabei führte er wichtige Begriffe wie Eigenzeit, Lorentz-Invarianz ein und verwendete Vierervektoren, welche er allerdings anders nannte. Jedoch sein Versuch ein Lorentz-invariantes Gravitationsgesetz aufzustellen, erwies sich als genauso untauglich wie das Modell von Poincaré. In seinem berühmten Vortrag Raum und Zeit (1908), wo er das Ende der bisherigen Vorstellungen von Raum und Zeit verkündete, konzipierte er das Minkowski-Diagramm zur Veranschaulichung der Raumzeit.

Minkowski selbst nannte 1907 als seine Vorläufer bei der Ausarbeitung des Relativitätsprinzips: Lorentz, Einstein, Poincaré und Planck. Hingegen in seinem berühmten Vortrag Raum und Zeit erwähnte er nur noch Voigt, Lorentz und Einstein. Dabei kritisierte er Lorentz für die Künstlichkeit seiner Kontraktionshypothese, wohingegen er seine eigene geometrische Deutung als viel natürlicher ansah. Einstein würdigte er vor allem für seine vollständige Relativierung der Zeit, jedoch bemängelte er, dass sowohl Lorentz als auch Einstein die Relativität des Raumes nicht vollständig berücksichtigt hätten. Minkowskis Prioritätsansprüche in Bezug zur Vervollständigung der Relativitätstheorie werden in diesem Zusammenhang von den Wissenschaftshistorikern jedoch zurückgewiesen. Dies deswegen, da Minkowski (wie Wien und Abraham) weiterhin ein Vertreter des elektromagnetischen Weltbildes blieb und offenbar nicht vollständig den Unterschied zwischen der lorentzschen Elektronentheorie und der einsteinschen Kinematik erkannt hatte.[78][79]

Vorerst lehnten Einstein und Laub jedoch eine vierdimensionale Formulierung der Relativitätstheorie als zu aufwendig ab und veröffentlichten eine nicht-vierdimensionale Ableitung der Grundgleichungen für bewegte Körper. Trotzdem war es gerade Minkowskis Formalismus, welcher ab 1909 entscheidend für die Verbreitung und Akzeptanz der SRT verantwortlich war.[80]

Vektor-Notation und geschlossene Systeme

Besonders bedeutend war nun die Tatsache, dass Minkowskis Konzept formal beträchtlich verfeinert und modernisiert wurde.[79] Beispielsweise ersetzte Arnold Sommerfeld (1910) Minkowskis Matrix-Notation mit einer eleganteren Vektor-Notation und gebrauchte dabei erstmals Begriffe wie „Vierervektor“ oder „Sechservektor“. Er führte auch eine trigonometrische Herleitung der Geschwindigkeitsaddition ein, welche seiner Ansicht nach viel von der Fremdartigkeit dieses Konzepts entfernte. Weitere wichtige Beiträge wurden von Laue erbracht.[81][82] Er erweiterte Minkowskis Ausdrücke auch auf nicht-elektromagnetische Prozesse und vertiefte so das Konzept der Masse-Energie-Äquivalenz. Laue zeigte auch, dass nicht-elektrische Kräfte benötigt werden, damit alle Kräfte im Elektron korrekt der Lorentz-Transformation unterworfen sind, und damit das Elektron stabil bleibt – das heißt, er zeigte, dass die Poincaré-Spannungen eine natürlich Konsequenz der SRT ist, damit das Elektron ein geschlossenes System bildet.

Reziprozität der Zeitdilatation und das Zwillingsparadoxon

Lewis und Tolman (1909) veranschaulichten die von Einstein geforderte Reziprozität der Zeitdilatation durch Benutzung zweier Lichtuhren A und B, welche sich mit einer bestimmten Relativgeschwindigkeit zueinander bewegen. Die Uhren bestehen aus zwei Spiegeln, zwischen welchen jeweils ein Lichtsignal hin- und hergeschickt wird. Für einen Beobachter, welcher im selben Inertialsystem wie A ruht, ist der Laufweg des Signals einfach der Abstand zwischen ihnen durch die Lichtgeschwindigkeit. Betrachten sie jedoch Uhr B, bemerken sie dass dort die Laufzeit länger ist, weil der Lichtstrahl sich geneigt ausbreiten muss, um sein Ziel zu erreichen – A geht also schneller als B. Hingegen ein bei B ruhender Beobachter sieht es genau umgekehrt: Hier ruht B, und A ist bewegt, und folglich ist B die schneller laufende Uhr. Und in einem Vortrag zwischen 1910 und 1912 diskutierte Lorentz ebenfalls Reziprozität der Zeitdilatation und damit zusammenhängend ein scheinbares Uhrenparadoxon. Lorentz zeigt, dass es sich bei der Aussage, dass jeder die Uhr des anderen jeweils langsamer wahrnimmt, nicht um ein Paradoxon handelt. Es muss nämlich bedacht werden, dass in einem System nur mit einer Uhr gemessen wird, im anderen jedoch zwei Uhren erforderlich sind – in diesem Fall muss auch die Relativität der Gleichzeitigkeit berücksichtigt werden.

Max von Laue

Weiters kreierte Paul Langevin (1911) mit dem berühmten Zwillingsparadoxon eine ähnliche Situation, indem er die Uhren mit Zwillingen ersetzte. Langevin löste das Paradoxon auf, indem er auf die Asymmetrie der beiden Beobachter hinwies, wonach ein Körper einen durch Beschleunigung verursachten Richtungswechsel vollführt. Langevin selbst sah das jedoch als Hinweis auf eine „absolute Bewegung“ in einem Äther. Obwohl diese Erklärung bis heute im Prinzip beibehalten wurde, werden seine Folgerungen in Bezug auf den Äther abgelehnt. Zum Beispiel wies Max von Laue (1913) darauf hin, dass die Beschleunigung in Bezug auf die inertiale Bewegung beliebig klein gemacht werden kann. Dadurch konnte Laue zeigen, dass es von weit wichtigerer Bedeutung ist, dass sich der reisende Zwilling während seiner Reise beim Hin- und Rückflug in zwei Inertialsystemen befindet, während der zurückgebliebene Zwilling in einem einzigen verbleibt. Laue war auch der Erste, der dies mit Minkowski-Diagrammen veranschaulichte und feststellte, wie die Weltlinien von inertial bewegten Beobachtern die Eigenzeit zwischen zwei Ereignissen maximieren.[83]

Starre Körper und Realität der Längenkontraktion

Paul Ehrenfest veröffentlichte 1909 das nach ihm benannte ehrenfestsche Paradoxon, wonach aufgrund der Lorentzkontraktion sich der Umfang einer rotierenden Scheibe bei gleich bleibendem Radius verkürzt. Dies stand im Zusammenhang mit der bereits von Einstein (1907) aufgeworfenen Frage, inwiefern der Begriff des starren Körpers in der SRT anwendbar sei, was 1909 unter anderem von Max Born, Gustav Herglotz, Fritz Noether, und 1911 von Max von Laue untersucht wurde. Dabei erkannte Laue, dass in der SRT ein Körper unendlich viele Freiheitsgrade besitzt, das heißt es gibt überhaupt keine „starren“ Körper.[84] Im Zusammenhang mit dem ehrenfestschen Paradoxon wurde von Vladimir Varičak (1911) die Frage diskutiert, ob die Längenkontraktion „real“ oder „scheinbar“ sei. Es handelte sich hierbei jedoch eher um einen Streit um Worte, denn wie Einstein in seiner Antwort an Varičak ausführte, ist die kinematische Längenkontraktion zwar insofern „scheinbar“, da sie für einen mitbewegten Beobachter nicht existiert, jedoch für einen nicht mitbewegten Beobachter ist sie sehr wohl „real“ und ihre Konsequenzen sind messbar.[85] Was die Messergebnisse betrifft, ergibt sich für die Kontraktionshypothese von Lorentz das Gleiche: Auch hier ist die Kontraktion nur für einen nicht mitbewegten Beobachter messbar, nicht jedoch für einen mitbewegten. Der fundamentale Unterschied liegt in der Interpretation − während nach Einstein die Kontraktion eine Folge von kinematischen Effekten wie der (un-)gleichzeitigen Messung der Endpunkte einer Strecke ist, handelt es sich bei Lorentz um einen dynamisch-mechanischen, durch im Äther übermittelte Kräfte verursachten Effekt.

Lorentz-Transformation ohne Lichtpostulat

Es wurden nun auch Versuche gemacht, die Lorentz-Transformation ohne Einbeziehung des Postulats der Konstanz der Lichtgeschwindigkeit herzuleiten. Wladimir Sergejewitsch Ignatowski (1910) z. B. benutzte zu diesem Zweck a) das Relativitätsprinzip, b) Isotropie und Homogenität und Raumes, c) die Forderung der Reziprozität. Philipp Frank und Hermann Rothe (1910) zeigten nun auf, dass diese Herleitung unvollständig ist und auf anderen Zusatzannahmen beruhte, welche von Ignatowski nicht aufgeführt wurden. Ihre eigene Herleitung beruhte auf den Annahmen, dass a) die Lorentz-Transformation eine einparametrige, homogene lineare Gruppe bilden soll, b) dass bei Wechsel des Bezugssystems die Relativgeschwindigkeit nur das Vorzeichen wechselt, c) dass die Längenkontraktion ausschließlich von der Relativgeschwindigkeit abhängt. Nach Pauli und Miller waren jedoch sowohl Ignatowski als auch Frank/Rothe nicht in der Lage, in den erhaltenen Transformationen die invariante Geschwindigkeit mit der Lichtgeschwindigkeit zu identifizieren, da beispielsweise Ignatowski auf die Elektrodynamik zurückgreifen musste, um die Lichtgeschwindigkeit zu erhalten. Pauli vertrat daher die Meinung, dass beide Postulate für die Herleitung der Lorentz-Transformation notwendig sind.[86][87] Jedoch wird bis heute versucht, die Transformationen ohne Benutzung des Lichtpostulats abzuleiten.

Nichteuklidische Reformulierungen der Theorie

Obwohl Minkowski bereits 1907 feststellte, dass der Raumzeit-Formalismus einen engen Zusammenhang zur nichteuklidischen Geometrie besitzt, verfolgte er diesen Gedanken nicht weiter.[88] Auch aus der Arbeit von Born (1909) über die starren Körper wurden Analogien zur riemannschen Geometrie deutlich,[89] wobei damit zusammenhängend das ehrenfestsche Paradoxon für Einstein ein wichtiger Fingerzeig bei seiner zu entwickelnden Gravitationstheorie war. Systematische Versuche, die gesamte SRT auf Basis einer nichteuklidischen Geometrie zu reformulieren, wurden jedoch erst von Physikern wie Alfred Robb (1911) gemacht, der beispielsweise den Begriff der Rapidität als Hyperbelfunktion zur Beschreibung der Systemgeschwindigkeit einführte. Vladimir Varičak (1912) bemerkte die Analogie zur hyperbolischen Geometrie und versuchte damit die SRT neu zu formulieren. Jedoch erbrachten seine Beiträge keine neuen physikalischen Einsichten. Edwin Bidwell Wilson und Gilbert Newton Lewis (1912) führten eine nichteuklidische Vektorrechnung ein, welche jedoch nicht akzeptiert und von ihnen auch nicht weiterverfolgt wurde. Eine wichtige Entdeckung machte Émile Borel (1913), welcher auf Basis einer hyperbolischen Geometrie die kinematische Grundlage der Thomas-Präzession legte. Jedoch wurde Minkowskis ursprünglicher Raumzeit-Formalismus weiterhin bevorzugt[88] und es dauerte bis zur Entwicklung der allgemeinen Relativitätstheorie, bis die nichteuklidischen Geometrie eine wichtige Rolle in der Physik spielte.

Akzeptanz der Theorie

Es kristallisierte sich nun endgültig der wesentliche interpretatorische und philosophische Unterschied zwischen den Theorien von Lorentz und Einstein heraus. Es wurde nicht mehr der Begriff „Lorentz-Einstein-Theorie“ benutzt und kaum noch jemand (mit Ausnahmen wie Lorentz, Poincaré und Langevin) bekannte sich noch zur Existenz eines Äthers in irgendeiner Form. So verglich Planck bereits 1909 die Auswirkungen des modernen Relativitätsprinzips − mit Blick auf Einsteins vollständige Relativierung der Zeit − mit den Umwälzungen durch das kopernikanische Weltsystem.[90] Besonders bedeutend war auch die Tatsache, dass das Raumzeit-Konzept Minkowskis formal beträchtlich verfeinert und modernisiert wurde, was um 1913 der SRT insbesondere unter Mathematikern und theoretischen Physikern zum Durchbruch verhalf.[91] Einstein selbst war zu dieser Zeit schon intensiv mit der Ausarbeitung der allgemeinen Relativitätstheorie beschäftigt, wobei er 1915 schließlich zur Unterscheidung der Theorien erstmals den Ausdruck „Spezielle Relativitätstheorie“ gebrauchte.

Zusammenfassung und Rückblick

Obwohl hier die geschichtliche Entwicklung im Vordergrund steht, ist rückblickend eine kurze Zusammenfassung aus größerem Abstand sinnvoll, zumal die Entwicklung sehr kompliziert verlaufen ist. Zunächst bestand ein Dilemma darin, dass zwar die Gleichungen der newtonschen Mechanik, nicht aber die der maxwellschen Elektrodynamik, die Eigenschaft der Invarianz gegen Galilei-Transformationen besitzen. Diesem Dilemma entsprach die Vorstellung eines speziellen Mediums, des Äthers, für die Phänomene der letztgenannten Theorie.

Nach wesentlichen Vorarbeiten von Lorentz und Poincaré stellte Einstein in der speziellen Relativitätstheorie fest

  • dass die Galilei-Transformationen durch die Lorentz-Transformationen zu ersetzen sind,
  • dass also die newtonsche Mechanik modifiziert werden muss, nicht aber die maxwellsche Elektrodynamik, die ja schon Lorentz-invariant ist,
  • dass hernach, also mit den lorentzschen Transformationen anstelle der von Galilei, relativistische Invarianz für alle physikalischen Phänomene bestehe,
  • dass der „Äther“ vollständig abzuschaffen sei,
  • und dass stattdessen die Vorstellungen von Raum und Zeit radikal zu ändern seien, und zwar entsprechend den Lorentz-Transformationen.

Bezüglich der Abschaffung des Äthers und der Einführung neuer Vorstellungen zu Raum und Zeit waren Poincaré und Lorentz anderer Meinung als Einstein. Rückblickend kann man also sagen, dass Einstein „revolutionär“, Poincaré und Lorentz dagegen „konservativ“ eingestellt waren. Letztlich hat sich Einstein durchgesetzt.

Kritik

Einige wie Max Abraham, Friedrich Adler, Henri Bergson, Herbert Dingle, Hugo Dingler, Louis Essen, Salomo Friedlaender, Herbert E. Ives, Oskar Kraus, Emanuel Lasker, Hjalmar Mellin, Albert Abraham Michelson, Menyhért Palágyi, Walter Ritz und Georges Sagnac lehnten die SRT ab. Gründe dafür waren beispielsweise eigene physikalische Theorien, philosophische Einwände, Ablehnung der abstrakt-mathematischen Methode, Unverständnis, und angebliche Fehler in der Theorie. Dazu kamen noch Philipp Lenard, Johannes Stark, Ernst Gehrcke, Paul Weyland, Bruno Thüring im Rahmen der Deutschen Physik, wo neben den genannten Gründen auch Antisemitismus eine Rolle spielte. Heute spielen diese Kritiken in der Fachwelt praktisch keine Rolle mehr, da die SRT als widerspruchsfrei eingestuft wird und eine große Anzahl experimenteller Bestätigungen vorliegen.

Für nähere Details siehe den Artikel → Kritik an der Relativitätstheorie.

Priorität

Edmund Taylor Whittaker sprach 1953 in der zweiten Ausgabe seiner bekannten History of the theories of aether and electricity von der Relativitätstheorie als der Schöpfung von Poincaré und Lorentz und maß Einsteins Beiträgen nur sekundäre Bedeutung bei.[92] Dies ist jedoch nicht die Meinung der überwiegenden Mehrheit der Fachwelt. Wissenschaftshistoriker wie Gerald Holton,[93] Arthur I. Miller,[94] Abraham Pais,[95] und John Stachel erkennen die Leistungen Poincarés an, jedoch wird betont, dass Einstein als Erster die vollständige Relativierung von Raum und Zeit an sich lehrte, den (klassischen) Äther aus der Physik verbannte, und erst damit den Weg in eine grundlegend neue Theorie geebnet hat. Andere Wissenschaftshistoriker gehen etwas weiter und bezeichnen Poincarés Theorie als eine Art „relativistische Physik“ (Katzir)[96] bzw. „Relativitätstheorie“ (Walter)[97] − wenn auch nicht dieselbe wie Einsteins SRT. Hingegen wird die Meinung, dass Poincaré (und Lorentz), und nicht Einstein, die wahren Begründer der heute gelehrten SRT seien, nur noch außerhalb des wissenschaftlichen Mainstreams vertreten (z. B. Logunov).[98]

Lorentz

Obwohl Lorentz weiterhin am Äthergedanken festhielt, sprach er in seinem Hauptwerk The theory of electrons (1909) voll Anerkennung über „Einsteins Relativitätsprinzip“ und seinen Ausführungen über Uhren, Maßstäbe, und Synchronisation. Einsteins große Leistung sei es gewesen, durch die völlige Gleichsetzung der unterschiedlichen Inertialsysteme (insbesondere der Zeitvariable), Lorentz’ umständliche Formulierung durch eine sehr viel durchsichtigere und einfachere zu ersetzen. Bemerkenswert ist, dass weder hier noch in der Neuausgabe (1916) der Name von Poincaré in diesem Zusammenhang erwähnt wird.[99]

Hingegen würdigte Lorentz in einer 1914 geschriebenen, aber erst 1921 veröffentlichten Arbeit vor allem Poincaré für seine Arbeiten von 1905/1906. Er verwies auf diesen als den ersten, der die formale Gleichwertigkeit der Ortszeit mit der „normalen“ Zeit erkannte, während er selbst sie als mathematischen Trick angesehen hatte. Deswegen habe er selbst nicht die korrekte Anwendung der Transformation angeben können – dies wurde zuerst von Poincaré und später von Einstein und Minkowski getan. Auch habe Poincaré vor ihm die grundlegende Bedeutung des Relativitätsprinzips für die Elektrodynamik erkannt und als erster den Begriff „Postulat“ dafür verwendet. Zuletzt wies er auf die (im Abschnitt „Lorentz-Transformation“ dargestellten) von Poincaré gemachten grundlegenden Erkenntnisse hin.[100]

Abgesehen von dieser Ausnahme erwähnte Lorentz jedoch weiterhin nur Einstein in diesem Zusammenhang. Beispielsweise deutete Michelson 1927 an, dass Lorentz der Urheber der Relativitätstheorie sei. Lorentz antwortete, dass er zu der Zeit, als Einstein seine Theorie erstellte, seine Zeittransformation nur als heuristische Arbeitshypothese betrachtete. Die Relativitätstheorie sei auch wirklich allein Einsteins Werk – es könne keinen Zweifel geben, dass Einstein sie entdeckt hätte, selbst wenn die Arbeit seiner Vorgänger auf diesem Gebiet überhaupt nicht gemacht worden wäre.

Poincaré

Poincaré hingegen stellte die neuen Theorien immer als Schöpfung von Lorentz dar und sah keinen Grund, Einstein und Minkowski im Zusammenhang mit diesen Theorien überhaupt zu erwähnen.[101] So schreibt er noch 1912 kurz vor seinem Tod zu der Frage, ob die „lorentzsche Mechanik“ auch nach der Entwicklung der Quantentheorie Bestand haben wird:

„In allen den Punkten, in denen die lorentzsche Mechanik von der newtonschen abweicht, bleibt sie zu Recht bestehen. Man glaubt nach wie vor, dass ein beweglicher Körper unter keinen Umständen jemals eine größere Geschwindigkeit als die des Lichtes annehmen kann, dass die Masse eines Körpers keine unveränderliche Größe ist, sondern von seiner Geschwindigkeit abhängt und von dem Winkel, den diese Geschwindigkeit mit der auf den Körper wirkenden Kraft einschließt, ferner, dass kein Versuch jemals wird entscheiden können, ob ein Körper, absolut genommen, sich im Zustande der Ruhe oder in dem der Bewegung befinde, sei es nun in Bezug auf den Raum als solchen, sei es selbst in Bezug auf den Äther.“

Einstein

Einsteins Arbeit zur Elektrodynamik (1905) enthält keine Referenzen zu anderen Werken. Deshalb verweisen die Einstein-Biographen Abraham Pais und Albrecht Fölsing im Zusammenhang mit dessen Literaturrezeption auf folgendes Einstein-Zitat von 1907:[22][102]

„Es scheint mir in der Natur der Sache zu liegen, daß das Nachfolgende zum Teil bereits von anderen Autoren klargestellt sein dürfte. Mit Rücksicht darauf jedoch, daß hier die betreffenden Fragen von einem neuen Gesichtspunkt aus behandelt sind, glaubte ich, von einer für mich sehr umständlichen Durchmusterung der Literatur absehen zu dürfen, zumal zu hoffen ist, daß diese Lücke von anderen Autoren noch ausgefüllt werden wird, wie dies in dankenswerter Weise bei meiner ersten Arbeit über das Relativitätsprinzip durch Hrn. Planck und Hrn. Kaufmann bereits geschehen ist.“

In einem Brief an Stark von 1907 schrieb Einstein darüber hinaus, dass er aufgrund seiner Tätigkeit in Patentamt kaum Gelegenheit habe, einschlägige Fachliteratur in den Bibliotheken zu studieren. Das heißt allerdings nicht, dass Einstein generell nicht über den Stand der Wissenschaft orientiert gewesen war, sondern er dürfte auf bestimmten Bereichen durchaus gut informiert gewesen sein.[103][102] Und so versuchen einige Wissenschaftshistoriker, die von Einstein benutzte Quellen aufzulisten.

In philosophischer Hinsicht gab Einstein an, von den empiristischen Philosophen David Hume und Ernst Mach beeinflusst worden zu sein. Möglicherweise hatte Einstein auch Kenntnis der wichtigen Arbeiten von Wien, Cohn, Abraham, Bucherer, oder Hasenöhrl in den Annalen der Physik, da er selbst ab 1901 mehrere Artikel in diesem Journal veröffentlichte. So verwendete er Abraham folgend den Ausdruck „Maxwell-Hertzsche Gleichungen“ und „in Anlehnung an die übliche Betrachtungsweise“ die Begriffe der transversalen und longitudinalen Masse. Schließlich erwähnt er in § 9 die „lorentzsche Theorie der Elektrodynamik“.[103] Weiters veröffentlichte Einstein in Beiblätter zu den Annalen der Physik allein im Jahr 1905 einundzwanzig Reviews über vor allem thermodynamische Arbeiten.[104] Jürgen Renn, Direktor vom Max-Planck-Institut für Wissenschaftsgeschichte, schrieb:[105]

„The Annalen also served as a source of modest additional income for Einstein, who wrote more than twenty reports for its Beiblätter - mainly on the theory of heat - thus demonstrating an impressive mastery of the contemporary literature. This activity started in 1905 and probably resulted from his earlier publications in the Annalen in this field. Going by his publications between 1900 and early 1905, one would conclude that Einstein's specialty was thermodynamics.“

Deutsche Übersetzung:

„Die Annalen dienten ebenso als eine Quelle für ein bescheidenes, zusätzliches Einkommen für Einstein, der mehr als zwanzig Berichte für ihre Beiblätter schrieb – hauptsächlich über die Theorie der Wärme – und so eine eindrucksvolle Beherrschung der zeitgenössischen Literatur demonstrierte. Diese Aktivität begann 1905 und resultierte wahrscheinlich aus seinen früheren Publikationen in den Annalen auf diesem Gebiet. Von seinen Publikationen zwischen 1900 und Anfang 1905 ausgehend, könnte man schließen dass Einsteins Spezialgebiet die Thermodynamik war.“

Eine wichtige Quelle war auch August Föppls Lehrbuch zur Elektrodynamik (1894), welches Maxwells Theorie in der Formulierung von Heaviside und Hertz und eine Variante des für Einstein im Zusammenhang mit dem Relativitätsprinzip wichtigen „Bewegter-Magnet-und-Leiter“ Problems enthielt.[106][103] Dazu kam noch Einsteins Tätigkeit als Patentprüfer, wo er möglicherweise mit diversen Patenten zur Uhrensynchronisation auf elektrischer Basis zu tun hatte.[107] Auch kannte er die Arbeit von Lorentz von 1895, wo dieser die Ortszeit, die Längenkontraktion, und das Michelson-Morley-Experiment beschrieb.[108] Wie er 1909 ausführte, entnahm Einstein das Prinzip der Lichtkonstanz deswegen auch dem lorentzschen Äther (bzw. den „Maxwell-Lorentzschen“ Gleichungen). Einstein kam dabei zur Überzeugung, dass die Ortszeit eine reale, gleichberechtigte Zeitangabe sei, und nicht nur ein mathematischer Trick. Und er erkannte im Gegensatz zu Poincaré und Lorentz, dass gerade die Gleichberechtigung der Bezugssysteme und damit die Unentdeckbarkeit des Äthers den Ätherbegriff überhaupt sinnlos machte.[73] 1912 fasste er dies so zusammen:

„Es ist allgemein bekannt, dass auf das Relativitätsprinzip allein eine Theorie der Transformationsgesetze von Raum und Zeit nicht gegründet werden kann. Es hängt dies bekanntlich mit der Relativität der Begriffe "Gleichzeitigkeit" und "Gestalt bewegter Körper" zusammen. Um diese Lücke auszufüllen, führte ich das der H.A. Lorentzschen Theorie des ruhenden Lichtäthers entlehnte Prinzip der Konstanz der Lichtgeschwindigkeit ein, das ebenso wie das Relativitätsprinzip eine physikalische Voraussetzung enthält, die nur durch die einschlägigen Erfahrungen gerechtfertigt erschien (Versuche von Fizeau, Rowland usw.).“

Es ist auch bekannt, dass er vor 1905 mit Maurice Solovine und Conrad Habicht in der Akademie Olympia Poincarés Buch Wissenschaft und Hypothese, welches sie „Wochen hindurch fesselte und faszinierte“, gelesen hat.[109][110] Ob Einstein eine der anderen Arbeiten Poincarés vor 1905 gelesen hat, bleibt unklar. In seinen wissenschaftlichen Schriften nach 1905 bezieht sich Einstein auf Poincaré nur im Zusammenhang mit der Trägheit der Energie (1906) und der nichteuklidischen Geometrie (1921), nicht jedoch auf dessen Leistungen bei der Formulierung der Lorentztransformation, dem Zusammenhang zwischen Uhrensynchronisation und Gleichzeitigkeit, oder des Relativitätsprinzips. Erst 1953, anlässlich des 50-jährigen Bestehens der SRT, erwähnte er erstmals Poincaré − vielleicht deswegen, weil Abraham Pais um 1950 Einstein eine Kopie von Poincarés Palermo-Arbeit überlassen hatte. Er schrieb:[111]

„Hoffentlich wird dafür gesorgt daß die Verdienste von H.A. Lorentz und H. Poincaré bei dieser Gelegenheit ebenfalls sachgemäß gewürdigt werden.“

Und 1955 schrieb er an Carl Seelig (wobei allerdings auch Poincaré bereits die Lorentz-Invarianz als Grundbedingung für alle Theorien betont hatte):[108]

„Es ist zweifellos, dass die spezielle Relativitätstheorie, wenn wir ihre Entwicklung rückschauend betrachten, im Jahre 1905 reif zur Entdeckung war. Lorentz hatte schon erkannt, dass für die Analyse der maxwellschen Gleichungen die später nach ihm benannte Transformation wesentlich sei, und Poincaré hat diese Erkenntnis noch vertieft. Was mich betrifft, so kannte ich nur Lorentz bedeutendes Werk von 1895 "La theorie electromagnetique de Maxwell" und "Versuch einer Theorie der elektrischen und optischen Erscheinungen bewegten Körpern", aber nicht Lorentz' spätere Arbeiten, und auch nicht die daran anschließende Untersuchung von Poincaré. In diesem Sinne war meine Arbeit von 1905 selbständig. [..] Was dabei neu war, war die Erkenntnis, dass die Bedeutung der Lorentztransformation über den Zusammenhang mit den maxwellschen Gleichungen hinausging und das Wesen von Raum und Zeit im allgemeinen betraf. Auch war die Einsicht neu, dass die "Lorentz-Invarianz" eine allgemeine Bedingung sei für jede physikalische Theorie. Das war für mich von besonderer Wichtigkeit, weil ich schon fruher erkannt hatte, daß die Maxwellsche Theorie die Mikrostruktur der Strahlung nicht darstelle und deshalb nicht allgemein haltbar sei.“

Literatur

Primärquellen

  • Abraham, Max: Dynamik des Elektrons. In: Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen, Mathematisch-Physikalische Klasse. 1902, S. 20–41
  • Bucherer, Alfred: Messungen an Becquerelstrahlen. Die experimentelle Bestätigung der Lorentz-Einsteinschen Theorie.. In: Physikalische Zeitschrift. 9, Nr. 22, 1908, S. 755–762
  • Bucherer, A. H.: Die experimentelle Bestätigung des Relativitätsprinzips. In: Annalen der Physik. 333, Nr. 3, 1909, S. 513–536. doi:10.1002/andp.19093330305
  • Cohn, Emil: Zur Elektrodynamik bewegter Systeme. In: Sitzungsberichte der Königlich Preußische Akademie der Wissenschaften. 40, 1904, S. 1294–1303, 1404-1416
  • Comstock, Daniel Frost: The principle of relativity. In: Science. 31, 1910, S. 767-772
  • Ehrenfest, Paul: Gleichförmige Rotation starrer Körper und Relativitätstheorie. In: Physikalische Zeitschrift. 10, 1909, S. 918
  • Einstein Albert: Über die spezielle und die allgemeine Relativitätstheorie, §8-9. Berlin-Heidelberg-New York: Springer 1917, ISBN 3-540-42542-0 Siehe auch englischer Volltext
  • FitzGerald, George Francis: The Ether and the Earth’s Atmosphere. In: Science. 13, 1889, S. 390
  • Oliver Heaviside: Electromagnetic waves, the propagation of potential, and the electromagnetic effects of a moving charge. In: Electrical papers, 2, S. 490–499 1888/1894
  • Oliver Heaviside: On the Electromagnetic Effects due to the Motion of Electrification through a Dielectric. In: Philosophical Magazine. 27, Nr. 167, 1889, S. 324–339
  • Ignatowsky, W. v.: Einige allgemeine Bemerkungen über das Relativitätsprinzip. In: Physikalische Zeitschrift. 11, 1910, S. 972–976
  • Kaufmann, Walter: Über die Konstitution des Elektrons. In: Sitzungsberichte der Königlich Preußische Akademie der Wissenschaften. 45, 1905, S. 949–956
  • Laue, Max von: Zur Diskussion über den starren Körper in der Relativitätstheorie. In: Physikalische Zeitschrift. 12, 1911b, S. 85–87
  • Laue, Max von: Das Relativitätsprinzip, 2, Braunschweig: Vieweg 1913
  • Lewis, Gilbert N.: A revision of the Fundamental Laws of Matter and Energy. In: Philosophical Magazine. 16, 1908, S. 705–717
  • Lewis, Gilbert N. & Tolman, Richard C.: The Principle of Relativity, and Non-Newtonian Mechanics. In: Proceedings of the American Academy of Arts and Sciences. 44, 1909, S. 709–726
  • Lorentz, Hendrik Antoon: De l’influence du mouvement de la terre sur les phénomènes lumineux. In: Archives néerlandaises des sciences exactes et naturelles. 21, 1886, S. 103–176
  • Lorentz, Hendrik Antoon: Die relative Bewegung der Erde und des Äthers. In: Abhandlungen über Theoretische Physik, S. 443–447, Leipzig: B.G. Teubner 1892b/1907
  • Lorentz, Hendrik Antoon: Versuch einer Theorie der electrischen und optischen Erscheinungen in bewegten Körpern. Leiden: E.J. Brill 1895
  • Lorentz, Hendrik Antoon: Simplified Theory of Electrical and Optical Phenomena in Moving Systems. In: Proceedings of the Royal Netherlands Academy of Arts and Sciences. 1, 1899, S. 427–442
  • Lorentz, Hendrik Antoon: Considerations on Gravitation. In: Proceedings of the Royal Netherlands Academy of Arts and Sciences. 2, 1900, S. 559–574
  • Lorentz, Hendrik Antoon: Electromagnetic phenomena in a system moving with any velocity smaller than that of light. In: Proceedings of the Royal Netherlands Academy of Arts and Sciences. 6, 1904b, S. 809–831
  • Lorentz, Hendrik Antoon: Lectures on theoretical physics, 3. London: MacMillan 1910/1931
  • Lorentz, Hendrik Antoon & Einstein, Albert & Minkowski, Hermann: Das Relativitätsprinzip. Leipzig & Berlin: B.G. Teubner 1913
  • Lorentz, Hendrik Antoon: La Gravitation. In: Scientia. 16, 1914, S. 28–59
  • Lorentz, Hendrik Antoon: Deux Memoirs de Henri Poincaré sur la Physique Mathematique. In: Acta Mathematica. 38, 1915/1921, S. 293–308. doi:10.1007/BF02392073 Nachdruck in Poincaré, Oeuvres tome XI, S. 247–261.
  • Maxwell, James Clerk: A Dynamical Theory of the Electromagnetic Field. In: Philosophical Transactions of the Royal Society of London. 155, 1864, S. 459–512
  • Michelson, Albert Abraham: The Relative Motion of the Earth and the Luminiferous Ether. In: American Journal of Science. 22, 1881, S. 120–129
  • Michelson, Albert Abraham & Morley, Edward Williams: On the Relative Motion of the Earth and the Luminiferous Ether. In: American Journal of Science. 34, 1887, S. 333–345
  • Minkowski, Hermann: Das Relativitätsprinzip. In: Jahresbericht der Deutschen Mathematiker-Vereinigung. 1907/1915, S. 372–381
  • Mosengeil, Kurd von: Theorie der stationären Strahlung in einem gleichförmich bewegten Hohlraum. In: Annalen der Physik. 327, Nr. 5, 1907, S. 867–904
  • Palágyi, Menyhért: Neue Theorie des Raumes und der Zeit. Leipzig: Wilhelm Engelmann 1901
  • Planck, Max: Das Prinzip der Relativität und die Grundgleichungen der Mechanik. In: Verhandlungen Deutsche Physikalische Gesellschaft. 8, 1906a, S. 136–141
  • Planck, Max: Die Kaufmannschen Messungen der Ablenkbarkeit der β-Strahlen in ihrer Bedeutung für die Dynamik der Elektronen. In: Physikalische Zeitschrift. 7, 1906b, S. 753–761
  • Planck, Max: Acht Vorlesungen über theoretische Physik, gehalten an der Columbia University in the City of New York. Leipzig: S. Hirzel 1910 Siehe auch englischer Volltext.
  • Poincaré, Henri: Théorie mathématique de la lumière, 1. Paris: G. Carré & C. Naud 1889 Teilweiser Nachdruck des Vorworts in „Wissenschaft und Hypothese“ (1902), Kap. 12.
  • Poincaré, Henri: La mesure du temps. In: Revue de métaphysique et de morale. 6, 1898, S. 1–13, Englisch unter The Measure of Time, Deutsche Übersetzung in „Der Wert der Wissenschaft“ (1905a), Kap. 2.
  • Poincaré, Henri: La théorie de Lorentz et le principe de réaction. In: Archives néerlandaises des sciences exactes et naturelles. 5, 1900, S. 252–278. Siehe auch deutsche Übersetzung.
  • Poincaré, Henri: Sur les principes de la mécanique. In: Bibliothèque du Congrès international de philosophie. 1901, S. 457–494. Nachdruck in „Wissenschaft und Hypothese“ (1902), Kap. 6–7.
  • Poincaré, Henri: Wissenschaft und Hypothese. Berlin: Xenomos 1902/2003, ISBN 3-936532-24-9.
  • Poincaré, Henri: L'état actuel et l'avenir de la physique mathématique. In: Bulletin des sciences mathématiques. 28, Nr. 2, 1904, S. 302-324. Englische Übersetzung in Poincaré, Henri: The Principles of Mathematical Physics. In: Rogers, Howard J. Congress of arts and science, universal exposition, St. Louis, 1904, 1, S. 604–622, Boston and New York: Houghton, Mifflin and Company 1905. Deutsche Übersetzung in „Der Wert der Wissenschaft“ (1905a), Kap. 7–9.
  • Poincaré, Henri: Der Wert der Wissenschaft. Berlin: Xenomos 1905a/2003, ISBN 3-936532-23-0. Siehe auch englischer Volltext.
  • Poincaré, Henri: Sur la dynamique de l'électron. In: Comptes rendus hebdomadaires des séances de l'Académie des sciences. 140, 1905b, S. 1504–1508 Siehe auch deutsche Übersetzung.
  • Poincaré, Henri: Sur la dynamique de l'électron. In: Rendiconti del Circolo matematico di Palermo. 21, 1906, S. 129–176 Siehe auch deutsche Übersetzung.
  • Poincaré, Henri: La dynamique de l'électron. In: Revue générale des sciences pures et appliquées. 19, 1908a, S. 386–402 Nachdruck in Poincaré, Oeuvres, tome IX, S. 551–586; Deutsche Übersetzung in „Wissenschaft und Methode“ (1908), Drittes Buch.
  • Poincaré, Henri: Wissenschaft und Methode. Berlin: Xenomos 1908b/2003, ISBN 3-936532-31-1. Siehe auch englischer Volltext
  • Poincaré, Henri: Letzte Gedanken. Berlin: Xenomos 1913/2003, ISBN 3-936532-27-3 Siehe auch englischer Volltext.
  • Searle, George Frederick Charles: On the Steady Motion of an Electrified Ellipsoid. In: Philosophical Magazine. 44, Nr. 269, 1897, S. 329–341
  • Sommerfeld, Arnold: Zur Relativitätstheorie I: Vierdimensionale Vektoralgebra. In: Annalen der Physik. 337, Nr. 9, 1910, S. 749–776
  • Sommerfeld, Arnold: Zur Relativitätstheorie II: Vierdimensionale Vektoranalyis. In: Annalen der Physik. 338, Nr. 14, 1910, S. 649–689
  • Stokes, George Gabriel: On the Aberration of Light. In: Philosophical Magazine. 27, 1845, S. 9–15
  • Thomson, Joseph John: On the Effects produced by the Motion of Electrified Bodies. In: Philosophical Magazine. 11, 1881, S. 229
  • Tolman, Richard Chase: The mass of a moving body. In: Philosophical Magazine. 23, 1912, S. 375–380
  • Voigt, Woldemar: Über das Doppler’sche Princip. In: Nachrichten von der Königl. Gesellschaft der Wissenschaften und der Georg-Augusts-Universität zu Göttingen. Nr. 2, 1887, S. 41–51
  • Varičak, Vladimir: Zum Ehrenfestschen Paradoxon. In: Physikalische Zeitschrift. 12, 1911, S. 169
  • Wien, Wilhelm: Über die Möglichkeit einer elektromagnetischen Begründung der Mechanik. In: Annalen der Physik. 310, Nr. 7, 1900, S. 501–513. doi:10.1002/andp.19013100703
  • Wien, Wilhelm: Erwiderung auf die Kritik des Hrn. M. Abraham. In: Annalen der Physik. 319, Nr. 8, 1904b, S. 635–637

Sekundärquellen

  • Born, Max: Palagyi, Melchior: Die Relativitätstheorie. In: Die Naturwissenschaften. 3, Nr. 1, 1915
  • Born, Max: Die Relativitätstheorie Einsteins, S. 172-194, Berlin-Heidelberg-New York: Springer 1964/2003, ISBN 3-540-00470-x
  • Boyce Gibson, William Ralph: The Philosophy of Melchior Palagyi. (I) Space-Time and the Criticism of Relativity. In: Journal of Philosophical Studies. 3, Nr. 9, 1928, S. 15–28
  • Darrigol, Olivier: Electrodynamics from Ampére to Einstein. Oxford: Clarendon Press 2000, ISBN 0198505949
  • Einstein, Albert: The Swiss Years: Writings, 1900-1909. In: Stachel, John et al. The Collected Papers of Albert Einstein, 2. Princeton: Princeton University Press 1989, ISBN 0-691-08526-9
  • Fölsing, Albrecht: Albert Einstein. Eine Biographie. Frankfurt am Main: Suhrkamp 1993/1995, ISBN 3518389904
  • Galison, Peter: Einsteins Uhren, Poincarés Karten. Die Arbeit an der Ordnung der Zeit. Frankfurt: Fischer 2003, ISBN 3100244303
  • Giulini, Domenico: Das Problem der Trägheit. In: Preprint, Max-Planck Institut für Wissenschaftsgeschichte. 190, 2001, S. 11–12, 25–26
  • Giulini, Domenico: Über die Herkunft der Speziellen Relativitätstheorie. In: Herbert Hunziker Der jugendliche Einstein und Aarau. Basel: Birkhäuser 2005, ISBN 3764374446, arXiv:physics/0512101v1
  • Goenner, Hubert: On the history of geometrization of space-time. In: 414. Heraeus-Seminar. 2008. arXiv:0811.4529
  • Hentschel, Klaus: Interpretationen und Fehlinterpretationen der speziellen und der allgemeinen Relativitätstheorie durch Zeitgenossen Albert Einsteins. Basel - Boston - Bonn: Birkhäuser 1990, ISBN 3764324384
  • Holton, Gerald: Thematic Origins of Scientific Thought: Kepler to Einstein. Cambridge: Harvard University Press 1973/1988, ISBN 0674877470
  • Katzir, Shaul: Poincaré’s Relativistic Physics: Its Origins and Nature. In: Physics in perspective. 7, 2005, S. 268–292. doi:10.1007/s00016-004-0234-y
  • Miller, Arthur I.: Albert Einstein’s special theory of relativity. Emergence (1905) and early interpretation (1905–1911). Reading: Addison–Wesley 1981, ISBN 0-201-04679-2
  • Pais, Abraham: "Raffiniert ist der Herrgott …": Albert Einstein, eine wissenschaftliche Biographie. Heidelberg: Spektrum 1982/2000, ISBN 3827405297
  • Pauli, Wolfgang: Die Relativitätstheorie. In: Encyclopädie der mathematischen Wissenschaften, 5.2, S. 539–776 1921
  • Schaffner, Kenneth: Nineteenth-century aether theories, S. 99–117 und 255–273, Oxford: Pergamon Press 1972, ISBN 0-08-015674-6
  • Stachel, John: Einstein from "B" to "Z". Boston: Birkhäuser 2002, ISBN 0-8176-4143-2
  • Whittaker, Edmund Taylor: A History of the theories of aether and electricity Vol. 1: The classical theories, 2. Ausgabe, London: Nelson 1951
  • Whittaker, Edmund Taylor: A History of the theories of aether and electricity Vol. 2: The modern theories 1900-1926, 2. Ausgabe, London: Nelson 1953
  • Zahar, Elie: Einstein's Revolution: A Study in Heuristic. Chicago: Open Court Publishing Company 1988/2003, ISBN 0812690672
Nicht-Mainstream
  • Logunov, A.A.: Henri Poincaré and relativity theory. Moskau: Nauka 2004, ISBN 5-02-033964-4, arXiv:physics/0408077

Einzelnachweise

Die in Klammern neben den Namen angegebenen Jahreszahlen verweisen auf das Veröffentlichungsdatum der Primärquelle des jeweiligen Autors. Die Fußnoten verweisen hingegen auf die Sekundärquellen der Wissenschaftshistoriker, welche die inhaltliche Grundlage des Artikels bilden.

  1. ↑ Hentschel (1990), 4f
  2. ↑ Hentschel (1990), 5f
  3. ↑ Hentschel (1990), 10
  4. ↑ Miller (1981); Pais (1982). Kap. 7
  5. ↑ Whittaker (1951), 128ff
  6. ↑ Whittaker (1951), 240ff
  7. ↑ Whittaker (1951), 271ff
  8. ↑ Whittaker (1951), 306ff; (1953) 51f
  9. ↑ Miller (1981), 46
  10. ↑ Miller (1981), 99–100
  11. ↑ Whittaker (1951), 319ff
  12. ↑ Janssen/Stachel (2004), 20
  13. ↑ Miller (1981), 46
  14. ↑ Whittaker (1951), 107ff
  15. ↑ Whittaker (1951), 386f
  16. ↑ Janssen/Stachel (2004), 4–15
  17. ↑ Whittaker (1951), 390f
  18. ↑ Whittaker (1951), 386ff
  19. ↑ Janssen/Stachel (2004), 18–19
  20. ↑ Janssen/Stachel (2004), 19–20
  21. ↑ Miller (1981), 114–115
  22. ↑ a b c Pais (1982), Kap. 6b
  23. ↑ Brown (2001)
  24. ↑ Miller (1981), 27–29
  25. ↑ Janssen (1995), Kap. 3.3
  26. ↑ Janssen (1995), Kap. 3.1
  27. ↑ Macrossan (1986)
  28. ↑ Janssen (1995), Kap. 3.4
  29. ↑ Miller (1981), 113
  30. ↑ Miller (1981), 46, 103
  31. ↑ Darrigol (2005), 18–21
  32. ↑ Janssen/Stachel (2004), 31–32
  33. ↑ Miller (1981), 47–54, 61–67
  34. ↑ Miller (1981), 55–61
  35. ↑ Lange (1886)
  36. ↑ Giulini (2001), Ch. 4
  37. ↑ DiSalle (2002)
  38. ↑ Archibald (1914)
  39. ↑ Goenner (2008)
  40. ↑ Boyce Gibson (1928)
  41. ↑ Born (1915)
  42. ↑ Galison (2003)
  43. ↑ Katzir (2005), 272–275
  44. ↑ Darrigol (2005), 10–11
  45. ↑ Darrigol (2000), 369-372
  46. ↑ Janssen (1995), Kap. 3.3, 3.4
  47. ↑ Miller (1981), Kap. 1, Footnote 57
  48. ↑ Miller (1981), Kap. 1.13
  49. ↑ Miller (1981), 75–79
  50. ↑ Janssen (1995), Kap. 3.4
  51. ↑ Katzir (2005), 275–277
  52. ↑ Janssen/Stachel (2004), 31–32
  53. ↑ Miller (1981), 359–360
  54. ↑ Miller (1981), 79–86
  55. ↑ Brief Nr. 1, Mai 1905
  56. ↑ Brief Nr. 2, Mai 1905
  57. ↑ Janssen (1995), Kap. 3.4
  58. ↑ Katzir (2005), 280–288
  59. ↑ Pais (1982), Kap. 6c
  60. ↑ Walter (2007), Kap. 1
  61. ↑ Darrigol (2005), 15–18
  62. ↑ Janssen (1995), Kap. 4
  63. ↑ Darrigol (2005), 18–21
  64. ↑ Miller (1981), 88
  65. ↑ Miller (1981), 334–352
  66. ↑ Miller (1981), 334–352
  67. ↑ Miller (1981), 329–330
  68. ↑ Pauli (1921), 634–636
  69. ↑ Darrigol (2005), 18–21
  70. ↑ Miller (1981), 359–367
  71. ↑ Janssen (1995), Kap. 3.1
  72. ↑ Miller (1981), 245–253
  73. ↑ a b Norton (2004)
  74. ↑ Stachel (1982)
  75. ↑ Pauli (1921), 549–553
  76. ↑ Born (1964), 326–333
  77. ↑ Bjerknes (2002)
  78. ↑ Miller (1981), Kap. 7.4.6
  79. ↑ a b Walter (1999a), Kap. 3
  80. ↑ Walter (1999a), 49
  81. ↑ Miller (1981), Ch. 12.5.8
  82. ↑ Janssen/Mecklenburg (2007)
  83. ↑ Miller (1981), 257–264
  84. ↑ Pauli (1921), 690–691
  85. ↑ Pauli (1921), 556–557
  86. ↑ Pauli (1921), 555–556
  87. ↑ Miller (1981), 218–219
  88. ↑ a b Walter (1999b)
  89. ↑ Pais (1982), Kap. 12b
  90. ↑ Pais 1982, 11a
  91. ↑ Walter (1999a), Kap. 3
  92. ↑ Whittaker (1953), 27ff
  93. ↑ Holton (1973)
  94. ↑ Miller (1981)
  95. ↑ Pais (1981)
  96. ↑ Katzir (2005)
  97. ↑ Walter (2005)
  98. ↑ Logunov (2004)
  99. ↑ Janssen (1995), Kap. 3.5.4
  100. ↑ Logunov (2004), 28–31
  101. ↑ Miller (1981), 255
  102. ↑ a b Fölsing 1995, Kap. 7
  103. ↑ a b c Miller (1981), Kap. 1.15
  104. ↑ Siehe online.
  105. ↑ J. Renn: Albert Einstein in den Annalen der Physik, 2005
  106. ↑ Holton 1973
  107. ↑ Galison 2003, Kap. 5
  108. ↑ a b Born (1956), 193
  109. ↑ Darrigol (2004), 624
  110. ↑ Fölsing (1995), Kap. 4
  111. ↑ Pais (1982), Kap. 8

Siehe auch

Weblinks


Wikimedia Foundation.

Игры ⚽ Нужно решить контрольную?

Schlagen Sie auch in anderen Wörterbüchern nach:

  • Spezielle Relativitätstheorie (Geschichte) — Unter der Geschichte der speziellen Relativitätstheorie versteht man die Entwicklung von empirischen und konzeptionellen Vorschlägen und Erkenntnissen innerhalb der theoretischen Physik. Diese Entwicklung wurde insbesondere von Hendrik Antoon… …   Deutsch Wikipedia

  • Geschichte der speziellen Relativitätstheorie — Die Geschichte der speziellen Relativitätstheorie bezeichnet zunächst die Entwicklung von empirischen und konzeptionellen Vorschlägen und Erkenntnissen innerhalb der theoretischen Physik, die zu einem neuen Verständnis von Raum und Zeit führten.… …   Deutsch Wikipedia

  • Relativitätstheorie — Die Relativitätstheorie befasst sich mit der Struktur von Raum und Zeit sowie mit dem Wesen der Gravitation. Sie besteht aus zwei maßgeblich von Albert Einstein geschaffenen physikalischen Theorien, der 1905 veröffentlichten speziellen… …   Deutsch Wikipedia

  • Geschichte der Physik — Dieser Artikel wurde den Mitarbeitern der Redaktion Physik zur Qualitätssicherung aufgetragen. Wenn Du Dich mit dem Thema auskennst, bist Du herzlich eingeladen, Dich an der Prüfung und möglichen Verbesserung des Artikels zu beteiligen. Der… …   Deutsch Wikipedia

  • Relativitätstheorie — Re|la|ti|vi|täts|the|o|rie 〈[ vi ] f. 19; unz.〉 von Einstein begründete Theorie zur möglichst allgemeinen Beschreibung der Naturgesetze, aufgrund deren sich auch Raum u. Zeit relativ, d. h. von der Wahl des Bezugssystems abhängig, erweisen * * *… …   Universal-Lexikon

  • Geschichte der Naturwissenschaften — Unter Geschichte der Naturwissenschaften versteht man die Entwicklung der Naturwissenschaften in der Vergangenheit. Das menschliche Erkennen der Natur führte oft zu einem Verwenden der Natur (Naturbeherrschung). Das Potential dazu nahm im Laufe… …   Deutsch Wikipedia

  • Geschichte der Lorentz-Transformation — Die Lorentz Transformation verknüpft wie die Galilei Transformation die Koordinaten x,y,z,t eines Ereignisses in einem bestimmten Inertialsystem mit den Koordinaten x ,y ,z ,t des gleichen Ereignisses in einem anderen Inertialsystem, welches in… …   Deutsch Wikipedia

  • Geschichte der Astronomie — Darstellung des Claudius Ptolemäus mit personifizierter Astronomie aus der Enzyklopädie Margarita Philosophica von Gregor Reisch, 1503. Die Geschichte der Astronomie umfasst zeitlich die gesamte Kulturgeschichte der Menschheit. Die Astronomie… …   Deutsch Wikipedia

  • Geschichte der Kernspaltung — Kaiser Wilhelm Institut für Chemie (heute: Otto Hahn Bau der Freien Universität Berlin) 52.44866613.3429597Koordinaten …   Deutsch Wikipedia

  • Geschichte São Tomés und Príncipes — Die Lage der beiden Hauptinseln im Golf von Guinea Die Geschichte São Tomés und Príncipes bezieht sich auf ein halbes Jahrtausend kolonialer Geschichte dieser Inseln und auf gut drei Jahrzehnte Geschichte des gleichnamigen Staates. Eine… …   Deutsch Wikipedia

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”