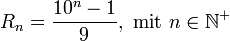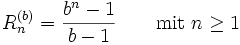Repunitzahl

Der Begriff Repunit ist ein Kunstwort aus den englischen Wörtern repeated (wiederholt) und unit (Einheit) und bezeichnet eine Zahl, die nur die Ziffer 1 enthält. Der Begriff Repunit wurde 1966 von A.H. Beiler geprägt. Im Deutschen wird auch der Begriff Einserkolonne oder Einserschlange verwendet.

Eine prime Repunit oder Repunit-Primzahl ist eine Repunit, die zugleich eine Primzahl ist.

Definition

Mathematisch sind Repunits definiert als

$R_n={10^n-1\over9} ,\ \mbox{mit }n \in \N^{\operatorname +}$

Die Zahl R_n besteht also aus n Einsen. Die Folge der Repunits beginnt 1, 11, 111, 1111, ... (Folge A002275 in OEIS).

Repunit-Primzahlen

Die Definition der Repunits entstand historisch auf der Suche nach einer Zerlegung solcher Zahlen in ihre Primfaktoren. Die Frage, ob eine Repunit-Zahl eine Primzahl ist, beschäftigte im 19. Jahrhundert sogar ernsthafte Mathematiker. So verfasste Carl Gustav Jacob Jacobi eine Arbeit mit dem Titel Untersuchung, ob die Zahl 11111111111 eine Primzahl ist oder nicht. Ein Kuriosum, veranlasst durch Dase.

Es ist einfach zu zeigen, dass R_n durch R_a teilbar ist, falls n durch a teilbar ist. Zum Beispiel ist R₉ teilbar durch R₃: 111111111 = 111 · 1001001. Deshalb muss notwendig n eine Primzahl sein, damit R_n eine Primzahl sein kann. Diese Bedingung ist jedoch nicht hinreichend, zum Beispiel ist R₃ keine Primzahl, da R₃ = 111 = 3 · 37.

Außer für dieses Beispiel von R₃ kann p nur Teiler von R_n sein (für eine Primzahl n), wenn p = 2kn + 1 für ein bestimmtes k.

Repunit-Primzahlen sind selten. R_n ist eine Primzahl für n = 2, 19, 23, 317, 1031, ... (Folge A004023 in OEIS). R₄₉₀₈₁ und R₈₆₄₅₃ sind wahrscheinlich Primzahlen. Es wird vermutet, dass es unendlich viele Repunit-Primzahlen gibt^[1].

Verallgemeinerte Repunits

Da die obige Definition von Repunits auf dem Dezimalsystem beruht, mag diese Definition zunächst willkürlich erscheinen. Man kann die zugrunde liegende Idee jedoch verallgemeinern, indem man Repunits bezüglich einer beliebigen Basis b definiert:

$R_n^{(b)} = {b^n-1\over b-1} \qquad\mbox{mit } n \ge 1$

Die Basis-2-Repunits sind bekannt als die Mersenne-Zahlen M_n = 2ⁿ − 1.

Die Repunit-Primzahlen sind eine Teilmenge der permutierbaren Primzahlen, also der Primzahlen, die Primzahlen bleiben, wenn man ihre Ziffern beliebig vertauscht.

Es ist einfach zu beweisen ^[2], dass für jedes n, das nicht glatt durch 2 oder p teilbar ist, eine Repunit zur Basis 2p existiert, die ein Vielfaches von n ist.

Einzelnachweise

1. ↑ http://primes.utm.edu/glossary/page.php?sort=Repunit
2. ↑ http://www.caliban.org.uk/pmwiki/pmwiki.php?n=Blogs.RichardRothwell.RepUnits

Weblink

• Eric W. Weisstein: Repunit auf MathWorld (englisch)