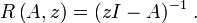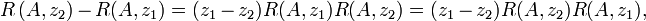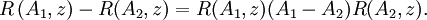Resolventenidentität

In der Mathematik ist die Resolvente die Inverse eines spektral verschobenen linearen Operators oder einer Matrix. Ihr Definitionsbereich ist die Resolventenmenge.

Definition

Für einen linearen Operator A (oder auch eine Matrix 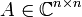$A\in\mathbb{C}^{n\times n}$) definiert man die Resolventenmenge ρ(A) als das Komplement des Spektrums von A, d.h. als die Menge aller komplexen Zahlen z, für die der Operator zI − A beschränkt invertierbar ist. Die Resolventenmenge ist als Komplement des Spektrums offen. Auf der Resolventenmenge definiert man die Resolvente durch

$R\left(A,z\right)=(zI-A)^{-1}\ .$

Viele Autoren verwenden als Definition der Resolvente 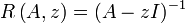$R\left(A,z\right)=(A-zI)^{-1}$, was lediglich ein anderes Vorzeichen bedeutet.

Eigenschaften

Die Resolvente ist eine analytische Funktion und kann auf 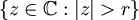$\{z \in \mathbb{C}:|z| > r\}$, wobei r der Spektralradius ist, durch die Neumannsche Reihe dargestellt werden:

$R\left(A,z\right) = \sum_{n = 0}^{\infty} \frac{A^n}{z^{n+1}}$.

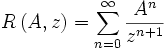Die Resolvente wird verwendet, um Eigenwertentwicklungen von gestörten Operatoren zu beschreiben, z. B. die Entwicklungen von Rellich-Kato und Strutt-Schrödinger.

Resolventenidentitäten

Hilfreich bei Berechnungen sind die erste und zweite Resolventenidentität. Aus 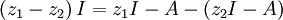$\left(z_1-z_2\right)I=z_1I-A-(z_2I-A)$ folgt mittels Inversion die erste Resolventenidentität

$R\left(A,z_2\right)-R(A,z_1)=(z_1-z_2)R(A,z_1)R(A,z_2) =(z_1-z_2)R(A,z_2)R(A,z_1),$

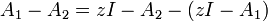und aus $A_1-A_2=zI-A_2-\left(zI-A_1\right)$ folgt mittels Inversion die zweite Resolventenidentität

$R\left(A_1,z\right)-R(A_2,z)=R(A_1,z)(A_1-A_2)R(A_2,z).$