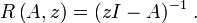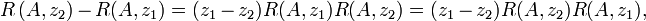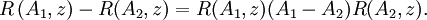Resolvente — In der Mathematik ist die Resolvente die Inverse eines spektral verschobenen linearen Operators oder einer Matrix. Ihr Definitionsbereich ist die Resolventenmenge. Inhaltsverzeichnis 1 Definition 2 Eigenschaften 3 … Deutsch Wikipedia
Resolventenidentität — In der Mathematik ist die Resolvente die Inverse eines spektral verschobenen linearen Operators oder einer Matrix. Ihr Definitionsbereich ist die Resolventenmenge. Definition Für einen linearen Operator A (oder auch eine Matrix ) definiert man… … Deutsch Wikipedia
Holomorphe Halbgruppe — Eine analytische Halbgruppe, manchmal auch holomorphe Halbgruppe genannt, ist eine Familie von beschränkten linearen Operatoren von einem reellen oder komplexen Banachraum X in sich, wobei ein komplexwertiger Sektor und ein Winkel ist.… … Deutsch Wikipedia
Punktspektrum — Das Spektrum eines (linearen) Operators ist ein Begriff aus der Funktionalanalysis, einem Teilgebiet der Mathematik. In der endlichdimensionalen linearen Algebra betrachtet man bei Matrizen und Endomorphismen ihre Eigenwerte. Die… … Deutsch Wikipedia
Satz von Stone — Eine stark stetige Gruppe ist eine Familie von beschränkten linearen Operatoren von einem reellen oder komplexen Banachraum X in sich und ist ein Spezialfall einer stark stetigen Halbgruppe. Stark stetige Gruppen werden bei der Untersuchung von… … Deutsch Wikipedia
Spektraltheorie — Das Spektrum eines (linearen) Operators ist ein Begriff aus der Funktionalanalysis, einem Teilgebiet der Mathematik. In der endlichdimensionalen linearen Algebra betrachtet man bei Matrizen und Endomorphismen ihre Eigenwerte. Die… … Deutsch Wikipedia
Spektrum (Operatortheorie) — Das Spektrum eines (linearen) Operators ist ein Begriff aus der Funktionalanalysis, einem Teilgebiet der Mathematik. In der endlichdimensionalen linearen Algebra betrachtet man bei Matrizen und Endomorphismen ihre Eigenwerte. Die… … Deutsch Wikipedia
Analytische Halbgruppe — Eine analytische Halbgruppe, manchmal auch holomorphe Halbgruppe genannt, ist eine Familie von beschränkten linearen Operatoren von einem reellen oder komplexen Banachraum X in sich, wobei ein komplexwertiger Sektor und ein Winkel ist.… … Deutsch Wikipedia
Fredholmsche Alternative — In der Mathematik ist die nach Ivar Fredholm benannte Fredholm sche Alternative ein Resultat der Fredholmtheorie. Sie kann auf verschiedene Arten ausgedrückt werden: als Theorem der linearen Algebra, als ein Theorem über Integralgleichungen oder… … Deutsch Wikipedia
Infinitesimaler Erzeuger — Eine stark stetige Halbgruppe (gelegentlich auch als C0 Halbgruppe bezeichnet) ist eine Familie von stetigen linearen Abbildungen eines reellen oder komplexen Banachraums X in sich, welche die drei Eigenschaften T(0) = I, T(s + t) = T(s)T(t) für… … Deutsch Wikipedia
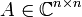 ) definiert man die Resolventenmenge ρ(A) als das Komplement des Spektrums von A, d.h. als die Menge aller komplexen Zahlen z, für die der Operator zI − A beschränkt invertierbar ist. Die Resolventenmenge ist als Komplement des Spektrums offen. Auf der Resolventenmenge definiert man die Resolvente durch
) definiert man die Resolventenmenge ρ(A) als das Komplement des Spektrums von A, d.h. als die Menge aller komplexen Zahlen z, für die der Operator zI − A beschränkt invertierbar ist. Die Resolventenmenge ist als Komplement des Spektrums offen. Auf der Resolventenmenge definiert man die Resolvente durch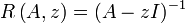 , was lediglich ein anderes Vorzeichen bedeutet.
, was lediglich ein anderes Vorzeichen bedeutet.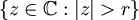 , wobei r der Spektralradius ist, durch die Neumannsche Reihe dargestellt werden:
, wobei r der Spektralradius ist, durch die Neumannsche Reihe dargestellt werden: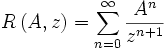 .
.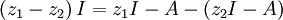 folgt mittels Inversion die erste Resolventenidentität
folgt mittels Inversion die erste Resolventenidentität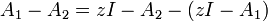 folgt mittels Inversion die zweite Resolventenidentität
folgt mittels Inversion die zweite Resolventenidentität