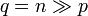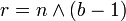Rice-Code

Der Golomb-Code ist eine Darstellungsform für alle positiven ganzen Zahlen einschließlich der Null, im Gegensatz zu anderen Codes, die nur einen endlichen Bereich (z. B. 0-255) darstellen können. Er wurde 1966 von Solomon W. Golomb vorgestellt.

Der Code verwendet wenige Bits für kleine und viele Bits für größere Zahlen. Dabei kann er über einen Parameter gesteuert werden. Je größer der Parameter, desto langsamer wächst die Anzahl der zur Darstellung benötigten Bits, aber desto größer ist die Anzahl der minimal benötigten Bits für die kleinen Zahlen.

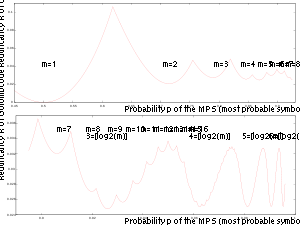
Aufgrund dieser Eigenschaften kann der Code für Entropiekodierungen verwendet werden, bei denen die Wahrscheinlichkeiten der zu kodierenden Zeichen (näherungsweise) eine geometrische Verteilung bilden.

Arbeitsweise

Der Code arbeitet mit der Idee, die darzustellende Zahl durch einen Quotienten q und den Rest r bei einer Division mit einem Parameter b zu ersetzen.

Die Zahl n, mit n > 0 wird durch

$q=\left\lfloor \frac{n}{b} \right\rfloor$

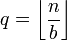
und

$r = n - qb\,$

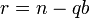
beschrieben. Zur besseren Beschreibung wird noch die Zahl

$c = \left\lceil\log_2 b\right\rceil$

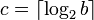
benötigt.

Als erstes wird q + 1 unär ausgegeben, d. h. es werden q "1" Bits gefolgt von einer "0" abgelegt.

Der Rest wird dann in einer "abgeschnittenen binären Darstellung" (en:Truncated_binary_encoding) genannten Codierung abgelegt. Diese Darstellung legt einen Teil der Werte, falls möglich, mit c − 1 Bits und den anderen Teil, mit c Bits ab. Die Anzahl der Werte, die mit c − 1 Bits abgelegt werden kann ist 2^c − b

Beispiele

Die Darstellung der Zahl 10 mit einem Parameter 4:

$q = \left\lfloor\frac{10}{4}\right\rfloor = 2$

$r = 10 - 2 \cdot 4 = 2$

$c = \left\lceil\log_2 4\right\rceil = 2$

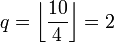
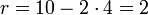
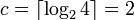
Abhängig von c wird die Codierung vervollständigt:

• falls r < 2^c − b ist, wird r als Binärcode mit der Länge c − 1 geschrieben.

• falls r ≥ 2^c − b ist, wird r + 2^c − b als Binärcode mit der Länge c geschrieben.

Daraus resultiert die Bitfolge "110 10". Das Leerzeichen zeigt den Übergang vom Quotienten zum Rest.

Ein paar weitere Beispiele:

n	0	1	2	3	4	5	6	7	8	9	10
b=3	0 0	0 10	0 11	10 0	10 10	10 11	110 0	110 10	110 11	1110 0	1110 10
b=4	0 00	0 01	0 10	0 11	10 00	10 01	10 10	10 11	110 00	110 01	110 10
b=5	0 00	0 01	0 10	0 110	0 111	10 00	10 01	10 10	10 110	10 111	110 00
b=7	0 00	0 010	0 011	0 100	0 101	0 110	0 111	10 00	10 010	10 011	10 100

Anwendung

Die beiden Grafiken zeigen die Redundanz des Golomb-Code pro Symbol. Auf der Abszisse ist die Auftretenswahrscheinlichkeit des häufigeren Symbols ablesbar.

Der Golomb-Code kann angewendet werden, wenn Zahlen unbekannter Größe abspeichert werden sollen.

Das eigentliche Anwendungsgebiet liegt in der Datenkompression. Wenn die Wahrscheinlichkeiten der Zahlen eine bestimme Verteilung (geometrische Verteilung) aufweisen, dann kann der Golomb-Code ähnlich effizient wie der Huffman-Code sein, ist dabei aber sparsamer mit Speicher, leichter zu implementieren und schneller in der Ausführung.

Rice-Code

Der Rice-Code ist eine Variante des Golomb-Codes, bei dem der Parameter b eine Potenz von 2 ist. Diese Codes lassen sich sehr einfach mit Bitshiften und logischen Bitoperationen umsetzen.

Angenommen, es gilt b = 2^p. Dann ist

$q = n \gg p$

und

$r = n \and (b-1)$

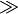$\gg$ steht dabei für bitweises Verschieben nach rechts und 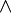$\and$ für bitweise Und-Verknüpfung.

r wird dabei immer mit genau p Bits dargestellt.

Literatur

Golomb S. W., Run-Length Encodings, IEEE Transactions on Information Theory IT-12(3):399-401