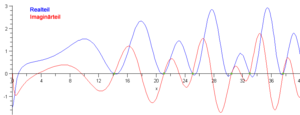
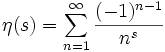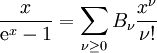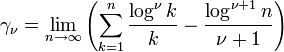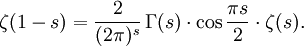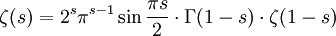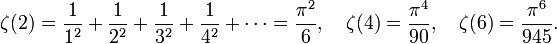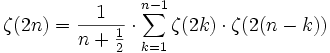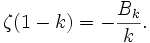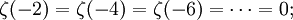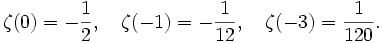- Riemannsche Zetafunktion
-
Die riemannsche ζ-Funktion (nach Bernhard Riemann) ist eine Funktion, die in der analytischen Zahlentheorie, einem Teilgebiet der Mathematik, eine wichtige Rolle spielt. Ihre Bedeutung liegt darin, dass ihre Nullstellen im Komplexen Auskunft über Primzahlen, deren Verteilung und viele derer Eigenschaften geben. Zudem ist sie eine bedeutende Dirichlet-Reihe, die in vielen Disziplinen Anwendungen hat.
Inhaltsverzeichnis
Definition
Für komplexe Zahlen
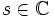 , deren Realteil größer als 1 ist, ist die Zetafunktion definiert durch
, deren Realteil größer als 1 ist, ist die Zetafunktion definiert durch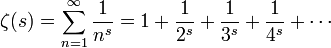 .
.
Andere Ausdrücke für die ζ-Funktion
liefert für
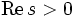 und
und 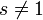 den Ausdruck
den Ausdruck .[1]
.[1]
Die ζ-Funktion lässt sich aufgrund der eindeutigen Zerlegung natürlicher Zahlen in Primzahlen für
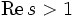 auch als Produkt (Euler-Produkt) schreiben:
auch als Produkt (Euler-Produkt) schreiben:Zur Integraldarstellung für
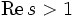 ,
,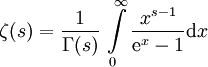 ,
,
wobei Γ die Gamma-Funktion ist, gelangt man über eine Transformation unter Zuhilfenahme der Bernoulli-Zahlen Bk, die über die Beziehung
definiert sind.[1] Zerlegt man das Integral in die beiden Intervalle
![[0,\,1]](/pictures/dewiki/51/3c677f273d5640cb290c4e4ac717fbc7.png) und
und ![[1,\,\infty]](/pictures/dewiki/101/e51b2bd8f42f13c14bfb3e408b346551.png) , erhält man die Summenformel
, erhält man die Summenformel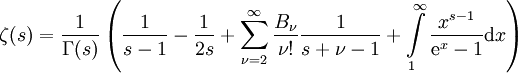 ,
,
wobei Bν die oben definierten Bernoulli-Zahlen sind.
Darstellung für die komplexe Zahlenebene
Hierfür greift man auf die Euler-MacLaurin-Summenformel,
![\sum\limits_{n=2}^{N} f(n) = \int\limits_1^N f(x)\,dx\,
+\,\sum\limits_{\nu=1}^q (-1)^\nu\,\frac{B_\nu}{\nu!}\,\left(f^{(\nu-1)}(N)-f^{(\nu-1)}(1)\right)\,
-\,\frac{(-1)^q}{q!}\int\limits_1^N B_q(x-[x])\,f^{(q)}(x)\,dx](/pictures/dewiki/54/67fdffdcba22e869c064aa0df2b46731.png) ,
,
zurück, wobei f als Mindestvoraussetzung eine auf dem Intervall [1,N] q-mal differenzierbare Funktion ist, Bν(x) die Bernoulli-Polynome sind und [x] den ganzzahligen Anteil von x darstellt.[2] Indem man
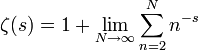 mit der Summenformel umwandelt, erhält man den Ausdruck
mit der Summenformel umwandelt, erhält man den Ausdruck![\zeta(s) =
\frac{1}{s-1}\,+\,\frac{1}{2}\,
+\,\sum\limits_{\nu=2}^q\frac{B_\nu}{\nu!}\,\prod\limits_{k=0}^{\nu-2}(s+k)\,
-\,\frac{1}{q!}\,\prod\limits_{k=0}^{q-1}(s+k)\,\int\limits_1^\infty B_q(x-[x])\,x^{-(s+q)}\,dx](/pictures/dewiki/97/ac2da2dbb7ac1b89b9b328f10f6a1390.png) .
.
Diese Formel gilt nicht nur für die Ebene
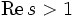 , sondern sogar für
, sondern sogar für  (wobei natürlich wieder
(wobei natürlich wieder 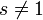 sei). Durch die freie Wahl von
sei). Durch die freie Wahl von 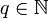 kann man den Definitionsbereich beliebig ausdehnen und hat damit einen Ausdruck für ganz
kann man den Definitionsbereich beliebig ausdehnen und hat damit einen Ausdruck für ganz  .[2]
.[2]Die zugehörige Laurentreihe hat die Form
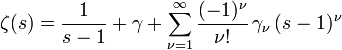 ;
;
dabei ist γ = γ0 die Euler-Mascheroni-Konstante und bei den Koeffizienten
handelt es sich um die verallgemeinerten Euler-Konstanten.[1]
Funktionalgleichung
Auf ganz
 gilt als Identität zwischen meromorphen Funktionen
gilt als Identität zwischen meromorphen FunktionenEine andere Darstellung ist
für alle s in
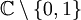 .
.Spezielle Werte
Gerade natürliche Zahlen
Für eine positive ganze Zahl n ist
Beispielsweise ist
Diese Formeln wurden von Euler entdeckt und 1735 in seiner Arbeit De Summis Serierum Reciprocarum erstmals veröffentlicht. Das Auffinden des Werts von ζ(2) ist auch als das Basler Problem bekannt.
Daneben gibt es auch eine höchst bemerkenswerte Rekursionsformel
für natürliche Zahlen
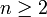 , die allerdings Euler noch nicht bekannt war.[3]
, die allerdings Euler noch nicht bekannt war.[3]Die Wahrscheinlichkeit, dass eine zufällig gewählte Zahl quadratfrei ist, ist gleich
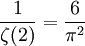 , genauer: Die Wahrscheinlichkeit, dass zwei zufällig gewählte Zahlen kleiner als N teilerfremd sind, konvergiert für
, genauer: Die Wahrscheinlichkeit, dass zwei zufällig gewählte Zahlen kleiner als N teilerfremd sind, konvergiert für 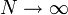 gegen diesen Wert.[4]
gegen diesen Wert.[4]Ungerade natürliche Zahlen
Über den Wert der Zetafunktion für ungerade natürliche Zahlen ist nur sehr wenig bekannt. Beispielsweise weiß man, dass die Apéry-Konstante ζ(3) irrational ist.
Nichtpositive ganze Zahlen
Für eine ganze Zahl k > 0 gilt
Über die Funktionalgleichung ist diese Formel äquivalent zur oben angegebenen Formel für die Werte auf den geraden natürlichen Zahlen. Da Bk = 0 für ungerade k, gilt insbesondere
weitere Werte sind
Halbzahlige Argumente
Auch die Werte für halbzahlige Argumente sind interessant, und zwar gilt
- ζ(1 / 2) = − 1,4603545088095868…,
- ζ(3 / 2) = 2,6123753486854883….
Dieser Wert wird nämlich in der Physik bei der Berechnung der kritischen Temperatur für die Ausbildung eines sog. Bose-Einstein-Kondensats und in der Spinwellen-Theorie bei magnetischen Systemen benötigt.
- ζ(5 / 2) = 1,3414872572509171…,
- ζ(7 / 2) = 1,1267338673170566….
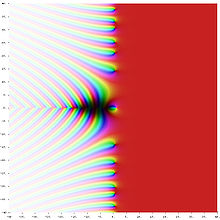
Nullstellen der Zetafunktion
Aus der Produktdarstellung kann man leicht folgern, dass
 für
für 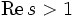 gilt. Zusammen mit der Funktionalgleichung ergibt sich, dass die einzigen Nullstellen außerhalb des kritischen Streifens
gilt. Zusammen mit der Funktionalgleichung ergibt sich, dass die einzigen Nullstellen außerhalb des kritischen Streifensdie „trivialen“ Nullstellen
 sind.
sind.Die Lage der Nullstellen im kritischen Streifen hängt eng mit Aussagen über die Verteilung der Primzahlen zusammen. Beispielsweise ist die Aussage, dass auf dem Rand des kritischen Streifens keine Nullstellen liegen, ein möglicher Zwischenschritt beim Beweis des Primzahlsatzes. Weitere Vergrößerungen des „nullstellenfreien Bereiches“ implizieren Restgliedabschätzungen im Primzahlsatz. Riemann vermutete im Jahr 1859, dass alle Nullstellen auf der parallel zur imaginären Achse verlaufenden Geraden
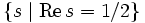 liegen. Diese so genannte riemannsche Vermutung konnte bislang weder bewiesen noch widerlegt werden.
liegen. Diese so genannte riemannsche Vermutung konnte bislang weder bewiesen noch widerlegt werden.Der Verlauf der Zeta-Funktion in der komplexen Ebene, besonders entlang von parallel zur imaginären Achse verlaufenden Streifen, wird wegen des Zusammenhangs mit der Primzahlverteilung und des davon unmittelbar betroffenen sog. "Faktorisierungsproblems" seit kurzem auch gezielt mit physikalischen Methoden untersucht, und zwar mit Interferenz-Methoden analog zur Holographie. Man teilt dazu die definierende Summe in zwei Teile mit positiver bzw. negativer Phase auf, ψ bzw. ψ*, die man anschließend zur Interferenz bringt. [5]
Literatur
Zur Mathematik:
- Jürgen Neukirch: Algebraische Zahlentheorie. Springer, Berlin 1992, ISBN 3-540-54273-6.
- Harold Edwards Riemann´s Zetafunction, Dover 2001, ISBN 0486417409
- Edward Charles Titchmarsh: The Theory of the Riemann Zeta-Function. 1951.
- Don Zagier: Zetafunktionen und quadratische Körper. Springer, Berlin; Heidelberg; New York 1981, ISBN 3-540-10603-0 (Teil 1, insbesondere § 4).
- Eugen Jahnke: Tafeln höherer Funktionen. Teubner, Stuttgart 1966.
Zur Geschichte:
- Marcus du Sautoy: Die Musik der Primzahlen. Auf den Spuren des größten Rätsels der Mathematik. 4 Auflage. Beck, München 2005, ISBN 3-406-52320-X.
Einzelreferenzen
- ↑ a b c Dragan Miličić: Notes on Riemann's Zeta Function.
- ↑ a b Hans Rademacher: Topics in Analytic Number Theory. Springer-Verlag Berlin et al. 1973, ISBN 3-540-05447-2.
- ↑ Reinhold Remmert: Funktionentheorie I. Springer-Verlag Berlin et al. 1984, ISBN 3-540-12782-8, Seite 234.
- ↑ Julian Havil: Gamma. Springer-Verlag Berlin et al. 2007, ISBN 978-3-540-48495-0, Seite 79.
- ↑ Siehe z. B. W. Merkel et al., Factorization of Numbers with Physical Systems, in "Elements of Quantum Information" (Hrsg. W.P. Schleich und H. Walther), Wiley-VCH-Verlag, Weinheim 2007, Seite 339 bis 353
Siehe auch
- Dedekindsche Zeta-Funktion
- Hurwitzsche Zetafunktion
Weblinks
Die folgenden Arbeiten sind englisch, aktuell und verschaffen einen schnellen Überblick:
- Xavier Gourdon, Pascal Sebah: Definition
- Xavier Gourdon, Pascal Sebah: Allgemeines
- Xavier Gourdon, Pascal Sebah: Numerische Berechnung
- Xavier Gourdon, Pascal Sebah: Nullstellen
- P. Cerone: Bounds for Zeta and Related Functions. Journal of Inequalities in Pure and Applied Mathematics, Band 6, Nr. 5, 2005 (enthält Abschätzungen der Zetafunktion für ungerade n)
- Funktionswerte für
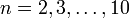
Wikimedia Foundation.