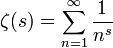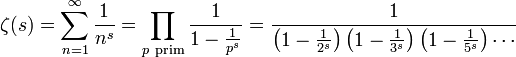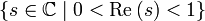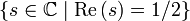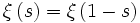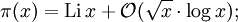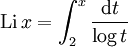Riemann'sche Vermutung

Die riemannsche Vermutung oder riemannsche Hypothese (nach Bernhard Riemann) ist eine Annahme über die Nullstellen der riemannschen Zetafunktion. Sie besagt, dass alle nichttrivialen Nullstellen dieser komplexwertigen Funktion den Realteil ½ besitzen. Ob die Vermutung zutrifft oder nicht, ist eines der bedeutendsten ungelösten Probleme der Mathematik.

Die riemannsche Zetafunktion

Betrag der Zetafunktion auf der kritischen Geraden Re(s) = 1/2

Funktionswerte der Zetafunktion auf der kritischen Geraden Re(s) = 1/2

Die riemannsche Zetafunktion ist eine komplexwertige Funktion, die durch die folgende Reihe definiert ist:

$\zeta (s) = \sum_{n=1}^{\infty} \frac{1}{n^s} \qquad$

Dabei ist die Variable 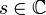$s \in \mathbb{C}$ komplexwertig. Die Darstellung gilt nur für Realteile 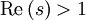$\mathrm{Re}\,(s) >1$, die Funktion lässt sich aber auf die gesamte komplexe Ebene mit Ausnahme von s = 1 eindeutig analytisch fortsetzen. Im Punkt s = 1 besitzt sie einen einzigen einfachen Pol.

Eine der wichtigsten Eigenschaften der riemannschen Zetafunktion ist ihr Zusammenhang mit den Primzahlen. Sie stellt eine Beziehung zwischen komplexer Analysis und analytischer Zahlentheorie her und bildet den Ausgangspunkt der riemannschen Vermutung. Der folgende Ausdruck stellt den Zusammenhang formelhaft dar als

$\zeta (s) = \sum_{n=1}^{\infty}\frac{1}{n^s}= \prod_{p\ \text{prim}} \frac{1}{1-\frac1{p^s}} = \frac1{\left(1-\frac1{2^s}\right) \left(1-\frac1{3^s}\right)\left(1-\frac1{5^s}\right)\cdots}$

wobei Π_p ein unendliches Produkt über alle Primzahlen p darstellt. Der Ausdruck folgt unmittelbar aus dem Satz über die Eindeutigkeit der Primzahlzerlegung und der Summationsformel für die Geometrische Reihe.

Riemannsche Vermutung

Riemannsche Zetafunktion in der komplexen Ebene, horizontal Re(s) und vertikal Im(s). Eine Reihe weißer Flecken markiert die Nullstellen bei Re(s) = ½. Für eine vollständige Darstellung des Vorschaubildes hier klicken.

Die Zetafunktion besitzt die auf ganz 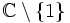$\mathbb C \setminus \{1\}$ gültige meromorphe Darstellung:

$\zeta (s)=\frac{1}{\Gamma (s)} \left(\frac{1}{s-1}-\frac{1}{2s}+\sum\limits_{n =2}^\infty \frac{B_n}{n !}\frac{1}{s+n-1}+\int\limits_1^\infty \frac{x^{s-1}}{e^x-1} \mathrm dx \right)$,

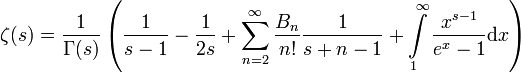wobei Γ die Gamma-Funktion und B_n die Bernoulli-Zahlen sind.

Anmerkung: Bei der hier verwendeten Definition der Bernoulli-Zahlen gilt:

$B_0=1,\; B_1=-1/2,\; B_2=1/6,\; B_3=0, \dots$

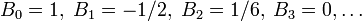
Die Zeta-Funktion hat triviale Nullstellen, die sich aus der Menge der Polstellen der Gamma-Funktion vermindert um die Menge der Polstellen des Klammerausdrucks durch Aufhebung ergeben. Es handelt sich dabei um die Menge der negativen geraden Zahlen $s = -2,\; -4, \; -6, \dots$.

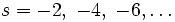Eine zentrale Erkenntnis Riemanns in seiner berühmten Arbeit aus dem Jahre 1859 war die Feststellung, dass sich alle möglichen nichttrivialen Nullstellen in dem Streifen

$\{s\in\mathbb C \mid 0 < \mathrm{Re}\,(s) < 1 \}$

befinden müssen.

Die berühmte – und bis heute weder widerlegte noch bewiesene – Vermutung von Bernhard Riemann besagt, dass alle nichttrivialen Nullstellen auf der mittleren Geraden

$\{s\in\mathbb C \mid \mathrm{Re}\,(s) = 1/2 \}$

liegen.

Riemann kam auf seine Vermutung bei der Untersuchung des Produkts der Zetafunktion mit der Gammafunktion

$\xi(s) = \pi^{- \frac {s} {2}} \; \Gamma \left( \frac {s} {2} \right) \zeta (s)$,

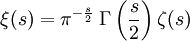die bei der Vertauschung von s mit (1 − s) invariant ist, das heißt, sie erfüllt die Funktionalgleichung:

$\xi \left( s \right) = \xi \left( 1-s \right)$

Die Gerade in der komplexen Zahlenebene mit dem Realteil 1/2 ist bei dieser Spiegelung ebenfalls invariant.

Bedeutung

Aus der riemannschen Vermutung folgt beispielsweise eine Restgliedabschätzung im Primzahlsatz:

$\pi(x) = \mathrm{Li}\,x+\mathcal{O}(\sqrt x\cdot\log x);$

dabei ist

$\mathrm{Li}\,x=\int_2^x\frac{\mathrm dt}{\log t}$

der Integrallogarithmus. Viele weitere Resultate der analytischen Zahlentheorie, aber auch etwa für die in der Kryptographie wichtigen schnellen Primzahltests, können bisher nur unter Annahme der Riemannhypothese bewiesen werden. In den komplexen Nullstellen der Zetafunktion sind, wie Michael Berry schrieb, die Fluktuationen um die grobe asymptotisch logarithmische Verteilung der Primzahlen, die der Primzahlsatz beschreibt, kodiert. Kennt man die genaue Verteilung, kann man auch genauere Aussagen über die Wahrscheinlichkeit treffen, wie viele Primzahlen in einem Bereich anzutreffen sind.

Die eigentliche Ursache dafür, dass viele Mathematiker so intensiv nach einer Lösung gesucht haben, ist aber — abgesehen davon, dass dies die letzte noch unbewiesene Aussage in Riemanns berühmtem Aufsatz ist — dass sich in dieser außergewöhnlich perfekten Symmetrie einer ansonsten sehr chaotischen Funktion (z. B. Universalitätssatz von Voronin (en): die Zetafunktion kann jede beliebige analytische von Null verschiedene Funktion innerhalb eines Kreises vom Radius 1/4 beliebig approximieren) wahrscheinlich die Spitze des Eisbergs einer fundamentalen Theorie verbirgt, so wie sich hinter der Fermatvermutung die Parametrisierung von elliptischen Kurven durch Modulfunktionen verbarg, ein Teil des Langlands-Programms.

Geschichte

Die riemannsche Vermutung wurde schon 1859 von Bernhard Riemann in einer berühmten Arbeit, die die Grundlagen der analytischen Zahlentheorie legte, nur nebenbei erwähnt, da sie, wie er schrieb, für den unmittelbaren Fortgang der Untersuchung seines Aufsatzes nicht wesentlich wäre. Er sicherte seine Vermutung ab durch umfangreiche numerische Berechnung der Nullstellen, wie Carl Ludwig Siegel in den 1930er Jahren bei Untersuchung von Riemanns Nachlass herausfand. Das Problem wurde im Jahr 1900 von David Hilbert in seiner Liste der 23 mathematischen Probleme als Jahrhundertproblem deklariert. 1903 veröffentlichte Jørgen Pedersen Gram die ersten 15 im kritischen Bereich liegenden Nullstellen. Sie unterstützen (beweisen aber nicht) die riemannsche Vermutung, ebenso wie alle weiteren Nullstellen, die später gefunden wurden und deren Anzahl Anfang der achtziger Jahre die 100-Millionen-Grenze überschritt. Im Jahr 2001 wurde mit Hilfe von Großrechnern gezeigt, dass die ersten zehn Milliarden Nullstellen der komplexen Zeta-Funktion alle die riemannsche Vermutung erfüllen, d. h., sie liegen alle auf der Geraden mit Realteil 1 / 2.

Einen weiteren Meilenstein bei der numerischen Suche stellte das im August 2001 gestartete Zeta-Grid-Projekt dar. Mit Hilfe der Methode des verteilten Rechnens, an der viele Tausend Internet-Nutzer teilnahmen, wurden nach drei Jahren etwa 1 Billion Nullstellen gefunden. Das Projekt wurde inzwischen eingestellt.

Die beiden französischen Mathematiker Gourdon und Demichel starteten mit dem Verfahren von Odlyzko und Schönhage im Jahr 2004 einen neuen Versuch und hatten im Oktober 2004 die ersten 10 Billionen Nullstellen überprüft, ohne ein Gegenbeispiel zu finden.

Da im 20. Jahrhundert kein Beweis für die riemannsche Vermutung gefunden wurde, hat das Clay Mathematics Institute im Jahr 2000 dieses Vorhaben erneut zu einem der wichtigsten mathematischen Probleme erklärt und einen Preis von einer Million US-Dollar auf einen schlüssigen Beweis ausgesetzt, allerdings nicht für ein Gegenbeispiel.

Im Juni 2004 hat Louis de Branges de Bourcia zum wiederholten Male einen angeblichen Beweis veröffentlicht, der derzeit kritisch geprüft wird. Bereits Jahre zuvor hat Eberhard Freitag jedoch ein Gegenbeispiel für eine im Beweis aufgestellte Behauptung gezeigt, so dass der Beweis mittlerweile als falsch angesehen wird.

Verwandte Vermutungen

In der analytischen Zahlentheorie gibt es weitere Vermutungen, die mit der riemannschen Vermutung in Beziehung stehen. Die mertenssche Vermutung besagt, dass 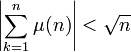$\left| \sum_{k=1}^n \mu(n)\right| < \sqrt{n}$ für alle n > 1. Dabei ist μ(n) die Möbiusfunktion. Die mertenssche Vermutung ist stärker als die riemannsche Vermutung, wurde jedoch 1985 widerlegt^[1].

Die lindelöfsche Vermutung über die Ordnung der Zetafunktion entlang der kritischen Geraden ist schwächer als die riemannsche Vermutung, aber immer noch unbewiesen.

Jeffrey Lagarias stellte 1992 eine zur Riemannvermutung äquivalente Vermutung der elementaren Zahlentheorie auf.

Beweisideen aus der Physik

Neue Ideen für den Beweis der Vermutung kamen aus der Physik. Schon David Hilbert und George Polya war aufgefallen, dass die Riemann-Hypothese folgen würde, falls die Nullstellen Eigenwerte eines Operators (1/2 + i T) wären, wobei T ein hermitescher (das heißt selbstadjungierter) Operator ist, der also nur reelle Eigenwerte hat, ähnlich wie die Hamiltonoperatoren in der Quantenmechanik. In den 1970er Jahren fand dann Hugh Montgomery bei einer Unterhaltung mit Freeman Dyson, dass die Verteilung der (normalisierten) Abstände aufeinanderfolgender Nullstellen eine ähnliche Verteilung wie die Eigenwerte unitärer Zufallsmatrizen zeigte, was Andrew Odlyzko durch numerische Rechnungen bestätigte. In den 1990er-Jahren begannen dann auch Physiker wie Michael Berry nach einem solchen zugrundeliegenden System zu suchen, etwa in der Theorie des Quantenchaos. Weitere Unterstützung finden diese Überlegungen in einer Analogie der „expliziten Formeln“ in der Theorie der riemannschen Zetafunktion mit der Selberg-Spurformel, die die Eigenwerte des Laplace-Beltrami-Operators auf einer Riemannfläche mit den Längen der geschlossenen Geodäten in Beziehung setzt, und der Gutzwiller-Spurformel in der Quantenchaos-Theorie. Diese verbindet die Eigenwerte (Energien) der quantenmechanischen Version eines chaotischen klassischen Systems mit den Längen der periodischen Bahnen im klassischen Fall. Bei all diesen Spurformeln (trace formulas) handelt es sich um Identitäten zwischen den Summen der jeweiligen Nullstellen, Bahnkurven-Periodenlängen, Eigenwerte usw.

Ein vom Fields-Medaillen-Preisträger Alain Connes 1996 im Rahmen seiner „nicht-kommutativen Geometrie“ angegebener Operator passt „fast“. Connes konnte aber bisher nicht die Existenz weiterer Nullstellen außerhalb der kritischen Geraden ausschließen.

Eine weitere Idee aus der Physik, die in Zusammenhang mit der Riemannvermutung diskutiert wurde, sind die „Yang-Lee-Nullstellen“ der ins Komplexe analytisch fortgesetzten Zustandssumme in Modellen der statistischen Mechanik. Chen Ning Yang und Tsung-Dao Lee bewiesen unter Verwendung eines Resultats von George Polya aus der Theorie der Zetafunktion, auf das sie Mark Kac aufmerksam machte, dass in bestimmten Modellen die Nullstellen auf einem Kreis lagen, bei anderen Modellen liegen sie auf einer Geraden. Die Lage der Nullstellen bestimmt das Verhalten in Phasenübergängen ähnlich, wie die Nullstellen auf der kritischen Geraden die Feinverteilung der Primzahlen steuern.

All diesen Ideen liegt eine Analogie zugrunde, die sich vereinfacht etwa so beschreiben lässt: Die Primzahlen sind „Elementarteilchen“, die über die Multiplikation in Wechselwirkung treten und so die zusammengesetzten Zahlen aufbauen. Gleichzeitig werden die „Teilchen“ durch die Addition angeordnet. In der Zetafunktion werden nun in Form einer Summen- bzw. Produktformel beide Aspekte (additiv/natürliche Zahlen und multiplikativ/Primzahlen) miteinander verbunden.

Eine Verbindung der Riemann-Vermutung zu eindimensionalen Quasikristallen schlug Freeman Dyson 2009 vor.^[2]

Einzelnachweise

1. ↑ A. M. Odlyzko and H. J. J. te Riele: Disproof of the Mertens conjecture, J. reine angew. Math., 357 (1985), pp. 138-160, Online-Version
2. ↑ Dyson „Birds and Frogs“, Notices AMS 2009, PDF-Datei

Literatur

• Marcus du Sautoy: Die Musik der Primzahlen. Auf den Spuren des größten Rätsels der Mathematik. dtv/C.H. Beck, München 2003, 2004. ISBN 3-423-34299-4 (populäre Darstellung der Geschichte der Vermutung)
• John Derbyshire: Prime obsession - Bernhard Riemann and the greatest unsolved problem in Mathematics. Washington 2003. ISBN 0-309-08549-7
• Harold M. Edwards: Riemann's Zeta Function. New York 1974, Dover 1991. ISBN 0-486-41740-9
• Edward Charles Titchmarsh: The Theory of the Riemann Zeta-Function. Bearbeitet von Heath-Brown. Oxford 1987. ISBN 0198533691

Weblinks

• ZetaGrid Projekt
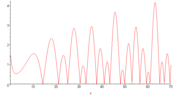
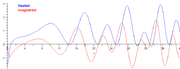
• Grafiken der Riemannschen Zeta-Funktion
• Graph der Riemannschen Zeta-Funktion (Animation)
• The 10^13 first zeros of the Riemann Zeta function, and zeros computation at very large height von Xavier Gourdon
• Matthew Watkins Webseiten zu Zusammenhängen mit der Physik, viele gute links
• Connes Trace formula in non commutative geometry and the zeros of the Riemann zeta function 1998
• Clay Mathematics Institute zur Riemannschen Vermutung mit Faksimile von Riemanns Arbeit und Bombieris Beschreibung
• MathWorld-Artikel zur riemannschen Vermutung (englisch)
• Übersichtsartikel zur Riemannschen Vermutung von Peter Sarnak