Ringsummen-Normalform

Die Ringsummennormalform (kurz RSNF) (auch: Reed-Muller-Entwicklung oder Ringsummenexpansion) ist eine Darstellungsform einer Booleschen Funktion. Diese Normalform verwendet ausschließlich die Operatoren XODER (Kontravalenz) und UND (Konjunktion).

Definition

Die beiden Operatoren Kontravalenz und Konjunktion 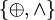$\{\oplus,\wedge\}$ bilden eine vollständig Basis der booleschen Funktionen. Damit wird die folgende Definition möglich.

Eine Formel ist in Ringsummennormalform, wenn sie eine Kontravalenz (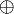$\oplus$) von Konjunktionen (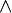$\wedge$) der Eingabevariablen x₁,...,x_n und der Konstanten 0,1 ist. Eine Formel in RSNF hat folgende Form:

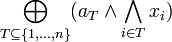$\bigoplus_{T\subseteq\{1,...,n\}} ( a_T \wedge \bigwedge_{i\in T} x_i )$, wobei 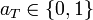$a_T\in\{0,1\}$ für jede Teilmenge T ist.

Beispiel

Die Formel 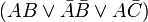$(AB \vee \bar{A} \bar{B} \vee A \bar{C})$ kann umgeformt werden in ihre RSNF: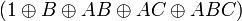

$(1 \oplus B \oplus A B \oplus A C \oplus A B C)$

Folgerungen

• Jede beliebige boolesche Funktion kann in Ringsummennormalform überführt werden.
• Die Ringsummennormalform einer booleschen Funktion ist eindeutig.

Literatur

• Ingo Wegener: The complexity of Boolean functions. Wiley-Teubner, 1987, ISBN 3-519-02107-2, S. 6 (Online-Ausgabe)