Rolling-Ball-Rotation

Physikalische Interpretation der Rolling-Ball-Rotation

Die Rolling-Ball-Rotation („Rotation des rollenden Balls“, auch Rollerball-Rotation) ist eine Mensch-Computer-Interaktionstechnik, die es erlaubt, mit Hilfe eines normalen Zeigegeräts dreidimensionale Rotationen eines Objekts in alle Richtungen durchzuführen. Sie ist in vielen 3D-Modellierungs- und CAD-Werkzeugen eingebaut.

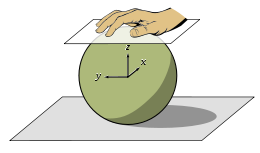
Bei der Rolling-Ball-Rotation wird an einem beliebigen Punkt eine Maustaste gedrückt, der Mauszeiger verschoben und die Maustaste wieder losgelassen. Die dadurch bestimmte Rotation ist die einer Kugel, die ohne zu gleiten auf einer flachen Oberfläche rollt und die von oben mit der flachen Hand entsprechend der Bewegung des Mauszeigers bewegt wird.

Die Rolling-Ball-Rotation ist kontextfrei, das heißt, die Rotation wird vollständig durch den Verschiebungsvektor des Mauszeigers definiert, ohne dass frühere Positionen in die Drehung mit einfließen.

Umsetzung

Folgende Drehmatrix drückt die Rotation in Abhängigkeit von der Verschiebung des Mauszeigers aus:

$\begin{pmatrix} \cos \theta+(dy/dr)^2(1-\cos \theta) & -(dx/dr)(dy/dr)(1-\cos \theta) & (dx/dr)\sin \theta\\ \\ -(dx/dr)(dy/dr)(1-\cos \theta) & \cos \theta + (dx/dr)^2(1-\cos \theta) & (dy/dr)\sin \theta\\ \\ -(dx/dr)\sin \theta & -(dy/dr)\sin \theta & \cos \theta \end{pmatrix}$

dx und dy geben die Verschiebung des Mauszeigers in der X- beziehungsweise Y-Richtung in Pixeln an. Die anderen Werte sind wie folgt definiert:

$dr = \sqrt{dx^2+dy^2}$

$\cos \theta = \frac{R}{\sqrt{R^2+dr^2}}$

$\sin \theta = \frac{dr}{\sqrt{R^2+dr^2}}$

R ist dabei ein frei wählbarer Parameter, der den Radius des virtuellen rollenden Balls angibt und somit die Empfindlichkeit der Rotation bestimmt. Üblich ist ein Wert in der Größenordnung von 100 Pixeln.

Die Matrix ist so definiert, dass die X-, Y- und Z-Achsen ein rechtshändiges Koordinatensystem ergeben. Ihre Anwendung geht davon aus, dass sich das Rotationszentrum am Ursprung befindet. Wird eine Rotation um einen anderen Punkt gewünscht, so ist vorher und nachher eine entsprechende Verschiebung anzuwenden. Außerdem muss die Rotation auf ein Mal durchgeführt werden; nacheinander erfolgende Rotationen um die verschiedenen Achsen ergeben nicht dasselbe Resultat.

Weitere Interaktionsmethoden

Weitere, kontextsensitive Interaktionsmethoden zur Kontrolle der Rotation sind die Arcball-Methode von Shoemake^[1] oder Chens Virtual Sphere^[2].

Literatur

• Andrew J. Hanson: The rolling ball. In David Kirk (Hrsg.): Graphics Gems III, S. 51–60, Academic Press, San Diego 1992, ISBN 0-12-409671-9 (Online, Gzipped PostScript)
• Andrew J. Hanson: Rotations for N-Dimensional Graphics. In Alan W. Paeth (Hrsg.): Graphics Gems V, S. 55–64, Morgan Kaufmann, San Diego 1995, ISBN 0-12-543457-X (Online, PDF)

Weitere Methoden:

1. ↑ Ken Shoemake: Arcball rotation control. In Paul Heckbert (Hrsg.): Graphics Gems IV. S. 172–192. Academic Press, Boston 1994, ISBN 0-12-336155-9
2. ↑ Michael Chen u. a.: A Study in Interactive 3-D Rotation Using 2-D Control Devices. In SIGGRAPH 1988 Proceedings. S. 121–130. ACM, New York 1988, ISBN 0-89791-275-6 (Online, PDF)