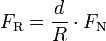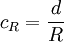Rollwiderstandsbeiwert

Der Rollwiderstand (auch: Rollreibung oder rollende Reibung) entspricht dem Verformungswiderstand eines sich abwälzenden Körpers.

Als Kennwert wird der Rollwiderstandskoeffizient c_R (auch: Rollwiderstandsbeiwert, Rollreibungsbeiwert usw.) angegeben.

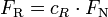$F_{\rm R} = c_{R} \cdot F_{\rm N}$  – Rollwiderstand ist Rollwiderstandskoeffizient mal Normalkraft

Die Werte für die Rollwiderstandskoeffizienten sind verglichen mit den passenden Werten für Gleitreibung erheblich kleiner. Daher haben Wälzlager (z. B. Kugellager) gegenüber Gleitlagern in Bezug auf Reibung Vorteile.

Der Rollwiderstandskoeffizient c_R hängt neben der Material-Paarung auch von der Geometrie (Radius des Rollköpers) und der Normalkraft F_N ab. Dies ist im Gegensatz zur Coulomb'schen Reibung (Haft- oder Gleitreibung), wo der Widerstandskoeffizienten fast ausschließlich von der Materialpaarung bestimmt ist.

Die Kraft, die überwunden werden muss, um einen Körper (beispielsweise ein Rad) aus dem Stillstand in rotierende Bewegung zu versetzen, wird als Anfahrwiderstand bezeichnet.

Grundlagen

Asymmetrische Kontaktkraft

Kräfte während des Rollens

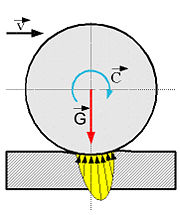
Beim Abrollen werden sowohl der rollende Körper als auch die Unterlage (die Fahrbahn) verformt. Die Verformung erfolgt sowohl an dem Wälzkörper selbst als auch an der Wälzkörperbahn und zwar am Berührungspunkt oder an der Berührungslinie. In der Regel ist dies eine elastische Verformung.

• Ein alltägliches Beispiel ist die Kombination Radkranz-Schiene bei der Eisenbahn. Das Material der Schiene wird hier so gewählt, dass sie stärker verformt wird als das Rad. Hier wird auch deutlich, dass der Zug (auch bei horizontaler Schiene) ständig leicht "bergauf fahren" muss, damit er aus dem Tal der Eindruckstelle herauskommt.
• Ein weiteres alltägliches Beispiel ist die Kombination Reifen-Fahrbahnbelag. Hier ist die Verformung beim Reifen sichtbar größer als bei der (befestigten) Straße. Ein erhöhter Luftdruck im Reifen mindert folglich den Rollwiderstand. Dies hat jedoch negative Auswirkungen hinsichtlich Lenkfähigkeit und beim Bremsvorgang. Daher ist ein Kompromiss erforderlich. Typisch dafür ist der Unterschied zwischen Sommer- und Winterreifen.

Häufig kommt es infolge der Dauerbelastung zu einer Materialermüdung und Teile werden herausgelöst. Das ist die sogenannte Grübchenbildung (englisch: Pitting).

Mathematische Behandlung

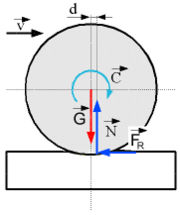
Durch die Verformung beim Abrollen wird die Kontaktkraft zwischen Körper und Unterlage asymmetrisch (Fig.1). Der Ersatz der Kontaktkräfte durch statisch äquivalente Einzelkräfte ergibt eine Normalkraft F_N, welche um die Strecke d nach vorne verschoben ist, und eine Reibungskraft F_R entgegen der Bewegungsrichtung (Fig.2).

Aus den Gleichgewichtsbedingungen folgt für Rollen bei konstanter Geschwindigkeit

$F_{\rm R} = \frac{d}{R} \cdot F_{\rm N}$

Die Reibungskraft F_R ist direkt vom Radius R des rollenden Körpers abhängig, große Räder rollen also leichter. Im Gegensatz dazu hat bei der Haft- oder der Gleitreibung die Größe der Körper keinen Einfluss.

Die Länge d wird auch Hebelarm der Rollreibung oder Rollreibungslänge genannt. Es ist offensichtlich, dass diese Länge von der Größe des Rollkörpers wie auch von der Belastung abhängt.

Rollwiderstandskoeffizient

Der Quotient 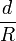$\frac{d}{R}$ ist der Rollwiderstandskoeffizient c_R (veraltet auch: Rollwiderstandsbeiwert, Rollreibungsbeiwert):

$c_{R} = \frac{d}{R}$

Damit bekommt der Ausdruck für die Rollreibung F_R die Form

$F_{\rm R} = c_{R} \cdot F_{\rm N}$

Der Rollwiderstandskoeffizient ist eine dimensionslose (einheitenfreie) Zahl, die von Materialeigenschaften und Geometrie der abrollenden Körpers sowie von der Belastung im Kontaktbereich abhängt. Typische Zahlenwerte des Rollwiderstandskoeffizienten liegen um ein bis über zwei Größenordnungen unter denen des Gleitreibungskoeffizienten.

Typische Rollwiderstandskoeffizienten c_R

cR	Wälzkörper/Wälzkörperbahn
0,0005–0,001	Kugellager, Kugel und Lager aus gehärtetem Stahl4
0,001–0,002	Eisenbahnrad auf Schiene1
0,007	Fahrradreifen auf Asphalt
0,006–0,010	Autoreifen auf Asphalt, Lkw
0,011–0,015	Autoreifen auf Asphalt, Pkw
0,01–0,02	Autoreifen auf Beton2
0,020	Autoreifen auf Schotter
0,015–0,03	Autoreifen auf Kopfsteinpflaster2
0,03–0,06	Autoreifen auf Schlaglochstrecke2
0,045	Verbinderkette (Raupenfahrwerk, Leopard 2) auf fester Fahrbahn
0,050	Autoreifen auf Erdweg
0,04–0,08	Autoreifen auf festgefahrenem Sand2
0,07–0,08	Gurtband (Raupenfahrwerk, Caterpillar Challenger und John Deere 8000T) auf Asphalt
0,2–0,4	Autoreifen auf losem Sand2/3

¹ Gustav Niemann gibt für Eisenbahnräder folgende (aus Versuchen ermittelte) Formel an: 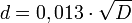$d = 0,013 \cdot \sqrt{D}$; d und D in mm. Bei 800 mm Raddurchmesser ergibt sich ca. 0,4 mm, was einem Koeffizienten von 0,001 entspricht.

² Quelle: Schmidt, Schlender 2003

³ Wer schon einmal versucht hat, am Strand Fahrrad zu fahren, kann diese hohen Zahlenwerte aus eigener Anschauung bestätigen

⁴ Quelle: Dubbel: Taschenbuch für den Maschinenbau

Grenzen der Theorie

Die oben beschriebene Beziehung 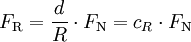$F_{\rm R}= \frac{d}{R} \cdot F_{\rm N} = c_{R} \cdot F_{\rm N}$ ist ein vereinfachtes Modell, welches für die meisten Berechnungen in der Technik ausreichend ist. Die Abhängigkeit der Reibung von weiteren Größen (Kontaktkraft, Geschwindigkeit, etc.) wird hierbei nicht berücksichtigt.

Ferner betrachtet das beschriebene Modell nicht den möglichen Einfluss eines dritten Stoffes, der an der Grenzschicht zwischen Wälzkörper und Wälzkörperbahn vorhanden sein kann (Flüssigkeit oder Schmierstoff). Beispiele sind Schmierfett auf der Schiene oder Glatteis auf der Straße. In einem solchen Fall wird von Mischreibung gesprochen.

Extreme Werte für Geschwindigkeiten und Temperaturen sowie eventuell chemische Einflüsse an den Kontaktstellen können mit diesem Modell nicht erfasst werden.

Gedankenexperiment

Vollkommen starre Körper haben auch unter Belastung keine Verformung. Solche Körper gibt es real nicht.

Nimmt man dennoch in Gedanken an, die Eisenbahnräder und die Schiene seien vollkommen starr. Dann kann der Zug ohne Reibung rollen. Beim Beschleunigen wird es schwierig, die Haftgrenze nicht zu überschreiten, da sonst die Räder durchdrehen - die Haftreibung ist aber auch in diesem Fall nicht Null, wie oft laienhaft postuliert wird.

Fazit: Die Verformung an der Kontaktstelle bringt mehr Rollwiderstand, aber auch mehr Haftung. Aus diesem Grund sind die Reifen in der Formel 1 weich, die Kugeln in Kugellagern sehr hart.

Weiterführende Informationen

• T. Schmidt, D.Schlender (2003): Untersuchung zum saisonalen Reifenwechsel unter Berücksichtigung technischer und klimatischer Aspekte
• Popov, Valentin L.: Kontaktmechanik und Reibung. Ein Lehr- und Anwendungsbuch von der Nanotribologie bis zur numerischen Simulation, Springer-Verlag, 2009, 328 S., ISBN 978-3-540-88836-9.

Weblinks

• Rollversuche zur Ermittlung des Rollwiderstandes