Rot-Schwarz-Baum

Ein Rot-Schwarz-Baum ist in der Informatik eine vom binären Suchbaum abgeleitete Datenstruktur, die sehr schnellen Zugriff auf die in ihr gespeicherten Werte garantiert. Rot-Schwarz-Bäume wurden zuerst 1972 von Rudolf Bayer beschrieben^[1], welcher sie symmetric binary B-trees nannte. Der heutige Name geht auf Leo J. Guibas und Robert Sedgewick zurück, die 1978 die rot-schwarze Farbkonvention einführten.^[2] Die schnellen Zugriffzeiten auf die einzelnen im Rot-Schwarz-Baum gespeicherten Elemente werden durch fünf Eigenschaften erreicht, die zusammen garantieren, dass ein Rot-Schwarz-Baum immer balanciert ist, wodurch die Höhe eines Rot-Schwarz-Baumes mit n Werten nie größer wird als 2log ₂(n + 1). Somit können die wichtigsten Operationen in Suchbäumen – suchen, einfügen und löschen – garantiert in O(log n) ausgeführt werden.

Eigenschaften

Ein Rot-Schwarz-Baum ist ein binärer Suchbaum, in dem jeder Knoten eine Zusatzinformation – seine Farbe – trägt. Neben den Bedingungen, die an binäre Suchbäume gestellt werden, wird an Rot-Schwarz-Bäume jedoch noch die Forderung gestellt, folgende fünf Eigenschaften immer zu erfüllen:

1. Jeder Knoten im Baum ist entweder rot oder schwarz.
2. Die Wurzel des Baums ist schwarz.
3. Alle Blatt-Knoten (NIL) sind schwarz.
4. Ist ein Knoten rot, so sind beide Kinder schwarz.
5. Jeder Pfad von einem gegebenen Knoten zu seinen Blattknoten enthält die gleiche Anzahl schwarzer Knoten (Schwarzhöhe/Schwarztiefe).

Beispiel eines Rot-Schwarz-Baumes

Durch diese fünf Bedingungen wird die wichtigste Eigenschaft von Rot-Schwarz-Bäumen sichergestellt: Die Anzahl der Knoten auf dem längsten Pfad von der Wurzel zu einem Blatt ist nie mehr als doppelt so hoch wie die Anzahl der Knoten des kürzesten Pfades von der Wurzel zu einem Blatt. Hierdurch ist ein Rot-Schwarz-Baum immer annähernd balanciert, was für die Operationen suchen, einfügen und löschen wichtig ist, da deren Laufzeitkosten proportional zur Höhe des Baumes sind. Da die Höhe eines Rot-Schwarz-Baumes dadurch, dass er annähernd balanciert ist, minimiert wird, wird somit ebenfalls die Laufzeit der oben genannten Operationen minimiert. Somit kann man für Rot-Schwarz-Bäume eine obere Schranke für die Laufzeit der Operationen suchen, einfügen und löschen garantieren.

Um zu verstehen, warum diese fünf Eigenschaften eine obere Schranke für die Laufzeit garantieren, reicht es sich zu verdeutlichen, dass aufgrund der vierten Eigenschaft auf keinem Pfad zwei rote Knoten aufeinander folgen dürfen, weswegen sich auf dem längsten Pfad immer ein roter Knoten mit einem schwarzen Knoten abwechselt, während auf dem kürzesten Pfad nur schwarze Knoten vorhanden sind. Da die fünfte Eigenschaft jedoch festlegt, dass die Anzahl der schwarzen Knoten auf allen Pfaden gleich sein muss, kann der Pfad, auf dem sich jeweils ein roter mit einem schwarzen Knoten abwechselt, maximal doppelt so lang sein wie der Pfad, auf dem nur schwarze Knoten sind. Einen formalen Beweis für diese Eigenschaft des Rot-Schwarz-Baumes findet man unter Höhenbeweis weiter unten im Artikel.

Anmerkung: Während es auch möglich ist, Binärbäume zu betrachten, bei denen die Knoten nicht immer genau zwei Kinder haben müssen, betrachtet dieser Artikel der Einfachheit halber nur Bäume, welche immer genau zwei Kinder haben. Hierzu werden eventuell fehlende Kinder als schwarzes Blatt ohne Suchschlüssel (sog. NIL-Blatt) eingeführt. Somit sind alle Knoten mit Suchschlüssel innere Knoten (und haben genau zwei Kinder) und alle Blätter NIL-Knoten. (siehe hierzu auch den Beispielbaum)

Operationen

Suchen

Die Suchoperation erben Rot-Schwarz-Bäume von den allgemeinen binären Suchbäumen. Für eine genaue Beschreibung des Algorithmus siehe dort.

Einfügen

Das Einfügen in den Rot-Schwarz-Baum funktioniert wie das Einfügen in einen binären Suchbaum, wobei der neue Knoten rot gefärbt wird, damit die Schwarztiefe des Baumes erhalten bleibt. Nach dem Einfügen können jedoch eventuell die zweite oder – was wahrscheinlicher ist – die vierte Eigenschaft des Rot-Schwarz-Baumes verletzt sein, weswegen es nötig werden kann, den Baum zu reparieren. Hierbei unterscheidet man insgesamt fünf Fälle, welche im Folgenden genauer betrachtet werden.

Anmerkung: Wenn im folgenden von Vater (parent), Großvater (grandparent) und Onkel (uncle) die Rede ist, so sind diese jeweils relativ zum neu einzufügenden Knoten (N) zu sehen.

Zur Verdeutlichung wird bei jedem der fünf Fälle ein Stück C-Code angegeben, welches zeigt, wie der entstandene Baum repariert wird.

Den Großvater bzw. den Onkel eines Knotens kann man wie folgt bestimmen:

 node grandparent(node n) {
     return n->parent->parent;
 }
 
 node uncle(node n) {
     if (n->parent == grandparent(n)->left)
         return grandparent(n)->right;
     else
         return grandparent(n)->left;
 }

Fall 1: Der neu eingefügte Knoten ist die Wurzel des Baumes.

Da hierdurch die zweite Eigenschaft verletzt wird (Die Wurzel des Baums ist schwarz) färbt man die Wurzel einfach um. Da dieser Fall nur eintritt, falls man ein Element in den leeren Baum einfügt, braucht man sich nicht um weitere Reparaturen zu kümmern, da es im Baum nach dem Einfügen nur diesen einen Knoten gibt, weswegen keine der weiteren Eigenschaften verletzt werden kann.

 void insert_case1(node n) {
     if (n->parent == NULL)
         n->color = BLACK;
     else
         insert_case2(n);
 }

Fall 2: Der Vater des neuen Knotens ist schwarz.

Hierdurch könnte die fünfte Eigenschaft gefährdet sein, da der neue Knoten selbst wieder zwei schwarze NIL-Knoten mitbringt und somit die Schwarztiefe auf einem der Pfade um eins erhöht wird.

Da der eingefügte Knoten selbst aber rot ist, und beim Einfügen einen schwarzen NIL-Knoten verdrängt hat, bleibt die Schwarztiefe auf allen Pfaden erhalten und es ist nichts zu tun.

 void insert_case2(node n) {
     if (n->parent->color == BLACK)
         return; /* Alle Eigenschaften des Baumes sind immer noch gewahrt */
     else
         insert_case3(n);
 }

Anmerkung: In den nun folgenden Fällen kann angenommen werden, dass der einzufügende Knoten einen Großvater hat, da sein Vater rot ist, und somit nicht selbst die Wurzel sein kann (Die Wurzel des Baums ist schwarz). Da es sich aber bei einem Rot-Schwarz-Baum um einen Binärbaum handelt, hat der Großvater auf jeden Fall noch ein Kind (auch wenn es sich bei diesem um einen NIL-Knoten handeln kann).

Fall 3: Sowohl Onkel als auch Vater des neuen Knotens sind rot Fall 3: Sowohl der Onkel als auch der Vater des neuen Knotens sind rot. In diesem Fall kann man beide Knoten einfach schwarz färben, und im Gegenzug den Großvater rot färben, wodurch die fünfte Eigenschaft wiederhergestellt wird. Durch diese Aktion wird das Problem um ein Level nach oben verschoben, da durch den nun rot gefärbten Großvater die zweite oder vierte Eigenschaft verletzt sein könnte, weswegen nun der Großvater betrachtet werden muss. Dieses Vorgehen wird solange rekursiv fortgesetzt, bis keine der Regeln mehr verletzt wird.

 void insert_case3(node n) {
     if (uncle(n) != NULL && uncle(n)->color == RED) {
         n->parent->color = BLACK;
         uncle(n)->color = BLACK;
         grandparent(n)->color = RED;
         insert_case1(grandparent(n));
     }
     else
         insert_case4(n);
 }

Anmerkung: In den beiden noch verbleibenden Fällen wird der Einfachheit halber angenommen, dass der Vaterknoten das linke Kind seines Vaters (also des Großvaters des einzufügenden Knotens) ist. Sollte er das rechte Kind seines Vaters sein, so müssen in den beiden folgenden Fällen jeweils links und rechts vertauscht werden. Der Beispielcode berücksichtigt diesen Fall bereits.

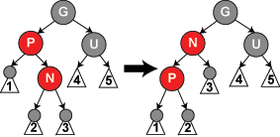
Fall 4: Der neue Knoten hat einen schwarzen Onkel und ist das rechte Kind seines roten Vaters. Der Vater hängt links am Großvater. Fall 4: Der neue Knoten hat einen schwarzen oder keinen Onkel und ist das rechte Kind seines roten Vaters während der Vater jedoch links am Großvater sitzt. In diesem Fall kann man eine Linksrotation um den Vater ausführen, welche die Rolle des einzufügenden Knotens und seines Vaters vertauscht. Danach kann man den ehemaligen Vaterknoten mit Hilfe des fünften Falles bearbeiten. Durch die oben ausgeführte Rotation wurde ein Pfad (im Bild mit 1 markiert) so verändert, dass er nun durch einen zusätzlichen Knoten führt, während ein anderer Pfad (im Bild mit 3 markiert) so verändert wurde, dass er nun einen Knoten weniger hat. Da es sich jedoch in beiden Fällen um rote Knoten handelt, ändert sich hierdurch an der Schwarztiefe nichts, womit die fünfte Eigenschaft erhalten bleibt.

 void insert_case4(node n) {
     //knoten ist rechts am vater und vater links am großvater
     if (n == n->parent->right && n->parent == grandparent(n)->left) {
         rotate_left(n->parent);
         n = n->left;
     //knoten ist links am vater und vater rechts am großvater
     } else if (n == n->parent->left && n->parent == grandparent(n)->right) {
         rotate_right(n->parent);
         n = n->right;
     }
     insert_case5(n);
 }

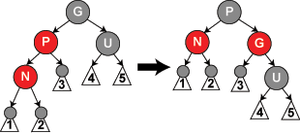
Fall 5: Der neue Knoten hat einen schwarzen Onkel und ist das linke Kind seines roten Vaters. Der Vater hängt links am Großvater. Fall 5: Der neue Knoten hat einen schwarzen oder keinen Onkel und ist das linke Kind seines roten Vaters; der Vater hängt auch links am Großvater. In diesem Fall kann man eine Rechtsrotation um den Großvater ausführen, wodurch der ursprüngliche Vater nun der Vater von sowohl dem neu einzufügenden Knoten als auch dem ehemaligen Großvater ist. Da der Vater rot war, muss nach der vierten Eigenschaft (Kein roter Knoten hat ein rotes Kind) der Großvater schwarz sein. Vertauscht man nun die Farben des ehemaligen Großvaters bzw. Vaters, so ist in dem dadurch entstehenden Baum die vierte Eigenschaft wieder gewahrt. Die fünfte Eigenschaft bleibt ebenfalls gewahrt, da alle Pfade, die durch einen dieser drei Knoten laufen, vorher durch den Großvater liefen und nun alle durch den ehemaligen Vater laufen, der inzwischen – wie der Großvater vor der Transformation – der einzige schwarze der drei Knoten ist.

 void insert_case5(node n) {
     n->parent->color = BLACK;
     grandparent(n)->color = RED;
     //knoten ist links am vater und vater links am großvater
     if (n == n->parent->left && n->parent == grandparent(n)->left) {
         rotate_right(grandparent(n));
     //knoten ist rechts am vater und vater rechts am großvater
     } else {
         /* Ab hier gilt, n == n->parent->right und n->parent == grandparent(n)->right */
         rotate_left(grandparent(n));
     }
 }

Löschen

Illustration der beiden Möglichkeiten den Knoten mit dem Wert 7 aus dem Binärbaum zu löschen Das Löschen eines Knotens aus einem Rot-Schwarz-Baum erfolgt analog zum Löschen eines Knotens aus binären Bäumen. Falls der zu löschende Knoten zwei Kinder hat (keine NIL-Knoten), so sucht man entweder den maximalen Wert im linken Teilbaum oder den minimalen Wert im rechten Teilbaum des zu löschenden Knotens, kopiert diesen Wert in den eigentlich zu löschenden Knoten, und entfernt den gefundenen Knoten aus dem Rot-Schwarz-Baum. Da der gefundene Knoten maximal ein Kind besitzen kann, da sein Wert sonst nicht maximal oder minimal gewesen wäre, lässt sich das Problem so auf das Löschen eines Knotens mit maximal einem Kind vereinfachen.

Anmerkung: Im Folgenden werden wir also nur noch Knoten mit maximal einem echten Kind betrachten, und dieses Kind als 'sein Kind' bezeichnen. Falls der Knoten gar keine echten Kinder hat, soll einer der beiden NIL-Knoten die Rolle des Kindes spielen.

Will man einen roten Knoten löschen, so kann man diesen durch sein Kind ersetzen, welches nach der vierten Eigenschaft (Kein roter Knoten hat ein rotes Kind) schwarz sein muss. Da der Vater des gelöschten Knotens ebenfalls aufgrund derselben Eigenschaft schwarz gewesen sein muss, wird die vierte Eigenschaft somit nicht mehr verletzt. Da alle Pfade, die ursprünglich durch den gelöschten roten Knoten verliefen, nun durch einen roten Knoten weniger verlaufen, ändert sich an der Schwarztiefe ebenfalls nichts, und die fünfte Eigenschaft (Die Anzahl der schwarzen Knoten von jedem beliebigen Knoten zu einem Blatt ist auf allen Pfaden gleich) bleibt auch erhalten.

Ebenfalls noch einfach zu lösen ist der Fall, wenn der zu löschende Knoten schwarz ist, aber ein rotes Kind hat. Würde in diesem Fall einfach der schwarze Knoten gelöscht werden, könnte dadurch sowohl die vierte als auch die fünfte Eigenschaft verletzt werden. Das kann jedoch umgangen werden, indem das Kind schwarz gefärbt wird. Somit treffen garantiert keine zwei roten Knoten aufeinander (der eventuell rote Vater des gelöschten Knotens und sein rotes Kind) und alle Pfade, die durch den gelöschten schwarzen Knoten verliefen, verlaufen nun durch sein schwarzes Kind, wodurch beide Eigenschaften erhalten bleiben.

Die oben angegebene Löschung eines Knotens mit einem Kind kann durch das folgende Programm realisiert werden, das den Knoten n mittels replace_node durch den Knoten child ersetzt.

 void delete_one_child(node n) {
     /* Vorbedingung: n hat höchstens ein echtes Kind (kein NIL-Knoten) */
     node child = is_leaf(n->right) ? n->left : n->right;
     replace_node(n, child);
     if (n->color == BLACK) {
         if (child->color == RED)
             child->color = BLACK;
         else
             delete_case1(child);
     }
     free(n);
 }

Anmerkung: Der Code setzt voraus, dass eventuelle NIL-Knoten durch tatsächliche Knoten repräsentiert werden und nicht einfache Nullzeiger sind.

Schwieriger zu lösen ist der Fall, wenn sowohl der zu löschende Knoten als auch sein Kind schwarz sind. Zuerst ersetzt man den zu löschenden Knoten mit seinem Kind, und löscht danach den Knoten. Nun verletzt jedoch dieser nachgerückte Kind-Knoten, im folgenden Konfliktknoten genannt, die Eigenschaften eines Rot-Schwarz-Baumes, da es nun einen Pfad gibt, welcher vorher durch zwei schwarze Knoten führte, jetzt aber nur noch durch einen führt. Somit ist die fünfte Regel (Die Anzahl der schwarzen Knoten von jedem beliebigen Knoten zu einem Blatt ist auf allen Pfaden gleich) verletzt. Je nach Ausgangslage werden nun sechs verschiedene Fälle unterschieden, wie der Baum wieder zu reparieren ist, die im Folgenden genauer betrachtet werden.

Anmerkung: Wenn im folgenden von Vater (parent), Bruder (sibling), Großvater (grandparent) und Onkel (uncle) die Rede ist, so sind diese jeweils relativ zum Konfliktknoten zu sehen. Diesen Konfliktknoten selbst bezeichnen wir in den Diagrammen mit N. Zur Verdeutlichung wird bei jedem der Fälle ein Stück C-Code angegeben, das zeigt, wie der entstandene Baum repariert wird.

Den Bruder (sibling) eines Knotens kann man wie folgt bestimmen:

 node sibling(node n) {
      if (n == n->parent->left)
          return n->parent->right;
      else
          return n->parent->left;
 }

Fall 1: Der Konfliktknoten (N) ist die neue Wurzel. In diesem Fall ist man fertig, da ein schwarzer Knoten von jedem Pfad entfernt wurde und die neue Wurzel schwarz ist, womit alle Eigenschaften erhalten bleiben.

 void delete_case1(node n) {
     if (n->parent == NULL)
         return;
     else
         delete_case2(n);
 }

Anmerkung: Für die Fälle 2, 5 und 6 sei der Konfliktknoten (N) das linke Kind seines Vaters. Sollte er das rechte Kind sein, so müssen in den drei Fällen jeweils links und rechts vertauscht werden. Der Beispielcode berücksichtigt diesen Fall bereits.

Fall 2: Der Bruder (S) des Konfliktknotens (N) ist rot. Fall 2: Der Bruder (S) des Konfliktknotens ist rot. In diesem Fall kann man die Farben des Vaters und des Bruders des Konfliktknotens invertieren und anschließend eine Linksrotation um seinen Vater ausführen, wodurch der Bruder des Konfliktknotens zu dessen Großvater wird. Alle Pfade haben weiterhin dieselbe Anzahl an schwarzen Knoten, aber der Konfliktknoten hat nun einen schwarzen Bruder und einen roten Vater, weswegen man nun zu Fall 4, 5, oder 6 weitergehen kann.

 void delete_case2(node n) {
     if (sibling(n)->color == RED) {
         n->parent->color = RED;
         sibling(n)->color = BLACK;
         if (n == n->parent->left)
             rotate_left(n->parent);
         else
             rotate_right(n->parent);
     }
     delete_case3(n);
 }

Fall 3: Der Vater (P) des Konfliktknotens (N), sein Bruder (S) und die Kinder seines Bruders (SL oder SR) sind schwarz Fall 3: Der Vater (P) des Konfliktknotens, sein Bruder (S) und die Kinder seines Bruders (SL oder SR) sind alle schwarz. In diesem Fall kann man einfach den Bruder rot färben, wodurch alle Pfade die durch diesen Bruder führen – welches genau die Pfade sind, die nicht durch den Konfliktknoten selbst führen – einen schwarzen Knoten weniger haben, wodurch die ursprüngliche Ungleichheit wieder ausgeglichen wird. Jedoch haben alle Pfade, die durch den Vater laufen, nun einen schwarzen Knoten weniger als jene Pfade die nicht durch den Vater laufen, wodurch die fünfte Eigenschaft immer noch verletzt wird. Um dies zu reparieren, versucht man nun den Vaterknoten zu reparieren, indem man versucht, einen der sechs Fälle – angefangen bei Fall 1 – anzuwenden.

 void delete_case3(node n) {
     if (n->parent->color == BLACK &&
         sibling(n)->color == BLACK &&
         sibling(n)->left->color == BLACK &&
         sibling(n)->right->color == BLACK)
     {
         sibling(n)->color = RED;
         delete_case1(n->parent);
     }
     else
         delete_case4(n);
 }

Fall 4: Sowohl der Bruder (S) des Konfliktknotens (N) als auch die Kinder des Bruders (SL oder SR) sind schwarz, aber der Vater (P) des Konfliktknotens ist rot Fall 4: Sowohl der Bruder des Konfliktknotens als auch die Kinder des Bruders (SL bzw. SR) sind schwarz, aber der Vater (P) des Konfliktknotens rot. In diesem Fall reicht es aus, die Farben des Vaters und des Bruders zu tauschen. Hierdurch bleibt die Anzahl der schwarzen Knoten auf den Pfaden, die nicht durch den Konfliktknoten laufen, unverändert, fügt aber einen schwarzen Knoten auf allen Pfaden, die durch den Konfliktknoten führen, hinzu, und gleicht somit den gelöschten schwarzen Knoten auf diesen Pfaden aus.

 void delete_case4(node n) {
     if (n->parent->color == RED &&
         sibling(n)->color == BLACK &&
         sibling(n)->left->color == BLACK &&
         sibling(n)->right->color == BLACK)
     {
         sibling(n)->color = RED;
         n->parent->color = BLACK;
     }
     else
         delete_case5(n);
 }

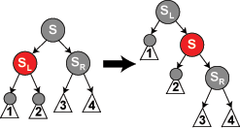
Fall 5: Das linke Kind (SL) des Bruders (S) ist rot, das rechte Kind (SR) wie auch der Bruder (S) des Konfliktknotens (N) sind jedoch schwarz und der Konfliktknoten selbst ist das linke Kind seines Vaters (P) Fall 5: Das linke Kind (SL) des Bruders (S) ist rot, das rechte Kind (SR) wie auch der Bruder des Konfliktknotens (N) sind jedoch schwarz und der Konfliktknoten selbst ist das linke Kind seines Vaters. In diesem Fall kann man eine Rechtsrotation um den Bruder ausführen, sodass das linke Kind (SL) des Bruders dessen neuer Vater wird, und damit der Bruder des Konfliktknotens wird. Danach vertauscht man die Farben des Bruders und seines neuen Vaters. Nun haben alle Pfade immer noch die gleiche Anzahl an schwarzen Knoten, aber der Konfliktknoten hat einen schwarzen Bruder dessen rechtes Kind rot ist, womit man nun zum sechsten Fall weitergehen kann. Weder der Konfliktknoten selbst noch sein Vater werden durch diese Transformation beeinflusst.

 void delete_case5(node n) {
     if (n == n->parent->left &&
         sibling(n)->color == BLACK &&
         sibling(n)->left->color == RED &&
         sibling(n)->right->color == BLACK)
     {
         sibling(n)->color = RED;
         sibling(n)->left->color = BLACK;
         rotate_right(sibling(n));
     }
     else if (n == n->parent->right &&
              sibling(n)->color == BLACK &&
              sibling(n)->right->color == RED &&
              sibling(n)->left->color == BLACK)
     {
         sibling(n)->color = RED;
         sibling(n)->right->color = BLACK;
         rotate_left(sibling(n));
     }
     delete_case6(n);
 }

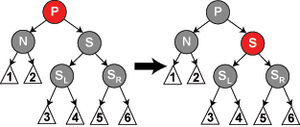
Fall 6: Der Bruder (S) des Konfliktknotens (N) ist schwarz, das rechte Kind des Bruders (SR) rot und der Konfliktknoten selbst ist das linke Kind seines Vaters Fall 6: Der Bruder (S) des Konfliktknotens (N) ist schwarz, das rechte Kind des Bruders (SR) rot und der Konfliktknoten selbst ist das linke Kind seines Vaters. In diesem Fall kann man eine Linksrotation um den Vater des Konfliktknotens ausführen, sodass der Bruder der Großvater des Konfliktknotens, und der Vater seines ehemaligen rechten Kindes (SR) wird. Nun reicht es die die Farben des Bruders und des Vaters des Konfliktknotens zu tauschen und das rechte Kind des Bruders schwarz zu färben. Der Unterbaum hat nun in der Wurzel immer noch dieselbe Farbe wodurch die vierte Eigenschaft erhalten bleibt. Aber der Konfliktknoten hat nun einen weiteren schwarzen Vorfahren: Falls sein Vater vor der Transformation noch nicht schwarz war, so ist er nach der Transformation schwarz, und falls sein Vater schon schwarz war, so hat der Konfliktknoten nun seinen ehemaligen Bruder (S) als schwarzen Großvater, weswegen die Pfade welche durch den Konfliktknoten laufen nun einen zusätzlichen schwarzen Knoten passieren. Falls nun ein Pfad nicht durch den Konfliktknoten verläuft, so gibt es zwei Möglichkeiten: Der Pfad verläuft durch seinen neuen Bruder. Ist dies der Fall, so muss der Pfad sowohl vor als auch nach der Transformation durch den alten Bruder (S) und den neuen Vater des Konfliktknotens laufen. Da die beiden Knoten aber nur ihre Farben vertauscht haben ändert sich an der Schwarztiefe auf dem Pfad nichts. Der Pfad verläuft durch den neuen Onkel des Konfliktknotens welcher das rechte Kind des Bruders (S) ist. In diesem Fall ging der Pfad vorher sowohl durch seinen Bruder, dessen Vater, und das rechte Kind des Bruders(SR). Nach der Transformation geht er aber nur noch durch den Bruder (S) selbst – welcher nun die Farbe seines ehemaligen Vaters angenommen hat – und das rechte Kind des Bruders, das seine Farbe von Rot auf Schwarz geändert hat. Insgesamt betrachtet hat sich an der Schwarztiefe dieses Pfades also nichts geändert. In beiden Fällen verändert sich die Anzahl der schwarzen Knoten auf den Pfaden also nicht, wodurch die vierte Eigenschaft wiederhergestellt werden konnte. Anmerkung: Für den weißen Knoten im Bild ist es irrelevant ob er rot oder schwarz ist, solange seine Farbe sich während der Transformation nicht ändert.

 void delete_case6(node n) {
     sibling(n)->color = n->parent->color;
     n->parent->color = BLACK;
     if (n == n->parent->left) {
         /* Here, sibling(n)->color == BLACK && 
                  sibling(n)->right->color == RED */
         sibling(n)->right->color = BLACK;
         rotate_left(n->parent);
     }
     else
     {
         /* Here, sibling(n)->color == BLACK && 
                  sibling(n)->left->color == RED */
         sibling(n)->left->color = BLACK;
         rotate_right(n->parent);
     }
 }

Höhenbeweis

Wie schon in der Einleitung motiviert ist die besondere Eigenschaft von Rot-Schwarz-Bäumen, dass sie in logarithmischer Zeit – genauer in O(log₂ n) – ein Element im Baum suchen, löschen oder einfügen können. Diese Operationen sind auf allen binären Suchbäumen von der Höhe h des Baumes abhängig. Je niedriger nun die Höhe des Baumes ist, desto schneller laufen die Operationen. Kann man nun beweisen, dass ein binärer Suchbaum mit n Elementen nie eine gewisse Höhe (im Falle des Rot-Schwarz-Baumes 2 log₂(n+1)) überschreitet, so hat man bewiesen, dass die oben genannten Operationen im schlimmsten Fall logarithmische Kosten haben, nämlich die genannten Kosten von 2 log₂(n+1) für einen Baum in dem n Elemente gespeichert sind. Somit muss gezeigt werden, dass folgende Aussage gilt:

Für die Höhe h eines Ein Rot-Schwarz-Baumes, der n Schlüssel speichert, gilt: h ≤ 2 log₂(n+1)

Beweisidee

Zum Beweis dieser Eigenschaft muss man zuerst einen Hilfssatz über die Anzahl der inneren Knoten im Baum beweisen, und verbindet diese später mit der vierten Eigenschaft von Rot-Schwarz-Bäumen (es folgen nie zwei rote Knoten aufeinander) um die oben genannte Eigenschaft zu beweisen.

Hilfssatz

Jeder Unterbaum von x enthält mindestens 2^S(x) − 1 innere Knoten

Beweis des Hilfssatzes

Den Beweis hierzu führt man durch vollständige Induktion über die Schwarzhöhe S eines Knotens x.

Induktionsanfang (S = 0)

Falls S = 0, so handelt es sich um einen NIL-Knoten, der somit keine Kinder hat. Insbesondere ist die Anzahl der inneren Knoten dieses Baumes 0.

Somit gilt: 2⁰ − 1 = 1 − 1 = 0

Induktionsschritt (S > 0)

Geht man davon aus, dass der betrachtete Knoten x ein innerer Knoten sein muss, so hat dieser genau zwei Kinder (x₁ und x₂). Falls x die Schwarzhöhe S hat, so hat jedes seiner Kinder eine Schwarzhöhe von entweder S oder S-1, je nach dem ob das Kind rot oder schwarz ist. Da die Schwarzhöhe der Kinder nun jedoch kleiner oder gleich der Schwarzhöhe des Vaterknotens x ist, kann man an dieser Stelle die Induktionsannahme verwenden, welche garantiert, dass jedes der Kinder wieder 2^{S(x) − 1} − 1 innere Knoten hat. Somit folgt für die Anzahl der inneren Knoten in dem Unterbaum, zu dem x die Wurzel bildet, dass diese größer oder gleich (2^{S(x) − 1} − 1) + (2^{S(x) − 1} − 1) + 1 = 2^S(x) − 1 ist. Somit folgt die Behauptung.

Beweis

Betrachtet man nun noch die vierte Eigenschaft von Rot-Schwarz-Bäumen, so sieht man dass auf einem Pfad von der Wurzel zu einem Blatt mindestens die Hälfte der Knoten schwarz sein müssen. Somit muss die Schwarzhöhe der Wurzel selbst mindestens ½h sein. Nach dem eben bewiesenen Hilfssatz muss nun für die Anzahl der Knoten n im Baum gelten: $n \geq 2^{\frac{h}{2}} - 1$

Bringt man nun noch die 1 auf die linke Seite und logarithmiert, so folgt:

$\begin{matrix} & n & \geq & 2^{\frac{h}{2}} - 1 \\ \Leftrightarrow & n + 1 & \geq & 2^{\frac{h}{2}} \\ \Leftrightarrow & \log_2(n+1) & \geq & \frac{h}{2} \\ \Leftrightarrow & 2 \log_2(n+1) & \geq & h \\ \Leftrightarrow & h & \leq & 2 \log_2(n+1) \end{matrix}$

Somit folgt die Behauptung, dass ein Rot-Schwarz-Baum eine maximale Höhe h von 2log₂(n + 1) hat, und damit die Operationen suchen, einfügen und löschen in logarithmischer Zeit erledigen kann. Drückt man dieses Ergebnis in der O-Notation aus, so ergibt sich für die Kosten der oben genannten Operationen, dass sie alle in O(log₂ n) liegen.

Siehe auch

• 2-3-4-Baum
• AVL-Baum
• B-Baum
• Heap (Datenstruktur)
• Suchbaum

Literatur

1. ↑ Rudolf Bayer: Symmetric Binary B-Trees. Data Structure and Maintenance Algorithms. In: Acta Informatica. 1, 1972, S. 290-306. doi:10.1007/BF00289509.
2. ↑ Leo J. Guibas: A Dichromatic Framework for Balanced Trees. In: Proceedings of the 19th Annual Symposium on Foundations of Computer Science. 1978, S. 8-21.

• Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein: Introduction to Algorithms. 2. Auflage. MIT Press, Cambridge (Massachusetts) 2001, ISBN 0-262-03293-7. 
• Andrew Binstock, Jon Rex: Practical Algorithms for Programmers. Addison-Wesley Professional, 1995, ISBN 0-201-63208-X

Weblinks

• Java-Applet zur Arbeitsweise eines Rot-Schwarz-Baumes
• Semesterarbeit zum Thema Rot-Schwarz-Bäume

Dieser Artikel wurde in die Liste der lesenswerten Artikel aufgenommen. Vorlage:Lesenswert/Wartung/ohne DatumVorlage:Lesenswert/Wartung/ohne Version