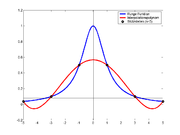
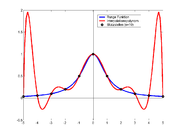
Runge-Funktion

Interpolation der Runge-Funktion (n=5)

Runges Phänomen (nach Carl Runge) ist ein Begriff aus der numerischen Mathematik und beschreibt eine Eigenschaft der Polynominterpolation, nach der eine Erhöhung des Grades des Interpolationspolynoms zu einer Verschlechterung der Interpolationsgüte führen kann.

Aufgabe der Polynominterpolation ist die Näherung einer Funktion durch eine Polynomfunktion. Bei ungünstiger Wahl der Stützstellen und hohem Grad des Polynoms kann es vorkommen, dass die Polynomfunktion kaum noch der zu interpolierenden Funktion ähnelt. Insbesondere bei äquidistanten Stützstellen "schwingt" die Polynomfunktion an den Intervallgrenzen. Daher sind Polynome höherer Ordnung (höher 5.–8. Ordnung) kaum für eine Interpolation mit geringem Fehler über das gesamte Intervall geeignet. Variabler Abstand der Stützstellen, die an den Intervallgrenzen dichter liegen vermindern zwar den Gesamtfehler der Interpolation, dennoch empfiehlt sich ein Wechsel des Interpolationsverfahrens zur Spline-Interpolation.

Interpolation der Runge-Funktion (n=10)

Runge gab für dieses Phänomen ein Beispiel an, die nach ihm benannte Runge-Funktion:

$f(x)=\frac{1}{1+(5x)^2}\,,\quad x\in[-5;5]$