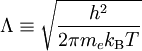Sahagleichung

Die Saha-Gleichung (auch Saha-Ionisierungs-Gleichung, Eggert-Saha-Gleichung oder Saha-Eggert-Gleichung) beschreibt im thermodynamischen Gleichgewicht die Abhängigkeit des Ionisierungsgrades eines Gases von der Temperatur. Sie wurde 1920 vom indischen Astrophysiker Meghnad Saha aus der Boltzmann-Statistik abgeleitet.

Für reine Gase lautet die Saha-Gleichung

$\frac{n_{i+1}\cdot{}n_e}{n_i} = \frac{2}{\Lambda^3}\frac{g_{i+1}}{g_i}\exp\left[-\frac{(\epsilon_{i+1}-\epsilon_i)}{k_{\rm B}T}\right]$

mit:

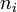• $n_i\,$ der Teilchendichte des ionisierten Gases (wobei i die Anzahl der fehlenden Elektronen ist)
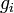• $g_i\,$ der Entartungsgrad des i-ten Energie-Niveaus
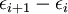• $\epsilon_{i+1}-\epsilon_i\,$ die Energiemenge, die benötigt wird, um ein weiteres Elektron aus einem Ion zu entfernen (von i zu i+1).
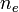• $n_e\,$ die Elektronendichte
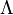• $\Lambda\,$ die De-Broglie-Wellenlänge (eines Elektrons)

$\Lambda \equiv \sqrt{\frac{h^2}{2\pi m_ek_{\rm B}T}}$

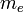• $m_e\,$ ist die Masse eines Elektrons (konstant)
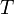• $T\,$ ist die Temperatur des Gases
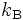• $k_{\rm B}\,$ ist die Boltzmannkonstante
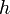• $h\,$ Plancksches Wirkungsquantum

Die Saha-Gleichung kann man so lesen, dass gerade diejenigen Atome ionisiert sind, bei denen die Energie der Elektronen gemäß der Boltzmann-Verteilung über der Ionisierungsenergie liegt.

Erreicht der Ionisierungsgrad eine nennenswerte Größenordnung, spricht man nicht mehr von einem Gas, sondern von einem Plasma. Die Eggert-Saha-Gleichung gilt für natürliche Plasmen, etwa in der Stratosphäre, im interplanetaren Raum oder innerhalb von Sternen. Für Laborplasmen ist sie nicht gültig, da sich diese nicht im thermischen Gleichgewicht befinden.