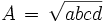Satz vom Tangentenviereck

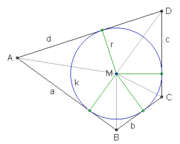
Ein Tangentenviereck ABCD mit Inkreis k

Ein Tangentenviereck ist ein Viereck, dessen Seiten Tangenten eines Kreises sind. Diesen Kreis nennt man den Inkreis des Tangentenvierecks.

Die (hier grün dargestellten) Senkrechten vom Inkreismittelpunkt (M) auf die vier Seiten zerlegen das Tangentenviereck in vier Drachenvierecke (mit grau gezeichneten Symmetrieachsen).

In einem Tangentenviereck ist die Summe zweier gegenüberliegender Seiten (z. B. a und c) gleich der Summe der anderen beiden Seiten (b und d). Es gilt also

a + c = b + d

Umgekehrt gilt auch, dass jedes Viereck mit dieser Eigenschaft (a + c = b + d) einen Inkreis besitzt und somit ein Tangentenviereck ist (Satz vom Tangentenviereck).

Der Mittelpunkt M des Inkreises befindet sich im Schnittpunkt der Winkelhalbierenden (hier grau gezeichnet) aller vier Eckwinkel (ABCD). Deshalb müssen sich beim Tangentenviereck alle Winkelhalbierenden auch in einem Punkt schneiden.

Formel zum Tangentenviereck
Flächeninhalt	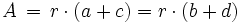$A \, = \, r \cdot (a+c) = r \cdot (b+d)$
Seitenlängen	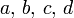$a,\,b,\,c,\,d$
Inkreisradius	$r\,$

Ein interessanter Spezialfall liegt vor, wenn ein Tangentenviereck die Bedingung

α + γ = β + δ

erfüllt. Unter dieser Voraussetzung ist das Tangentenviereck zugleich ein Sehnenviereck, also ein Viereck mit Umkreis; dieser stimmt natürlich nicht mit dem Inkreis überein. Die Flächenformel für Sehnenvierecke liefert in diesem Fall das einfache Ergebnis

$A \, = \, \sqrt{abcd}$

Spezielle Tangentenvierecke sind die Raute, das Quadrat und das Drachenviereck.

Konvexe Vierecke

Quadrat | Rechteck | Raute | Parallelogramm | Drachenviereck | Trapez | Sehnenviereck | Tangentenviereck