- Formelsammlung Geometrie
-
![\sqrt[n]{x}](4/5e4352778f3b156f05ef056f9793ec36.png)
Dieser Artikel ist eine Formelsammlung zum Thema Geometrie. Es werden mathematische Symbole verwendet, die im Artikel Mathematische Symbole erläutert werden. Die Formelsammlung zur euklidischen Geometrie ist ein Teil der Formelsammlung, in der auch Formeln der anderen Fachbereiche zu finden sind.
Inhaltsverzeichnis
Bezeichner und Schreibweisen
In den allermeisten Fällen gilt:
- Punkte werden mit lateinischen Großbuchstaben
 beschriftet.
beschriftet. - Linien wie Geraden, Strecken und Bögen werden mit lateinischen Kleinbuchstaben
 beschriftet.
beschriftet. - Winkel werden mit griechischen Kleinbuchstaben
 beschriftet.
beschriftet.
Im Folgenden werden Winkel im Gradmaß angegeben.
Geometrie in der Ebene
Grundlagen
Winkel
- Die Summe von Nebenwinkeln beträgt immer 180°.
α + β = 180°
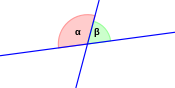
- Scheitelwinkel sind immer gleich groß.
α = β
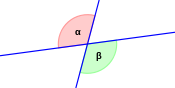
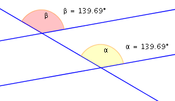
- Stufenwinkel an geschnittenen Parallelen sind immer gleich groß.
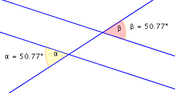
- Wechselwinkel an geschnittenen Parallelen sind immer gleich groß.
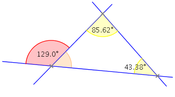
- Im Dreieck ist ein Außenwinkel gleich der Summe der beiden nichtanliegenden Innenwinkel.
- Die Summe der Innenwinkel in einem Dreieck ist immer 180°
- Die Summe der Innenwinkel in einem n-Eck ist immer

- Die Summe der Außenwinkel beträgt in einem konvexen n-Eck stets 360° (unabhängig von der Eckenzahl n)
Teilung einer Strecke
Verhältnisteilung: Um eine Strecke AB in einem bestimmten Verhältnis (in n gleiche Teile) zu teilen, zeichnet man zunächst einen beliebigen Strahl von A aus, der nicht parallel zu AB ist. Auf diesem trage man n mal eine beliebig lange Strecke ab. Den erhaltenen Endpunkt C verbinde man mit B und zeichne die Parallelen zu BC durch die bei der Unterteilung von AC entstandenen Punkte. Deren Schnittpunkte mit AB teilen AB in n gleiche Teile.
Flächen
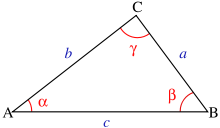
Die Standardbezeichnung für Dreiecke:
- Eckpunkte
- A,B und C. Beim gleichschenkligen Dreieck ist A die Ecke, an der die gleichen Seiten zusammenkommen und beim rechtwinkligen Dreieck ist C die Ecke mit dem rechten Winkel.
- Seiten
- a ist die der Ecke A gegenüberliegende Seite, entsprechendes gilt für b und c. Beim gleichseitigen Dreieck werden alle Seiten mit a bezeichnet.
- Winkel
- α ist der (Innen-)Winkel in Ecke A, β der Winkel in Ecke B und γ der Winkel in Ecke C.
Figur Flächeninhalt A Umfang U Bemerkung, Weiteres Dreieck Allgemeines Dreieck 


a + b + c Letztere Flächenformel wird als Satz des Heron bezeichnet.
k ist der halbe Umfang, R der Umkreisradius und r der Inkreisradius.Gleichseitiges Dreieck 

Alle Seiten sind gleich lang.
Alle Winkel sind gleich groß (60°).
Höhenlinien = Symmetrieachsen = Winkelhalbierende = Seitenhalbierende= MittennormaleGleichschenkliges Dreieck 
2a + c Zwei Seiten sind gleich lang (Schenkel a und b); die dritte Seite heißt Basis c
Die beiden Basiswinkel (α und β) sind gleich groß.
Die Höhenlinie durch C halbiert den Winkel γ
und die Basis c.Rechtwinkliges Dreieck 
a + b + c  .
.
Hypotenuse = längste Seite = Seite gegenüber dem 90°-Winkel.
Katheten = Seiten, die den rechten Winkel bilden.
Es gilt die Satzgruppe des Pythagoras (s.u.)Viereck Quadrat a2 
Diagonale 
Rechteck 

Diagonale 
Raute 

Parallelogramm 

ha ist die Höhe zur Seite a. Trapez 
a + b + c + d  = Mittellinie
= Mittelliniesymmetrischer Drachen 

Sehnenviereck 

a + b + c + d Viereck mit Umkreis, R Umkreisradius  ,
,
s halber Umfang; e,f Diagonalen: ,
,

Tangentenviereck 
a + b + c + d Viereck mit Inkreis mit Inkreisradius r.
Es gilt a + c = b + dPolygone regelmäßige Vielecke 





- n – Anzahl der Ecken
- ru – Radius des Umkreises, d. h. Entfernung vom Mittelpunkt zu einer Ecke
- ri – Radius des Inkreises, d. h. Entfernung vom Mittelpunkt zu einer Seitenmitte
- lk – Kantenlänge einer Seite des Vielecks
Kreis Kreis
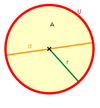


Es bezeichnet  die Kreiszahl.
die Kreiszahl.Kreisring 
R = Außenradius, r = Innenradius Kreisausschnitt
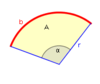



Länge des Kreisbogens b:

Kreisabschnitt (Segment)
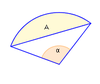

Kegelschnitte Ellipse πab


Menge der Punkte, für die die Summe der beiden Abstände zu zwei gegebenen Punkten (Brennpunkten) konstant (2a) ist. Der Umfang lässt sich nicht mit elementaren Funktionen angeben (→ Elliptisches Integral). D,d großer und kleiner Durchmesser. Kartesische Koordinaten: 
Hyperbel Keine geschlossene Fläche Keine geschlossene Kurve Menge aller Punkte, für die die absolute Differenz der Abstände zu den Brennpunkten konstant 2a ist. Kartesische Koordinaten: 
Parabel Keine geschlossene Fläche Keine geschlossene Kurve Menge aller Punkte, deren Abstand zu einem speziellen festen Punkt (dem Brennpunkt) und einer speziellen Geraden (der Leitgeraden l) konstant ist. Kartesische Koordinaten:  .
.Dreiecksgeometrie
Ausgezeichnete Punkte
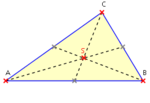
- Seitenhalbierende (Schwerlinien)
- teilen einander im Verhältnis 2:1.
- schneiden sich in einem Punkt, dem Schwerpunkt S des Dreiecks.
- teilen die Dreiecksfläche in je zwei gleich große Teilflächen.
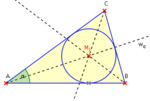
- Schnittpunkt der Mittelsenkrechten (Mittennormalen) = Mittelpunkt des Umkreises.
- Schnittpunkt der Winkelhalbierenden = Mittelpunkt des Inkreises.
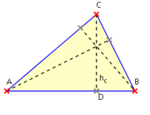
- Höhenlinien
- schneiden einander in einem Punkt H, dem Höhenschnittpunkt des Dreiecks.
- Die Höhe hc ist der Normalabstand des Punktes C zur Seite c (rechter Winkel bei D).
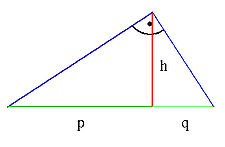
Satzgruppe des Pythagoras
- Satz des Pythagoras
- Im rechtwinkligen Dreieck ist die Fläche des Quadrats über der Hypotenuse gleich der Summe der Flächen der Quadrate über den Katheten:

- Kathetensatz
- Im rechtwinkligen Dreieck ist das Quadrat über einer Kathete flächengleich dem Rechteck aus der Hypotenuse und der Projektion dieser Kathete auf die Hypotenuse:

- Höhensatz
Dreiecksungleichung
Die Summe zweier Seiten eines Dreiecks ist stets größer als die dritte Seite.
Kongruenz- und Ähnlichkeitssätze
Zwei Dreiecke sind kongruent bzw. deckungsgleich, wenn sie übereinstimmen in
- drei Seiten z. B. a, b, c = n (sss)
- zwei Seiten und dem eingeschlossenen Winkel (sws)
- zwei Seiten und dem Gegenwinkel der längeren Seite (Ssw)
- einer Seite und den beiden anliegenden Winkeln (wsw)
Zwei Dreiecke sind ähnlich, wenn
- drei Paare entsprechender Seiten das gleiche Verhältnis haben
- zwei Paare entsprechender Seiten das gleiche Verhältnis haben und die von diesen Seiten eingeschlossenen Winkel übereinstimmen
- zwei Paare entsprechender Seiten dasselbe Verhältnis haben und die Gegenwinkel der längeren Seiten übereinstimmen
- zwei Winkel übereinstimmen
Strahlensätze
- Strahlensatz: Wird ein Zweistrahl durch zwei parallele Geraden geschnitten, so stehen die Strahlenabschnitte des ersten Strahles im gleichen Verhältnis wie die entsprechenden Abschnitte des zweiten Strahles.
- Strahlensatz: Wird ein Zweistrahl durch zwei parallele Geraden geschnitten, so stehen die Parallelabschnitte im gleichen Verhältnis, wie die vom Scheitelpunkt aus gemessenen zugehörigen Strahlenabschnitte.
Geometrie der Körper
Körper Volumen V Oberfläche O Bemerkungen, Weiteres Prismen Parallelepiped (Spat)
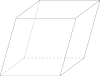


Quader
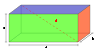


Raumdiagonalenlänge 
Allgemeines
Prisma

AM Mantelfläche Säulen Rundsäule (Zylinder) 

Hohlzylinder 


R,r Außen-,Innenradius
Maussen = 2πRh
Minnen = 2πrhPyramide Allgemeine
Pyramide

Pyramidenstumpf 

AG Grundfläche
AD DeckflächeKegel Kreiskegel 
nur für senkrechte Kegel:

Zusammenhang von Radius, Höhe und Seitenhöhe:

gerader Kegelstumpf 



r1,r2 RadienPlatonische Körper Tetraeder 

Hexaeder (Würfel) 

Raumdiagonalenlänge 
Oktaeder 

Dodekaeder 

Ikosaeder 

Kugel und Kugelteile Kugel 

Kugelkalotte (Kugelmütze, Kugelkappe) 
Kugelsegment (Kugelabschnitt) 

mit 
Kugelzone
(Kugelschicht)

mit  = Durchmesser des unteren Schnittkreises und
= Durchmesser des unteren Schnittkreises und  = Durchmesser des oberen Schnittkreises
= Durchmesser des oberen SchnittkreisesDrehkörper Ellipsoid 
Halbachsen a,b,c Torus 

siehe auch: Eulerscher Polyedersatz, Prinzip von Cavalieri
Trigonometrie
Analytische Geometrie
- Punkte werden mit lateinischen Großbuchstaben
Wikimedia Foundation.