Satz vom ausgeschlossenen Dritten (Philosophie)

Der Satz vom ausgeschlossenen Dritten (lat. tertium non datur, wörtlich: Ein Drittes ist nicht gegeben, engl. Law of the Excluded Middle) oder Prinzip des zwischen zwei kontradiktorischen Gegensätzen stehenden Mittleren (lat. principium exclusi tertii sive medii inter duo contradictoria) ist ein logisches Grundprinzip bzw. Axiom, das besagt, dass für eine beliebige Aussage mindestens die Aussage selbst oder ihr Gegenteil gelten muss; eine dritte Möglichkeit kann es nicht geben. Der Satz vom ausgeschlossenen Dritten ist zu unterscheiden vom Prinzip der Zweiwertigkeit, das aussagt, dass jede Aussage entweder wahr oder falsch ist. Er darf auch nicht verwechselt werden mit dem Satz vom Widerspruch, der besagt, dass die eine Aussage und ihr Gegenteil nicht gleichzeitig gelten können.

Logik

In der modernen formalen Logik bezieht sich der Satz vom ausgeschlossenen Dritten auf eine Aussage und deren Satzverneinung. Er besagt, dass für eine beliebige Aussage P die Aussage 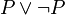$P\lor\neg P$ (P oder nicht P) gilt. Das bekannteste logische System, in dem der Satz vom ausgeschlossenen Dritten gilt, ist die klassische Logik.

Wenn z. B. P die Aussage

Hans ist blond.

bezeichnet, dann gilt inklusive Disjunktion

Hans ist blond oder es ist nicht der Fall, dass Hans blond ist.

Der Satz vom ausgeschlossenen Dritten sagt jedoch nichts darüber aus, ob P selbst gilt oder nicht.

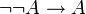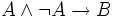Der Satz vom ausgeschlossenen Dritten ist nicht auf zweiwertige Logiken beschränkt, es gibt auch einige mehrwertige Logiken in denen er gilt. Umgekehrt gibt es jedoch auch zwei- und mehrwertige Logiken, in denen er nicht gilt. Einige Schlussregelkalküle, in denen er nicht gilt, ersetzen die Regel $\neg\neg A\to A$ durch $A\land\neg A\to B$ (siehe Wahrheitswert).

Interpretation

Interpretiert man den Satz vom ausgeschlossenen Dritten innerhalb der klassischen Logik (mit einer zweiwertigen Booleschen Algebra), dann ist er eine Tautologie, also unabhängig von der Wahl von P und unabhängig von dessen innerer Struktur wahr.

In logischen Systemen, in denen die atomaren Sätze und die Junktoren (Konnektive) anders interpretiert werden, ist dies nicht notwendigerweise der Fall. Zum Beispiel interpretiert die intuitionistische Logik die Aussage 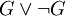$G\lor\neg G$ als die Existenz eines Beweises oder einer Widerlegung für die Aussage G. Da sehr viele konkrete Aussagen (z. B. die Kontinuumshypothese) weder beweisbar noch widerlegbar sind, gilt bei dieser Interpretation Tertium non datur nicht allgemein. Entsprechend sind Kalküle für solche logischen Systeme so konstruiert, dass der Satz 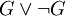$G\lor\neg G$ dort gilt.

Abgrenzung

Ob innerhalb eines bestimmten logischen Systems der Satz vom ausgeschlossenen Dritten gilt, kann rein formal untersucht werden. Daher sind diesbezüglich keine Meinungsverschiedenheiten möglich.

Von dieser rein logischen Fragestellung klar zu unterscheiden sind philosophische Fragestellungen, z. B. die metaphysische Frage, durch welche Art von logischem System (mit oder ohne Tertium non datur) sich die Wirklichkeit beschreiben lässt; oder die pragmatische Frage, mit welcher Art von logischem System sich etwa die Mathematik möglichst einfach vorantreiben lässt. Hinsichtlich dieser Fragen waren unter anderem im Grundlagenstreit rege Diskussionen im Gang.

Philosophie

Der Satz vom ausgeschlossenen Dritten hat eine lange philosophiegeschichtliche Tradition; in der traditionellen Logik gilt er als allgemein anerkanntes drittes Gesetz des Denkens und wird teils als ontologisches, teils als erkenntnistheoretisches Prinzip angesehen.

Als ontologisches Prinzip bedeutet er, dass es zwischen Sein und Nichtsein kein Drittes gibt^[1].

Den ersten gut bekannten Einwand gegen die Allgemeingültigkeit des Satzes vom ausgeschlossenen Dritten lieferte Aristoteles De interpretatione, Kapitel 7-9. Sein Argument ist, dass für Aussagen über die Zukunft wie den Satz „Morgen wird eine Seeschlacht stattfinden“ das Prinzip vom ausgeschlossenen Dritten nicht gelte, weil der Verlauf der Zukunft noch offen sei und eine Aussage über Zukünftiges daher weder wahr noch falsch sein könne.

Ablehnung

Wer den Satz (oder das Prinzip) vom ausgeschlossenen Dritten ablehnt oder kritisiert, behauptet nicht notwendig, dass es etwas Drittes gibt, sondern er lehnt logische Schlüsse ab, bei denen man aus der Logik und nicht aus den Tatsachen über den jeweiligen wissenschaftlichen Gegenstand etwas für wahr oder existent hält. Eine solche Kritik wurde zu Beginn des 20. Jahrhunderts sehr polemisch geäußert. Der Mathematiker, Logiker und Philosoph Luitzen Egbertus Jan Brouwer kritisierte besonders aus dem Satz vom ausgeschlossenen Dritten ableitbare Aussagen der Form:

Wenn für kein x gilt: nicht A(x), dann gilt für alle x: A(x)

Brouwer stellte intuitionistische Logikkalküle auf, in denen der Satz vom ausgeschlossenen Dritten nicht ableitbar ist. Relevant wird eine Ablehnung des Satzes bezüglich der Mathematik bei Aussagen über Unendliches und außerhalb der Mathematik bezüglich zukünftiger oder vergangener Ereignisse, wenn man von Wahrheit als gesichertem Wissen ausgeht (siehe auch Methodischer Konstruktivismus). Ein Beispiel ist die Behauptung: „Entweder war die Welt schon immer da oder sie hat irgendwann angefangen.“, die den Satz vom ausgeschlossenen Dritten braucht, um nach diesem Wahrheitsverständnis wahr zu sein.

Literatur

• Luitzen Egbertus Jan Brouwer: Begründung der Mengenlehre unabhängig vom logischen Satz vom ausgeschlossenen Dritten. Erster Teil, Allgemeine Mengenlehre. In Koninklijke Akademie van Wetenschappen te Amsterdam, Verhandelingen 1e sectie, deel XII, no 5 (1918), 1:43

Einzelnachweise

1. ↑ Vgl. Zoglauer, Thomas, Einführung in die formale Logik für Philosophen (1999), S.25