Satz von Shamir

In der theoretischen Informatik ist Vollständigkeit eine Eigenschaft von Problemen in Bezug auf eine Komplexitätsklasse. Intuitiv ist ein Problem dann vollständig für eine bestimmte Komplexitätsklasse, wenn kein anderes Problem der Klasse wesentlich schwieriger zu berechnen ist, und das Problem selbst ebenfalls in dieser Komplexitätsklasse enthalten ist. Ein vollständiges Problem einer Komplexitätsklasse beschreibt somit gewissermaßen die Schwierigkeit dieser Klasse.

Vollständige Probleme sind ein wichtiges Hilfsmittel zum Nachweis der Äquivalenz zweier auf unterschiedliche Weise definierten Komplexitätsklassen.

Von entscheidender Bedeutung für die formale Definition der Vollständigkeit ist das Konzept der Reduktion. Um einen sinnvollen Vollständigkeitsbegriff zu erhalten, muss die vorausgesetzte Reduktion weniger mächtig sein als die betrachtete Komplexitätsklasse.

Definition

Sei 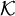$\mathcal{K}$ eine Komplexitätsklasse. Eine Sprache L ist genau dann 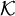$\mathcal{K}$-vollständig, wenn gilt:

• Jede Sprache 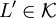$L^\prime\in\mathcal{K}$ ist auf L reduzierbar.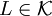
• $L\in\mathcal{K}$

In vielen Fällen wird hierbei eine logarithmisch platzbeschränkte Reduktion oder eine polynomiell zeitbeschränkte Reduktion angenommen. Es hängt von der Komplexitätsklasse ab, was hier sinnvoll ist.

Falls die erste, aber nicht notwendigerweise die zweite Bedingung erfüllt ist, so wird L als 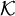$\mathcal{K}$-schwer oder 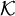$\mathcal{K}$-schwierig bezeichnet (manchmal auch als 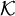$\mathcal{K}$-hart, in unglücklicher Übersetzung der englischen Bezeichnung 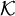$\mathcal{K}$-hard).

Äquivalenz von Komplexitätsklassen

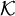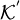Falls ein Problem vollständig für zwei verschiedene Komplexitätsklassen $\mathcal{K}$ und $\mathcal{K}^'$ ist, so gilt 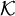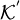$\mathcal{K}$=$\mathcal{K}^'$, sofern die beiden Klassen unter Reduktion abgeschlossen sind. Beispielsweise würde P = NP gelten, falls nachgewiesen werden könnte, dass P ein NP-vollständiges Problem enthält (siehe auch P-NP-Problem).

Ein Beispiel für die Anwendung dieses Prinzips ist der Satz von Shamir, durch den IP = PSPACE nachgewiesen wurde.

Vollständigkeitsnachweise

Falls noch kein vollständiges Problem für eine Klasse bekannt ist, muss zunächst eine generische Reduktion auf ein Problem dieser Klasse möglich sein. Durch eine generische Reduktion wird beispielsweise das zur Definition der Komplexitätsklasse verwendete Maschinenmodell durch dieses Problem ausgedrückt, wie etwa im Satz von Cook für die Klasse NP.

Nachdem hierdurch ein erstes vollständiges Problem der Komplexitätsklasse gefunden ist, wird der Vollständigkeitsnachweis für weitere Probleme meist einfacher. Um die Vollständigkeit eines Problems für eine bestimmte Komplexitätsklasse nachzuweisen, genügt es zu zeigen, dass ein bereits bekanntes vollständiges Problem dieser Klasse auf dieses Problem reduzierbar ist.

Notwendige Voraussetzung ist hierbei die Transitivität der betrachteten Reduktionsrelation.

Siehe auch

• NP-Vollständigkeit
• NP-Schwere

Quellen

• Christos H. Papadimitriou: Computational Complexity. Addison Wesley, ISBN 978-0201530827