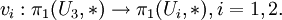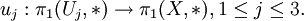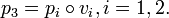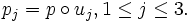Satz von Seifert-van Kampen

Der Satz von Seifert-van-Kampen (benannt nach Herbert Seifert und Egbert van Kampen) gehört zum Gebiet der algebraischen Topologie. Er macht eine Aussage über die Struktur der Fundamentalgruppe eines topologischen Raumes X, indem man die Fundamentalgruppen zweier offenen, wegzusammenhängenden Unterräume U und V welche X überdecken betrachtet. So kann man die Fundamentalgruppe von komplizierten Räumen aus denen einfacherer Räume berechnen.

Die einfache Hälfte von Seifert-van-Kampen

Es sei (X, * ) ein wegzusammenhängender punktierter Raum. Weiter sei 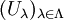$(U_{\lambda })_{\lambda \in \Lambda }$ eine offene Überdeckung von X durch wegzusammenhängende Teilmengen, die alle den Punkt * enthalten, und deren paarweise Schnitte jeweils auch wegzusammenhängend sind.

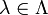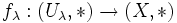Für $\lambda \in \Lambda$ sei $f_{\lambda }:(U_{\lambda },*) \rightarrow (X,*)$ die Inklusion. Dann wird π₁(X, * ) erzeugt von den Untergruppen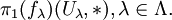 $\pi_{1}(f_{\lambda })(U_{\lambda },*),\lambda \in \Lambda.$

Die Aussage ist also, dass die relativen Homotopieklassen in X von geschlossenen Wegen, die ganz in einem U_λ verlaufen, die Fundamentalgruppe von X erzeugen. Insbesondere ist X einfach zusammenhängend, wenn jedes U_λ diese Eigenschaft besitzt.

Der eigentliche Satz von Seifert-van-Kampen

Es seien X ein wegzusammenhängender topologischer Raum, 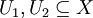$U_1 , U_2 \subseteq X$ offen und wegzusammenhängend, sodass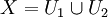$X = U_1 \cup U_2$ gilt, und 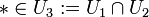$* \in U_3 := U_1 \cap U_2$ . Auch U₃ sei wegzusammenhängend. Zu den Inklusionen von U₃ nach U₁,U₂ gehören Homomorphismen

$v_i : \pi_1 (U_3 , *) \rightarrow \pi _1 (U_i , *), i = 1, 2.$

Zu den Inklusionen von U_j nach X gehören Homomorphismen

$u_j : \pi_1 (U_j , *) \rightarrow \pi_1 (X, *), 1 \leq j \leq 3.$

Offensichtlich gilt hierbei 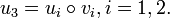$u_3 = u_i \circ v_i , i = 1, 2.$ Es seien weiter H eine beliebige Gruppe, und 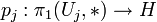$p_j : \pi_1 (U_j , *) \rightarrow H$ Gruppenhomomorphismen mit der Eigenschaft

$p_3 = p_i \circ v_i , i = 1, 2.$

Dann gibt es einen eindeutig bestimmten Gruppenhomomorphismus 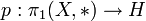$p : \pi_1 (X, *) \rightarrow H$, sodass

$p_j= p \circ u_j, 1 \leq j \leq 3.$

Also sagt der Satz von Seifert-van-Kampen eine universelle Abbildungseigenschaft der ersten Fundamentalgruppe aus.

Beispiel zum Hilfssatz

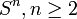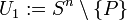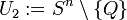Man nehme die n-dimensionale Sphäre $S^{n}, n \geq 2$ und Q,P zwei verschiedene Punkte aus Sⁿ. Dann sind $U_1 := S^n \setminus \{P\}$ und $U_2 := S^n \setminus \{Q\}$ wegzusammenhängend. Ihr Durchschnitt ist wegen 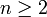$n \geq 2$ auch wegzusammenhängend.

Nun ist aber 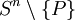$S^n \setminus \{P\}$, mittels der stereographischen Projektion, homöomorph zu $\mathbb{R}^n$. Da $\mathbb{R}^n$ kontrahierbar ist, gilt dies also auch für U₁ und U₂ und daher haben diese triviale Fundamentalgruppen. Dies ist nicht vom Fußpunkt abhängig. Daher ist auch π₁(Sⁿ) trivial.

Folgerungen

Wenn die Fundamentalgruppe π₁(U₃, * ) trivial ist, dann sagt der Satz von Seifert van Kampen, dass π₁(X, * ) das freie Produkt von π₁(U₁, * ) und π₁(U₂, * ) ist. Es wird von diesen Gruppen erzeugt und zwischen den Erzeugern gibt es keine Relationen, die nicht schon in π₁(U₁, * ) oder π₁(U₂, * ) gewesen wären. Insbesondere sind u₁ und u₂ injektiv.

Quellen

• Stefan Kühnlein, Skript: Einführung in die Topologie (2008)

Siehe auch

• Zum besseren Verständnis der Beweise bzw. der Verallgemeinerungen: Lebesguezahl, Gruppoid, Pushout, Freies Produkt, Amalgamiertes Produkt
• Sebastian Hage, Seminarvortrag: Der Satz von Seifert-van Kampen - Gruppoide, Pushouts & der Satz von Brown (2004). Enthält einen kategorientheoretischen sowie einen topologischer Beweis des Satzes.