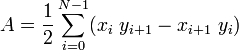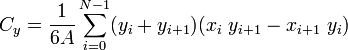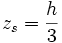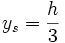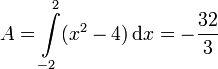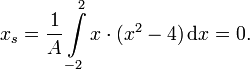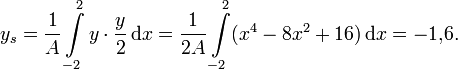Schwerachse

Der Schwerpunkt oder das Gravizentrum (engl. Center of Gravity, COG bzw. C/G) stellt das Zentrum, die gemittelte Position einer Ansammlung eines oder mehrerer Objekte, bezogen auf die Schwerkraft, dar. Im Schwerpunkt angreifende externe Kräfte können den Rotationszustand des Objekts nicht verändern.

Bei näherer Betrachtung weist der Begriff des Schwerpunkts eine komplexere Struktur auf als man von der intuitiven Anschauung her (unter vereinfachenden Bedingungen wie konstante Schwerkraft und homogene Dichte) erwartet. Der Gesamtschwerpunkt einer Ansammlung lässt sich oft ermitteln aus der gewichteten Summe der Schwerpunkte ihrer Subsysteme, die so gewählt werden, dass ihre Schwerpunkte leicht zu bestimmen sind. Falls das nicht geht (z. B. bei unregelmäßig geformten Körpern), wird er berechnet als das erste Moment der Verteilungsfunktion der Wichte dieser Ansammlung im Raum, normiert auf das Gesamtgewicht G:

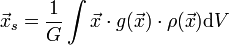$\vec x_s=\frac{1}{G}\int \vec x \cdot g(\vec x)\cdot \rho(\vec x)\mathrm dV$ mit $G=\int g(\vec x)\cdot \rho(\vec x)\mathrm dV.$

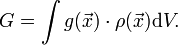
Die Verteilungsfunktion ist das Produkt einer externen und einer internen Komponente: die externe wird von der ortsabhängigen Schwerkraft 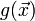$g(\vec x)$ gebildet, die interne von der Ansammlung definierte ist die Dichte 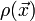$\rho(\vec x)$. Diese Dichte gibt an, wo wie viel von „dem, was dem betrachteten System zugeordnet wird,“ lokalisiert ist, außerhalb ist sie Null; so beschreibt die Dichtefunktion die Form der Objekte. Bei einem konstanten Schwerefeld (wie zum Beispiel näherungsweise auf der Erdoberfläche oder bei Objekten, die so klein sind, dass sich die Schwerkraft im Bereich ihres Volumens sich nicht merklich ändert) stimmt der Schwerpunkt des Systems mit seinem Massenmittelpunkt überein, der begrifflich zu den Erwartungswerten gehört, die aus der Statistik oder der Quantenmechanik bekannt sind, wobei die Dichtefunktion der Wahrscheinlichkeitsdichte bzw. dem Quadrat der Wellenfunktion entspricht.

Ist darüber hinaus auch die Dichte innerhalb bestimmter Teilbereiche des betrachteten Volumens konstant, fällt der Schwerpunkt (sowie der Massenmittelpunkt) dieses Teilbereichs mit dem rein geometrischen Volumenschwerpunkt zusammen und lässt sich häufig aus den geometrischen Symmetrien der Form des Objektes oder seiner Teile (Quader, Kugel, Zylinder etc) erschließen. Er muss beispielsweise auf den Symmetrieachsen im Zentrum der jeweiligen Form liegen und kennzeichnet näherungsweise ihre Lage im Raum durch einen (Mittel)Punkt. Sind die Teilmassen und die Positionen ihrer jeweiligen Schwerpunkte bereits bekannt, braucht man die Teilvolumina nicht zu berechnen und der Gesamtschwerpunkt wird gebildet als Summe der mit den Orten der jeweiligen Schwerpunkte gewichteten Teilmassen, normiert auf die Gesamtmasse.

Sind die Teilobjekte (Massen-, Volumen-, Flächen- oder Linienelemente) klein gegenüber dem Gesamtsystem, kann man für ihre Schwerpunkte einfach ihre Position verwenden. So ergibt sich der Volumenschwerpunkt einer geometrischen Figur (egal ob massiv oder nicht) im Allgemeinen als ortsgewichtete normierte Summe der Volumenelemente. Entsprechend berechnet man den geometrischen Flächen- oder Linienschwerpunkt als ortsgewichtete normierte Summe der zum System gehörenden Flächen- oder Linienelemente.

Physikalischer Schwerpunkt

Im Sinne der klassischen Mechanik ist der Schwerpunkt der Punkt, an dem die Masse des Körpers die gleiche Wirkung auf andere Körper hätte, wenn sie in diesem Punkt vereint wäre. Umgekehrt kann man die Gravitation, die auf alle Massenpunkte des Körpers wirkt, durch eine einzige Kraft darstellen, die im Schwerpunkt angreift.

Wenn ein Körper weit genug von anderen Körpern entfernt ist bzw. wenn er sehr klein ist im Vergleich zum anziehenden Körper, dann kann man den Körper als einen Massenpunkt annähern, dessen Masse im Schwerpunkt vereinigt ist. Das gilt zum Beispiel für einzelne Planeten im Weltraum oder für Gegenstände auf der Erdoberfläche. Wenn sich die Stärke des Gravitationsfeldes nur wenig ändert, so dass sie über der ganzen Ausdehnung des Körpers als konstant angenommen werden kann, dann fällt der Schwerpunkt nahezu mit dem Massenmittelpunkt zusammen. Das gilt zum Beispiel für Körper auf der Erdoberfläche oder Satelliten in einer Umlaufbahn, nicht aber für den Mond oder auch die Erde in Bezug auf das Gravitationsfeld des Mondes. In der Nähe eines Schwarzen Loches würde selbst für einen kleinen Körper wie ein Raumschiff oder sogar einen Menschen das Gravitationsfeld für verschiedene Teile des Körpers merklich verschieden sein. In einem solchen Fall treten Gezeitenkräfte auf.

Ist ein Körper homogen, besteht er also aus einem Material, das überall die gleiche Dichte hat, so entspricht sein Massenmittelpunkt und damit näherungsweise auch sein Schwerpunkt dem geometrischen Volumenschwerpunkt, der weiter unten erklärt wird. Besteht der Körper aus Teilen verschiedener Dichte, kann der Massenmittelpunkt vom Volumenschwerpunkt abweichen. Wenn die Verteilung der Dichte innerhalb des Körpers bekannt ist, kann der Massenmittelpunkt durch Integration berechnet werden. Dies war der Anlass, aus dem Isaac Newton die Infinitesimalrechnung entwickelte (gleichzeitig mit Leibniz).

Der Trägheitsschwerpunkt eines Körpers, also der Mittelpunkt bezüglich des Trägheitsmoments, fällt mit seinem Massenmittelpunkt zusammen. Er kann also bei einem ausgedehnten Körper bzw. in einem sich über kurze Entfernungen ändernden Gravitationsfeld vom Schwerpunkt abweichen. Liegt beispielsweise ein (homogener) Ziegelstein auf einem Tisch, so ist dessen untere Hälfte etwas dichter am Erdmittelpunkt als die obere Hälfte, weshalb die unterschiedlich starke Gravitation dazu führt, dass der (Gravitations-)Schwerpunkt ein wenig näher am Erdmittelpunkt („unten“) liegt als der Massenmittelpunkt bzw. Trägheitsschwerpunkt.

In der Himmelsmechanik bezeichnet man den Massenschwerpunkt eines Systems von mehreren Himmelskörpern als Baryzentrum. Im Schwerpunktsystem wird der Schwerpunkt als Koordinatenursprung verwendet. Siehe auch: Mehrkörper-System

Bei alldem muss man sich darüber im Klaren sein, dass der Schwerpunkt eines Körpers nicht unbedingt im Inneren des Körpers liegen muss. Das gilt natürlich für Körper mit Hohlräumen, kann aber auch ganz allgemein für beliebige nichtkonvexe Körper gelten. Beispiele dafür sind der Torus, ein mondsichelförmiger Bogen oder so triviale Alltagsgegenstände wie eine Tasse oder eine Schale.

Bestimmung des Schwerpunktes

Der Schwerpunkt liegt unter dem Aufhängepunkt auf der „Schwerlinie“.

Bestimmung des Schwerpunkts als Schnittpunkt der „Schwerlinien“.

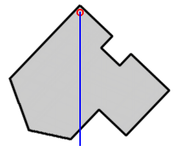
Aus den obigen Ausführungen gelangt man zu einem einfachen Verfahren zur annähernden Bestimmung des Schwerpunktes eines beliebigen starren Körpers, wobei die Näherung darin besteht, die Abweichungen von Schwerpunkt und Massenmittelpunkt und damit auch die Veränderungen der Lage des Schwerpunktes bei Drehung des Körpers (verbunden mit Gravitationskraftänderungen in den einzelnen Körperregionen) unberücksichtigt zu lassen: Hängt man den Körper an einem beliebigen Punkt auf, so liegt (in Ruhe) der (näherungsweise) Schwerpunkt auf der lotrechten Linie (= „Schwerlinie“) durch den Aufhängepunkt (blaue Linie im Bild rechts).

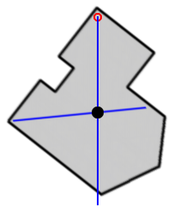
Wiederholt man dies mit einem anderen Aufhängepunkt, so findet man den (näherungsweisen) Schwerpunkt als Schnittpunkt zweier solcher Geraden („Schwerlinien“). Dass ein solcher Schnittpunkt tatsächlich existiert und unabhängig von der Wahl der Aufhängepunkte ist, ist allerdings weniger trivial, als der erste Anschein glauben lässt.

Verblüffend ist die folgende Methode, um den Schwerpunkt eines schmalen und länglichen Gegenstandes (z. B. Lineal oder Besen) zu bestimmen: Man lege den Gegenstand quer über die beiden auf gleicher Höhe nach vorne ausgestreckten Zeigefinger, was leicht möglich ist, solange die Finger noch weit von einander entfernt sind. Nun bringe man langsam die Zeigefinger näher zueinander, bis sie sich berühren, wobei man sie stets auf möglichst gleicher Höhe hält. Sofern man dies langsam genug macht, gleitet der Gegenstand langsam über die Finger, ohne nach einer Seite zu kippen. Auf den Finger, der dem Schwerpunkt näher liegt, lastet jeweils ein stärkerer Druck, was zu einer stärkeren Reibung führt, d. h. der Gegenstand gleitet vornehmlich über den anderen Finger. Hierdurch regelt sich das System so ein, dass bei beiden Fingern in etwa dieselbe Reibung vorliegt und der Schwerpunkt sich in ihrer Mitte befindet. Schließlich berühren sich also die Zeigefinger, der Gegenstand liegt nach wie vor waagerecht und der Schwerpunkt liegt über den beiden Fingern. (Ist der Gegenstand allerdings zu sehr gebogen, ergibt sich der oben erwähnte Effekt und der Schwerpunkt liegt unterhalb des Unterstützungspunktes.)

Geometrischer Schwerpunkt

Den Schwerpunkt einer Fläche oder eines Körpers kann man mit Mitteln der Mathematik, der Geometrie, berechnen, oder, wenn die Fläche bzw. der Körper aus homogenem Material hergestellt wird, rein mechanisch durch Balancieren bestimmen. Letztere Methode wird oft (an Modellen) angewandt, wenn es um geografische Mittelpunkte von Kontinenten oder Ländern geht (z. B. Mittelpunkt Europas, Mittelpunkt Deutschlands).

Beispiele geometrischer Flächen

Ebene Flächen

Bei ebenen Flächen lässt sich der Schwerpunkt allgemein dadurch ermitteln, dass man die ausgeschnittene Fläche an einem Punkt aufhängt und die Lotgerade, eine so genannte Schwerelinie einzeichnet. Der Schnittpunkt zweier Schwerelinien ist der Schwerpunkt. Alle weiteren Schwerelinien schneiden sich ebenfalls in diesem Schwerpunkt.

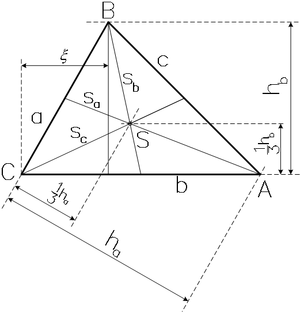
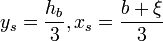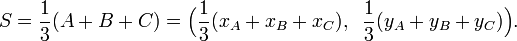
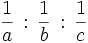
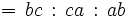
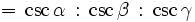
Dreieck	$y_s=\frac{h_b}{3},x_s=\frac{b+\xi}{3}$, Der Schwerpunkt S eines Dreiecks liegt im Schnittpunkt der Seitenhalbierenden. Man nennt sie daher auch Schwerelinien. Im Allgemeinen berechnet sich der Schwerpunkt in kartesischen Koordinaten: $S = \frac13(A+B+C) = \Big(\frac13 (x_A+x_B+x_C),\;\; \frac13(y_A+y_B+y_C)\Big).$ Ausgedrückt durch Trilineare Koordinaten: $\frac{1}{a} \, : \, \frac{1}{b} \, : \, \frac{1}{c}$ $= \, bc \, : \, ca \, : \, ab$ $= \, \csc\alpha \, : \, \csc\beta \, : \, \csc\gamma$ Ausgedrückt durch Baryzentrische Koordinaten: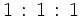$1 \, : \, 1 \, : \, 1$
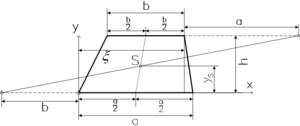
Trapez	Der Schwerpunkt des Trapezes lässt sich folgendermaßen konstruieren: Eine Schwerelinie halbiert die beiden parallelen Seiten. Eine zweite erhält man, indem man die parallelen Seiten um die Länge der jeweils anderen in entgegengesetzten Richtungen verlängert, und die beiden Endpunkte miteinander verbindet. Die Formel in kartesischen Koordinaten lautet (gemessen vom linken unteren Eckpunkt): $y_s=\frac{h}{3}\cdot \frac{a+2b}{a+b}, x_s=\frac{a^2-b^2+\xi(a+2b)}{3(a+b)}$
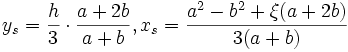
Polygon	Der Schwerpunkt eines nicht überschlagenen, geschlossenen Polygons mit N Eckpunkten kann wie folgt berechnet werden[1] (der nullte Eckpunkt (x0 , y0) und der N-te Eckpunkt (xN , yN) sind hierbei identisch): Die Fläche des Polygons ist: $A = \frac{1}{2}\sum_{i=0}^{N-1} (x_i\ y_{i+1} - x_{i+1}\ y_i)$ Der Flächenschwerpunkt des Polygons ist: $C_x = \frac{1}{6A}\sum_{i=0}^{N-1}(x_i+x_{i+1})(x_i\ y_{i+1} - x_{i+1}\ y_i)$ $C_y = \frac{1}{6A}\sum_{i=0}^{N-1}(y_i+y_{i+1})(x_i\ y_{i+1} - x_{i+1}\ y_i)$
Halbkreisfläche	$y_s=\frac{4r}{3\pi}$

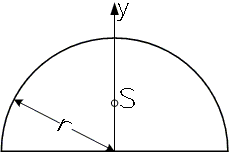
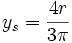
Räumliche (gekrümmte) Begrenzungsflächen

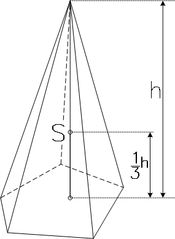
• Pyramide und Kegel:

Flächenschwerpunkt (Hohlkörper): $z_s=\frac{h}{3}$

Volumenschwerpunkt (Vollkörper): $z_s=\frac{h}{4}$

• Volumenschwerpunkt eines massiven Rotationsparaboloids: $y_s=\frac{h}{3}$

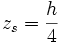
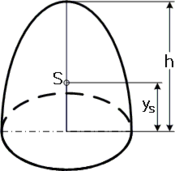
der Flächenschwerpunkt eines Rotationsparaboloids (umgestülptes Sektglas) liegt zwischen 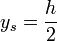$y_s=\frac{h}{2}$ (h klein) und 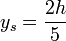$y_s=\frac{2h}{5}$ (h groß).

• Kugelsegment (Orientierung wie Paraboloid, $\quad h\le2r)$:

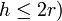Der Volumenschwerpunkt (Vollkörper) beläuft sich auf: $y_s=\frac{4r-h}{4(3r-h)}\cdot h,$

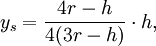
der Flächenschwerpunkt (Schale) beträgt: $y_s=\frac{h}{2} .$

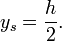
Schwerpunkt einer Linie

beliebiger flacher Bogen:	$z_s\approx\frac{2h}3$
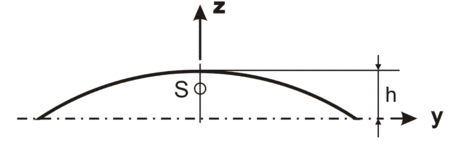
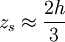
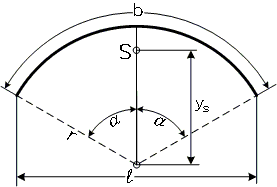
Kreisbogen:	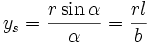$y_s=\frac{r\sin\alpha}\alpha=\frac{rl}b$ (mit α in Bogenmaß) 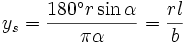$y_s=\frac{180^\circ r\sin\alpha}{\pi\alpha}=\frac{rl}b$(mit α als Winkelmaß)

Siehe auch: Rotationsfläche, Rotationskörper

Zusammenfassen von Schwerpunkten

Es ist möglich, mehrere Schwerpunkte einzelner einfacher Elemente zu einem gemeinsamen Schwerpunkt zusammenzufassen.

1-dimensional	2-dimensional	3-dimensional	allgemein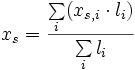
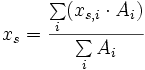
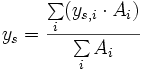
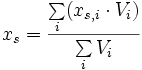
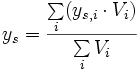
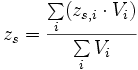
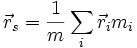
$x_s=\frac{\sum\limits_i (x_{s,i} \cdot l_i)}{\sum\limits_i l_i}$	$x_s=\frac{\sum\limits_i (x_{s,i} \cdot A_i)}{\sum\limits_i A_i}$ $y_s=\frac{\sum\limits_i (y_{s,i} \cdot A_i)}{\sum\limits_i A_i}$	$x_s=\frac{\sum\limits_i (x_{s,i} \cdot V_i)}{\sum\limits_i V_i}$ $y_s=\frac{\sum\limits_i (y_{s,i} \cdot V_i)}{\sum\limits_i V_i}$ $z_s=\frac{\sum\limits_i (z_{s,i} \cdot V_i)}{\sum\limits_i V_i}$	$\vec{r}_s=\frac{1}{m}\sum\limits_i \vec{r}_i m_i$

Der Abstand x_s (bzw. y_s, z_s) ist jener von einem frei wählbaren Koordinatenursprung. Weist eine Fläche (ein Körper) Aussparungen auf, so können obige Summenformeln ebenfalls angewendet werden, jedoch muss beachtet werden, dass die ausgesparten Flächen (Volumen) mit negativem Vorzeichen in die Berechnung mit eingehen.

Schwerpunkt von Flächen und Körpern, deren Begrenzung durch den Graphen einer Funktion gegeben ist

In den vorherigen Abschnitten wurden ausschließlich Flächen und Körper behandelt, deren Gestalt bestimmten geometrischen Grundformen entspricht. Wenn dieser Sachverhalt nicht gegeben ist und die Begrenzung von Körpern bzw. Flächen durch Graphen von Funktionen gegeben sind, so kommt zur Berechnung der Schwerpunktskoordinaten die Integralrechnung zur Anwendung.

Dann gilt:

2-dimensional	3-dimensional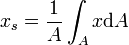
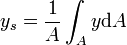
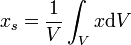
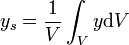
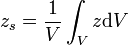
$x_s=\frac{1}{A}\int_A x \mathrm dA$ $y_s=\frac{1}{A}\int_A y \mathrm dA$	$x_s=\frac{1}{V}\int_V x \mathrm dV$ $y_s=\frac{1}{V}\int_V y \mathrm dV$ $z_s=\frac{1}{V}\int_V z \mathrm dV$

Zur praktischen Bestimmung der x-Koordinate des Schwerpunktes im 2-dimensionalen Fall substituiert man dA mit 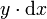$y\cdot \mathrm dx$, was einem infinitesimalen Flächenstreifen entspricht. Ferner entspricht hierbei y der die Fläche begrenzende Funktion y(x).

Für die praktische Berechnung der y-Koordinate im 2-dimensionalen Fall gibt es prinzipiell zwei Vorgehensweisen:

• entweder man bildet Umkehrfunktion x(y) und berechnet das Integral 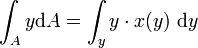$\int_A y \mathrm dA = \int_y y\cdot x(y) \ \mathrm dy$ , wobei die „neuen“ Integrationsgrenzen nun auf der y-Achse zu finden sind.
• oder man nutzt aus, dass der Schwerpunkt eines jeden zur y-Achse parallelen infinitesimalen Flächenstreifen 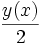$\frac{y(x)}{2}$ ist. Dann erhält man zur Bestimmung der y-Koordinate eine einfachere Formel, mit deren Hilfe das Bilden der Umkehrfunktion erspart bleibt:

$y_s=\frac{1}{A}\int_A y \mathrm dA = \frac{1}{A}\int_x y\cdot\frac{y}{2}\ \mathrm dx$

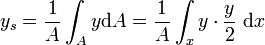
Beispiel: Schwerpunkt einer Parabel

Wir suchen den Flächenschwerpunkt jener Fläche, die durch eine Parabel y₁ = x² − 4 und durch die x-Achse definiert ist.

Zuerst bestimmen wir den Inhalt A der Fläche

$A = \int\limits_{-2}^2 (x^2-4)\,\mathrm dx = -\frac{32}3$

Die Grenzen des Integrals sind bei Begrenzung der Fläche durch die x-Achse die Nullstellen der Funktion.

Die x-Koordinate des Schwerpunktes ergibt sich zu

$x_s = \frac 1A\int\limits_{-2}^2 x\cdot (x^2-4)\,\mathrm dx = 0.$

Die y-Koordinate ergibt sich zu

$y_s = \frac 1A\int\limits_{-2}^2 y\cdot\frac y2\,\mathrm dx= \frac 1{2A}\int\limits_{-2}^2 (x^4-8x^2+16)\,\mathrm dx= -1{,}6.$

Einzelnachweise

1. ↑ Calculating the area and centroid of a polygon

Weblinks

• Herleitung von Formeln zum Schwerpunkt