- Flächenträgheitsmoment
-
Das Flächenträgheitsmoment, auch als Flächenmoment 2. Grades bezeichnet, ist in der technischen Mechanik eine aus dem Querschnitt eines Balkens abgeleitete geometrische Größe, die an der Beschreibung seines Widerstands gegen Beanspruchung auf Biegung und Torsion beteiligt ist. Diese ist auch an der Beschreibung der Stabilität von Stäben gegen Knicken und von Schalen gegen Beulen beteiligt.
Flächenträgheitsmomente werden benötigt, um bei der Dimensionierung von Bauteilen deren elastische Verformung und vor allem deren Belastbarkeit zu bestimmen, bevor bleibende Verformung, Bruch, Knicken oder Beulen eintreten.
Der Widerstand gegen elastische Verformung bei Biegung und Torsion und die Stabilitätsgrenze vor Knicken oder Beulen sind auch von der Elastizität des verwendeten Werkstoffs, der Widerstand gegen Versagen (bleibende Verformung, Bruch) außerdem von der Werkstoff-Festigkeit abhängig.
Inhaltsverzeichnis
Arten
 symmetrische und unsymmetrische Querschnitte eines Balkens, der beispielsweise einseitig eingespannt (1 und 2, Kragträger) auf Biegung und Torsion (4) beansprucht wird.
symmetrische und unsymmetrische Querschnitte eines Balkens, der beispielsweise einseitig eingespannt (1 und 2, Kragträger) auf Biegung und Torsion (4) beansprucht wird.
Grundsätzlich gibt es drei Arten Flächenträgheitsmomente:
axiales Flächenträgheitsmoment
Das axiale Flächenträgheitsmoment ist ein Maß für den Widerstand eines Balkens gegen Biegung. Die Erfahrung zeigt, dass ein vertikal belasteter Balken sich weniger durchbiegt, wenn er hochkant (1 im Bild) und nicht flach (2 im Bild) liegt. Das axiale Flächenträgheitsmoment berücksichtigt das, indem die vertikale Dimension mit höherer Potenz als die horizontale bewertet wird (dritte Potenz beim Flächenträgheitsmoment, zweite Potenz beim Widerstandsmoment).
polares Flächenträgheitsmoment
Das polare Flächenträgheitsmoment ist die Summe aus den axialen Flächenträgheitsmomenten in zwei senkrecht zueinander stehenden Richtungen. Es ist ein Maß für den Widerstand von Kreisquerschnitten und geschlossenen Kreisringquerschnitten gegen Torsion - siehe Balken (4) im Bild. Für alle anderen Fälle ist ein Torsionsträgheitsmoment definiert, für das sich nur in besonderen Fällen eine geschlossene Formel angeben lässt. Betrachtet werde ein einseitig eingespanntes Rohr, das an seinem äußeren Ende mit einem Drehmoment belastet (tordiert) wird: Die Erfahrung zeigt, dass ein Rohr sich dabei um so weniger verdreht, je größer sein Durchmesser ist. Das polare Flächenträgheitsmoment berücksichtigt das, indem der Durchmesser mit höherer Potenz bewertet wird (vierte Potenz beim Flächenträgheitsmoment, dritte Potenz beim Widerstandsmoment).
biaxiales Flächenträgheitsmoment
Das biaxiale Flächenträgheitsmoment, auch als Flächendeviationsmoment, Deviationsmoment, Flächenzentrifugalmoment oder Zentrifugalmoment bezeichnet, ist von Bedeutung bei der Bestimmung der Deformation von unsymmetrischen Profilen und / oder bei unsymmetrischer Belastung beliebiger Profile - siehe Balken (3) im Bild.
Berechnung
Einheiten
Die Flächenträgheitsmomente werden üblicherweise in m4 angegeben (SI-Einheiten). Im veralteten, in den USA aber noch gebräuchlichen Einheitensystem werden sie normalerweise in in4 notiert.
axiales Flächenträgheitsmoment
Die axialen Flächenträgheitsmomente lassen sich durch diese Gleichungen beschreiben:
 , [I] = m4
, [I] = m4
- z = senkrechter Abstand der y-Achse zum Element dA
 , [I] = m4
, [I] = m4
Beide Größen können nur positive Werte annehmen.
polares Flächenträgheitsmoment
Das polare Flächenträgheitsmoment setzt sich aus den beiden Flächenträgheitsmomenten Iy und Iz zusammen:
 , [I] = m4
, [I] = m4
biaxiales Flächenträgheitsmoment
Das biaxiale Flächenträgheitsmoment wird durch diese Gleichung beschrieben:
 , [I] = m4
, [I] = m4
Diese auch Deviations- oder Zentrifugalmoment genannte Größe ist gleich Null, wenn entweder die y-Achse oder die z-Achse eine Symmetrieachse des Querschnitts ist. Die zugehörigen Flächenträgheitsmomente heißen dann Hauptträgheitsmomente, sie nehmen in diesem Falle extremale Werte an. Im Gegensatz zu den axialen und zum polaren Flächenträgheitsmoment kann diese Größe sowohl positive als auch negative Werte annehmen. Neben dieser Definition mit negativem Vorzeichen wird je nach Literatur auch eine Definition mit positivem Vorzeichen verwendet, dies ist in allen Formeln die das Deviationsmoment verwenden zu berücksichtigen.
Satz von Steiner
Alle hier genannten Flächenträgheitsmomente werden auf einen speziellen Punkt, nämlich den Flächenschwerpunkt bezogen. Für alle anderen Punkte können die Flächenträgheitsmomente mit dem Steinerschen Satz berechnet werden.
Der Satz von Steiner besagt, dass sich das Flächenträgheitsmoment einer beliebigen Querschnittsfläche zusammensetzt aus den Flächenträgheitsmomenten im Hauptachsensystem der einzelnen Teilflächen und dem Produkt aus dem Quadrat des Abstandes z von Schwerachse-Gesamtfläche zu Schwerachse-Teilfläche und Teilfläche A. Ein Anwendungsbeispiel ist die I-Form. Die Flächenträgheitsmomente der drei rechteckigen Teilflächen, nämlich der beiden horizontalen Flansche und des vertikalen Stegs, lassen sich über die unten angegebenen Formeln bestimmen und für die vertikale z-Achse zu
 einfach summieren, denn alle Schwerpunkte der Teilflächen liegen auf der gemeinsamen Schwerachse z der Gesamtfläche. Das Flächenträgheitsmoment
einfach summieren, denn alle Schwerpunkte der Teilflächen liegen auf der gemeinsamen Schwerachse z der Gesamtfläche. Das Flächenträgheitsmoment  bezüglich der y-Achse setzt sich ebenfalls aus den drei Summanden plus dem Steiner'schen Anteil der beiden Flansche zusammen.
bezüglich der y-Achse setzt sich ebenfalls aus den drei Summanden plus dem Steiner'schen Anteil der beiden Flansche zusammen.Hauptträgheitsmomente und verdrehte Trägheitsmomente
 ,
, ,
, ,
, ,
,
Mit Hilfe dieser Formeln kann man die zugehörigen Trägheitsmomente einer Fläche berechnen, wenn die Koordinatenachsen der Fläche um einen beliebigen Winkel φ verdreht werden. Neben dem Winkel müssen auch die Hauptträgheitsmomente Iyy und Izz gegeben sein. Da in früheren Jahren noch keine zuverlässigen Rechenmaschinen zur Verfügung standen, wurde ein grafisches Verfahren von Christian Otto Mohr angegeben. Der Mohrsche Trägheitskreis ist noch in vielen Lehrbüchern über die Technische Mechanik zu finden. Eine praktische Anwendung finden die verdrehten Flächenträgheitsmomente bei der Berechnung von Spannungen, wenn bei der Biegung das belastende Biegemoment nicht in die Richtung eines der beiden Hauptträgheitsmomente fällt.
Abgeleitete Größen
Widerstandsmoment
Das Widerstandsmoment ist nötig, um die am Querschnitts-Rand auftretende größte Beanspruchung (Spannung) zu bestimmen. Das Widerstandsmoment ist unmittelbar aus dem Flächenträgheitsmoment zu ermitteln, indem...
Flächenträgheitsradius
Für geometrisch ähnliche Bauteile (z. B. Rechtecke mit gleichem Breiten/Höhen-Verhältnis) lässt sich auch der Flächenträgheitsradius mit der Dimension [Meter] definieren, mit dem man Körper vergleichen kann, die im Sinne des Flächenmomentes 2. Grades ähnlich sind:
Der Flächenträgheitsradius wird oft „Trägheitsradius“ genannt, was aber Verwechslungsgefahr zum Streumassenradius birgt. Außerdem ist der Flächenträgheitsradius im Schlankheitsgrad λ enthalten.
Flächensteife / Flächensteifigkeit
Im Flächenträgheitsradius ist die selten verwendete Flächensteife, auch Flächensteifigkeit genannt, enthalten. Die Flächensteife besitzt kein Formelzeichen und ist das Quadrat des Trägheitsradius bzw. der Quotient aus Flächenträgheitsmoment I und Querschnittsfläche A:
Sowohl Flächensteife als auch Flächenträgheitsradius sollten für eine gute Materialausnutzung möglichst groß sein. Dies führt jedoch zu immer größeren, dünnwandigeren Objekten, die dann zunehmend beulgefährdet sind.
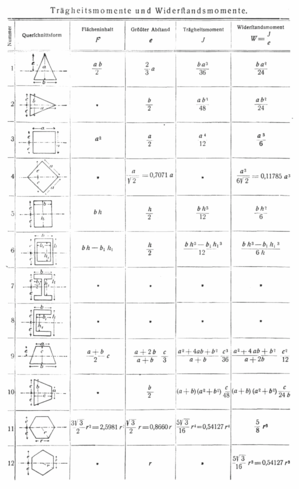
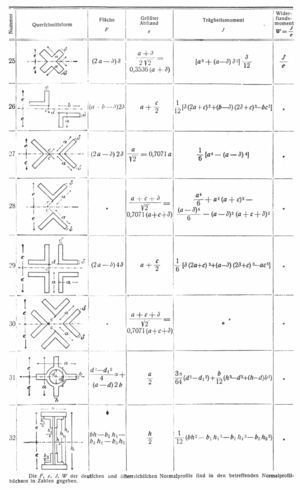
Beispiele

Das Polare Trägheitsmoment 2. Grades ist Ip = Iy + Iz, sofern der Bezugspunkt des polaren Flächenmomentes im Schnittpunkt der y- und z-Achse liegt.
Nr Fläche Axiales Flächenmoment
2. Grades um y- und z-Achse1: Rechteck 


Das Quadrat kann als Spezialfall des Rechtecks mit b = h berechnet werden 2:Dreieck 


Das Dreieck ist nur um die z-Achse symmetrisch 3:Kreisring 

Der Kreis kann als Spezialfall des Kreisrings mit r = 0 berechnet werden. 4:Ellipsenring 


Das Verhältnis  ist das Verhältnis der halben Achsen des Ellipsenringes und muss bei der Berechnung des polaren Flächenmomentes für die Ellipse am Innenrand gleich dem Verhältnis der Ellipse am Außenrand sein.
ist das Verhältnis der halben Achsen des Ellipsenringes und muss bei der Berechnung des polaren Flächenmomentes für die Ellipse am Innenrand gleich dem Verhältnis der Ellipse am Außenrand sein.
Die Ellipse kann als Spezialfall des Ellipsenringes mit a = b = 0 betrachtet werden.
5: Symmetrisches Trapez 


6: Regelmäßiges n-Eck 

Iy ist um alle Achsen gleich 7: Kastenprofil 

 -(nur für Profil 7; für Profil 8 und 9 gelten andere Formeln)
-(nur für Profil 7; für Profil 8 und 9 gelten andere Formeln)8: I-Träger (Doppel-T-Träger)
9: C-Profil
weitere Beispiele aus Lexikon der gesamten Technik:
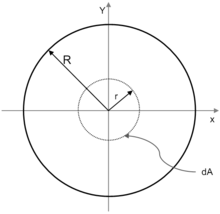
Beispiel gerechnet: Flächenträgheitsmoment eines Kreises mit Radius R


Für den Kreis gilt: Ix = Iy
Allgemein gilt: Ip = Ix + Iy
Daher ergibt sich das axiale Flächenträgheitsmoment eines Kreises zu:

Siehe auch
- Satz von Castigliano
- Die FEM-Simulation eignet sich für die Berechnung komplexer Geometrien
Wikimedia Foundation.