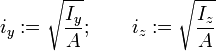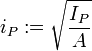- Flächendeviationsmoment
-
Das Flächenträgheitsmoment, auch als Flächenmoment 2. Grades bezeichnet, ist ein Maß für die Steifigkeit eines ebenen Querschnitts gegen Biegung.
Das Flächenträgheitsmoment ist nur abhängig von der Geometrie des Querschnittes. Im Gegensatz hierzu gibt der Elastizitätsmodul (bzw. der Schubmodul) Aufschluss über Materialeigenschaften.
Außerdem liefert das Flächenträgheitsmoment Aufschluss über die Neigung von Stäben zu knicken oder die Gefahr von Schalen zu beulen. Mit dem Flächenträgheitsmoment ist eine Spannungsverteilung infolge Biegung über einen Querschnitt errechenbar. Flächenträgheitsmoment und Elastizitätsmodul sind Konstanten in der Differentialgleichung der Biegelinie, welche das Verformungsverhalten von Stäben unter Last beschreibt (bei konstantem Stabquerschnitt).
Die etwas irreführende Bezeichnung „Flächenträgheitsmoment“ sollte nicht zur Verwechslung mit dem Massenträgheitsmoment führen, das die Trägheit gegenüber einer rotatorischen Beschleunigung charakterisiert. Vermutlich rührt die Bezeichnung von der Wesensgleichheit der zugrunde liegenden mathematischen Beziehungen her: Während das Massenträgheitsmoment als Integral über dem Produkt aus Abstandsquadrat und Massenelement gebildet wird, ergibt sich das Flächenträgheitsmoment als Integral über dem Produkt von Abstandsquadrat und Flächenelement.
Inhaltsverzeichnis
Grundlagen
Arten der Flächenträgheitsmomente
Grundsätzlich gibt es drei Arten Flächenträgheitsmomente:
- Das axiale Flächenträgheitsmoment ist ein Maß für den Widerstand eines Querschnitts gegen Biegung - siehe Balken (1) und (2) im Bild.
- Das biaxiale Flächenträgheitsmoment, auch als Flächendeviationsmoment, Deviationsmoment, Flächenzentrifugalmoment oder Zentrifugalmoment bezeichnet, ist von Bedeutung bei der Bestimmung der Deformation von unsymmetrischen Profilen und/oder bei unsymmetrischer Belastung beliebiger Profile - siehe Balken (3) im Bild.
- Das polare Flächenträgheitsmoment ist die Summe aus den axialen Flächenträgheitsmomenten in zwei senkrecht zueinander stehenden Richtungen. Oft wird irrtümlicherweise behauptet, das polare Flächenträgheitsmoment sei allgemein ein Maß für den Widerstand eines Querschnitts gegen Torsion - siehe Balken (4) im Bild. Das gilt aber in Wirklichkeit ausschließlich für Kreisquerschnitte und geschlossene Kreisringquerschnitte. Für alle anderen Fälle ist ein Torsionsträgheitsmoment definiert, für das sich nur in besonderen Fällen eine geschlossene Formel angeben lässt.
Flächenträgheitsmomente werden in der technischen Mechanik und den Ingenieurwissenschaften benötigt, um bei der Auslegung einer Konstruktion ihre Verformungen, Verdrehungen und vor allem die Stabilität von Bauteilen zu bestimmen.
Praktischer Bezug
Wenn ein Balken am Rande eingespannt und in einem gewissen Abstand mit einer Kraft belastet wird, dann biegt er sich durch. Die Balkenquerschnitte im Bild werden jeweils mit der gleichen Kraft im gleichen Abstand von einer Einspannstelle belastet.
Die mathematischen Formeln und die Erfahrungen zeigen nun, dass bei Belastung der schmalen Seite (1) eine geringere Durchbiegung zu erwarten ist, als bei Belastung der breiten Seite (2): s1 < s2; Wenn der Werkstoff isotrop ist (d. h. er ist homogen und hat keine Vorzugsrichtungen; Gegenbeispiel: Holz, das durch seine Fasern eine Vorzugsrichtung aufweist, längs derer es leicht spaltbar ist), dann kann offenbar nur die Form (Geometrie) des Körpers für die unterschiedliche Durchbiegung verantwortlich sein. Dieser geometrische Einfluss wird mathematisch durch das axiale Flächenmoment 2. Grades beschrieben. Er gilt innerhalb der Gültigkeitsgrenzen der Balkentheorie für alle Querschnitte mit gleichen Abmessungen und ist dann unabhängig von der Kraft und dem verwendeten Werkstoff.
Wenn ein Querschnitt nicht im Schubmittelpunkt belastet wird, verdrillt oder tordiert er. Der Verdrehwinkel wird bei gleicher Lagerung durch das polare Flächenträgheitsmoment beschrieben.
Anwendungsbereich
In der Praxis sind Flächenträgheitsmoment und Widerstandsmoment nur im Bereich der linearelastischen Verformungen (Hookscher Bereich) relevant. Für die gängigen Formen sind Flächenträgheitsmomente in der technischen Fachliteratur und teilweise auch in der mathematischen Literatur tabelliert.
Für die technische Betrachtung ist vor allem das Widerstandsmoment von Bedeutung. Es berücksichtigt neben dem Flächenträgheitsmoment auch den Abstand von der neutralen Faser zur Randfaser. Dadurch kann über den Vergleich mit der maximalen Spannung die zulässige Beanspruchung des Körpers berücksichtigt werden.
Berechnung der Flächenträgheitsmomente
Axiale Flächenträgheitsmomente
Die axialen Flächenträgheitsmomente lassen sich durch diese Gleichungen beschreiben:
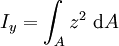 , Einheit: [m4]
, Einheit: [m4]
- z = senkrechter Abstand der y-Achse zum Element dA
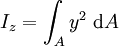 , Einheit: [m4]
, Einheit: [m4]
beide Größen können nur positive Werte annehmen.
Das biaxiale Flächenträgheitsmoment wird durch diese Gleichung beschrieben:
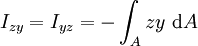 , Einheit: [m4]
, Einheit: [m4]
Diese auch Deviations- oder Zentrifugalmoment genannte Größe ist gleich Null, wenn entweder die y-Achse oder die z-Achse eine Symmetrieachse des Querschnitts ist. Die zugehörigen Flächenträgheitsmomente heißen dann Hauptträgheitsmomente, sie nehmen in diesem Falle extremale Werte an. Im Gegensatz zu den axialen und zum polaren Flächenträgheitsmoment kann diese Größe sowohl positive als auch negative Werte annehmen.
Das polare Flächenträgheitsmoment setzt sich aus den beiden Flächenträgheitsmomenten Iy und Iz zusammen:
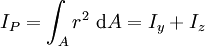 , Einheit: [m4]
, Einheit: [m4]
Alle hier genannten Flächenträgheitsmomente werden auf einen speziellen Punkt, nämlich den Flächenschwerpunkt bezogen. Für alle anderen Punkte können die Flächenträgheitsmomente mit dem Steinerschen Satz berechnet werden.
Satz von Steiner
Der Satz von Steiner besagt, dass sich das Flächenträgheitsmoment einer beliebigen Querschnittsfläche zusammensetzt aus den Flächenträgheitsmomenten im Hauptachsensystem der einzelnen Teilflächen und dem Produkt aus dem Quadrat des Abstandes z von Schwerachse-Gesamtfläche zu Schwerachse-Teilfläche und Teilfläche A. Ein Anwendungsbeispiel ist die I-Form. Die Flächenträgheitsmomente der drei rechteckigen Teilflächen, nämlich der beiden horizontalen Flansche und des vertikalen Stegs, lassen sich über die unten angegebenen Formeln bestimmen und für die vertikale z-Achse zu
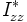 einfach summieren, denn alle Schwerpunkte der Teilflächen liegen auf der gemeinsamen Schwerachse z der Gesamtfläche. Das Flächenträgheitsmoment
einfach summieren, denn alle Schwerpunkte der Teilflächen liegen auf der gemeinsamen Schwerachse z der Gesamtfläche. Das Flächenträgheitsmoment 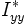 bezüglich der y-Achse setzt sich ebenfalls aus den drei Summanden plus dem Steiner'schen Anteil der beiden Flansche zusammen.
bezüglich der y-Achse setzt sich ebenfalls aus den drei Summanden plus dem Steiner'schen Anteil der beiden Flansche zusammen.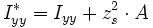 , Einheit: [m4]
, Einheit: [m4]
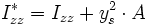 , Einheit: [m4]
, Einheit: [m4]
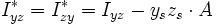 , Einheit: [m4]
, Einheit: [m4]
Hauptträgheitsmomente und verdrehte Trägheitsmomente
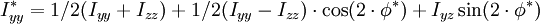 , Einheit: [m4]
, Einheit: [m4]
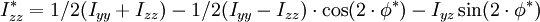 , Einheit: [m4]
, Einheit: [m4]
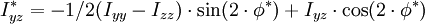 , Einheit: [m4]
, Einheit: [m4]
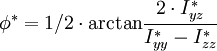 , Einheit: [°]
, Einheit: [°]
Mit Hilfe dieser Formeln kann man die zugehörigen Trägheitsmomente einer Fläche berechnen, wenn die Koordinatenachsen der Fläche um einen beliebigen Winkel φ verdreht werden. Neben dem Winkel müssen auch die Hauptträgheitsmomente Iyy und Izz gegeben sein. Da in früheren Jahren noch keine zuverlässigen Rechenmaschinen zur Verfügung standen, wurde ein grafisches Verfahren von Christian Otto Mohr angegeben. Der Mohrsche Trägheitskreis ist noch in vielen Lehrbüchern über die Technische Mechanik zu finden. Eine praktische Anwendung finden die verdrehten Flächenträgheitsmomente bei der Berechnung von Spannungen, wenn bei der Biegung das belastende Biegemoment nicht in die Richtung eines der beiden Hauptträgheitsmomente fällt.
Flächenträgheitsradien
Für geometrisch ähnliche Bauteile (z. B. Rechtecke mit gleichem Breiten/Höhen-Verhältnis) lässt sich auch der Flächenträgheitsradius mit der Dimension [Meter] definieren, mit dem man Körper vergleichen kann, die im Sinne des Flächenmomentes 2. Grades ähnlich sind:
Der Flächenträgheitsradius wird umgangssprachlich, aber inkorrekt oft nur „Trägheitsradius“ genannt und ist im Schlankheitsgrad λ enthalten.
Flächensteife/Flächensteifigkeit
Im Flächenträgheitsradius ist die selten verwendete Flächensteife, auch Flächensteifigkeit genannt enthalten. Die Flächensteife besitzt kein Formelzeichen und ist das Quadrat des Trägheitsradius bzw. der Quotient aus Flächenträgheitsmoment I und Querschnittsfläche A:
Sowohl Flächensteife als auch Flächenträgheitsradius sollten für eine gute Materialausnutzung möglichst groß sein. Dies führt jedoch zu immer größeren, dünnwandigeren Objekten, die dann zunehmend beulgefährdet sind.
Einheiten
Das Flächenträgheitsmoment wird üblicherweise in [m4] angegeben (SI-Einheiten). Im veralteten, aber in den USA noch gebräuchlichen Einheitensystem ist es normalerweise in [in4] notiert.
Beispiele
Das Polare Trägheitsmoment 2. Grades ist Ip = Iy + Iz, sofern der Bezugspunkt des polaren Flächenmomentes im Schnittpunkt der y- und z-Achse liegt.
Nr Fläche Axiales Flächenmoment
2. Grades um y- und z-Achse1: Rechteck 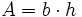
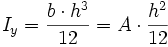
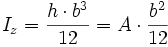
Das Quadrat kann als Spezialfall des Rechtecks mit b = h berechnet werden 2:Dreieck 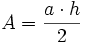
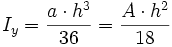
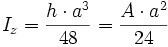
Das Dreieck ist nur um die z-Achse symmetrisch 3:Kreisring 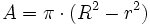
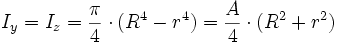
Der Kreis kann als Spezialfall des Kreisrings mit r = 0 berechnet werden. 4:Ellipsenring 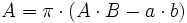
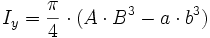
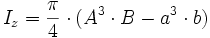
Das Verhältnis 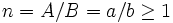 ist das Verhältnis der halben Achsen des Ellipsenringes und muss bei der Berechnung des polaren Flächenmomentes für die Ellipse am Innenrand gleich dem Verhältnis der Ellipse am Außenrand sein.
ist das Verhältnis der halben Achsen des Ellipsenringes und muss bei der Berechnung des polaren Flächenmomentes für die Ellipse am Innenrand gleich dem Verhältnis der Ellipse am Außenrand sein.
Die Ellipse kann als Spezialfall des Ellipsenringes mit a = b = 0 betrachtet werden.
5: Symmetrisches Trapez 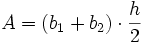
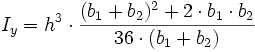
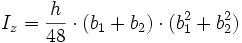
6: Regelmäßiges n-Eck 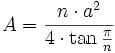
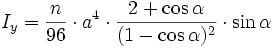
Iy ist um alle Achsen gleich 7: Kastenprofil 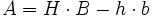
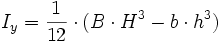
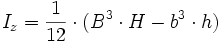 -(nur für Profil 7; für Profil 8 und 9 gelten andere Formeln)
-(nur für Profil 7; für Profil 8 und 9 gelten andere Formeln)8: I-Träger (Doppel-T-Träger)
9: C-Profil weitere Beispiele (eingescannt):
Beispiel gerechnet: Flächenträgheitsmoment eines Kreises mit Radius R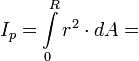 (Ansatz: polares Flächenträgheitsmoment)
(Ansatz: polares Flächenträgheitsmoment)
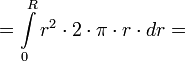 (Ersetzen von dA durch die Umfangsformel * dr)
(Ersetzen von dA durch die Umfangsformel * dr)
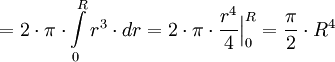
Für den Kreis gilt: Ix = Iy
Allgemein gilt: Ip = Ix + Iy
Daher ergibt sich das axiale Flächenträgheitsmoment eines Kreises zu:
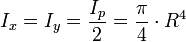
Siehe auch
- Flächenmoment, Trägheitsmoment, Satz von Castigliano
- Mit dem Widerstandsmoment lässt sich die Spannung in den Punkten mit dem größten Abstand zur neutralen Faser errechnen.
- Die FEM-Simulation eignet sich für die Berechnung komplexer Geometrien
- Technische Mechanik
- Steinerscher Satz
Wikimedia Foundation.