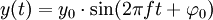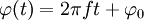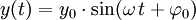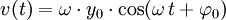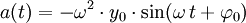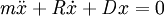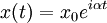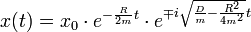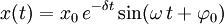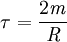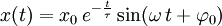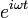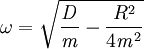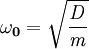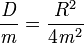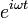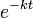Schwingungsdämpfung

Eine Schwingung (auch Oszillation) bezeichnet den Verlauf einer Zustandsänderung, wenn ein System auf Grund einer Störung aus dem Gleichgewicht gebracht und durch eine rücktreibende Kraft wieder in Richtung des Ausgangszustandes gezwungen wird.

Grundsätzlich basiert das Schwingen eines Systems auf der periodischen Energieumwandlung zwischen zwei Energieformen. Dabei durchläuft das System wiederholt nach einem festen Zeitintervall den Ausgangszustand.

Harmonische Schwingung

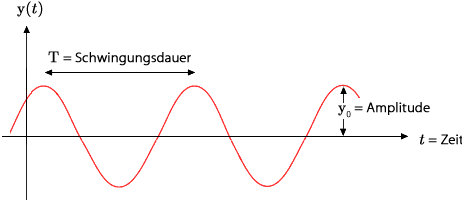
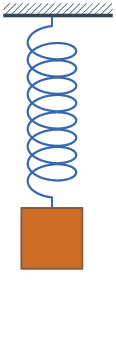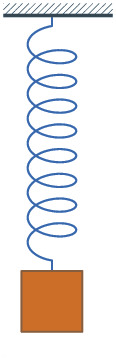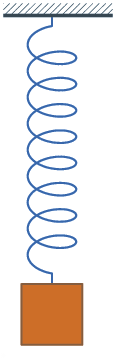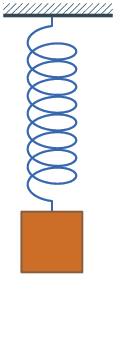
Darstellung des zeitlichen Verlaufs der Größe y(t) bei einer harmonischen Schwingung.

Im Rahmen der Anschauung wird hier die harmonische Schwingung als ein wichtiger Spezialfall betrachtet:

Die Grafik auf der rechten Seite zeigt eine ungedämpfte harmonische Schwingung mit der Auslenkung y(t), der Amplitude y₀ und der Periodendauer T.

Die Auslenkung y(t) zu einem Zeitpunkt t gibt den momentanen, die Amplitude den maximal möglichen Wert der Größe y an. Die Periodendauer oder die Schwingungsdauer ist die Zeit, die verstreicht, während ein schwingungsfähiges System genau eine Schwingungsperiode durchläuft, d. h. nach der es sich wieder im selben Schwingungszustand befindet. Der Kehrwert der Periodendauer T ist die Frequenz f, also: $f = {1 \over T} \quad$.
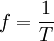Eine weitere Bezeichnungsform der Frequenz ist ν (sprich: "nü") und deren Einheit Hz (sprich: "Hertz").

Eine Schwingung ist harmonisch, wenn die Rückstellgröße (z. B. die rückstellende Kraft) proportional zur Auslenkung beispielsweise eines Pendels ist. Hierbei spricht man auch von einem linearen System, da die rückstellende Kraft sich linear mit der Auslenkung ändert: Verdoppelt sich diese, verdoppelt sich auch die rückstellende Kraft.

Eine solche Schwingung lässt sich beschreiben durch

$y(t)=y_0\cdot\sin(2\pi f t+\varphi_0) \,$

mit

y₀  = Amplitude und

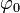$\varphi_0$  = Anfangsphase der Schwingung.

Mit

$\varphi (t) = 2 \pi f t+\varphi_0 \,$

wird die (Gesamt-)Phase bezeichnet, und f oder ν ist die Frequenz der Schwingung.

Das 2π-fache der Frequenz, 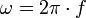$\omega = 2\pi \cdot f$, ist die Kreisfrequenz der Schwingung. Durch Verwendung der Kreisfrequenz ergibt sich eine kompaktere Schreibweise:

$y(t)=y_0\cdot\sin(\omega\,t+\varphi_0) \,$

Leitet man dieses nach der Zeit ab, so erhält man

$v(t)=\omega\cdot y_0\cdot \cos(\omega\,t+\varphi_0) \,$

mit

v(t) = Geschwindigkeit des schwingenden Körpers.

Nochmaliges Ableiten liefert:

$a(t)=-\omega^2\cdot y_0\cdot \sin(\omega\,t+\varphi_0) \,$

mit

a(t) = Beschleunigung des schwingenden Körpers.

Es gibt:

• gedämpfte und ungedämpfte Schwingungen,
• freie, erzwungene (oder fremderregte), selbsterregte und parametererregte Schwingungen,
• lineare und nichtlineare Schwingungen,
• Schwingungen mit einem Freiheitsgrad, mit endlich vielen Freiheitsgraden und mit unendlich vielen Freiheitsgraden (kontinuierliche Schwinger).

Alle diese Eigenschaften können kombiniert sein.

Gedämpfte Schwingung

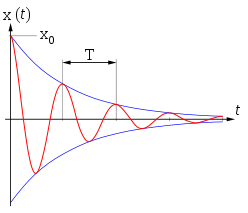
Darstellung des zeitlichen Verlaufs der Größe x(t) bei einer freien gedämpften Schwingung.

Tatsächliche physikalische Systeme sind immer gedämpft, da sie, z. B. durch Reibung, immer Energie an die Umgebung abgeben. Überlässt man ein solches System sich selbst (freie Schwingung), so führt dieses letztendlich zum „Stillstand“, wie aus dem zweiten Hauptsatz der Thermodynamik hervorgeht. Perpetua Mobilia sind also (siehe Energieerhaltungssatz) nicht möglich.

Stellt man das Kräftegleichgewicht einer freien gedämpften Schwingung auf, so findet man folgende allgemeine Bewegungsgleichung:

$\mathit{m} \ddot x + \mathit{R} \dot x + \mathit{D} x = 0 \,$

m: Masse
R: Reibungskoeffizient (nicht zu verwechseln mit der Abklingkonstante)
D: Federkonstante (Rückstellmoment) (Für Drehschwingungen ist m durch J (Trägheitsmoment) und x durch $\varphi$ (Auslenkungswinkel) zu ersetzen)

Mit Hilfe des komplexen Lösungsansatzes:

$x (t) = x_0 e^{i \alpha t} \,$

erhält man die allgemeine Lösung der Differentialgleichung:

$x (t) = x_0 \cdot e^{- \frac{\mathit{R}}{2\mathit{m}}t} \cdot e^{\mp i\sqrt{\frac{\mathit{D}}{\mathit{m}} - \frac{R^2}{4 \mathit{m}^2}}t} \,$

Überträgt man diese komplexe Lösung mit Hilfe der Eulerschen Formel in die reelle Ebene und setzt man 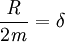$\frac{\mathit{R}}{2\mathit{m}} = \delta$, so ergibt sich folgende Schwingfunktion:

$x(t)=x_0\,e^{-\delta t}\sin(\omega\, t+ \varphi_0) \,$

Die in der reellwertigen Lösung enthaltenen Funktionen stellen zwei elementare Funktionen dar, die im Folgenden genauer erläutert werden sollen.

Wäre also die Dämpfungskonstante gleich Null, so würde die Amplitude niemals abnehmen. Die Schwingung würde sich ewig mit dem gleichen Ausschlag fortsetzen. Hier sieht man auch, dass die Dämpfungskonstante nicht zu hoch gewählt werden darf. Die Exponentenfunktion geht sonst sofort gegen null und es findet keine Schwingung im eigentlichen Sinne (Oszillation) statt, sondern das System kriecht sehr langsam in die Ruhelage zurück (Kriechfall). Die Grenze zwischen den beiden Fällen bildet der aperiodische Grenzfall.

Als Abklingdauer 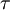$\mathbf{\tau}$ wird die Zeit bezeichnet, in der die Amplitude auf den e-ten Teil (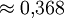$\approx{0{,}368}$) abgefallen ist. Wie deutlich aus der Gleichung der Amplitudenfunktion zu sehen, muss dafür τ gleich dem reziproken Wert des Exponenten der Funktion sein. Es ergibt sich die Abklingdauer:

$\tau=\frac{2\mathit{m}}{\mathit{R}}$

Häufig wird die gedämpfte Schwingung auch in einer Form angegeben, in der die Abklingdauer(auch Abklingzeit genannt) enthalten ist. Hierfür gilt dann:

$x(t)=x_0\,e^{-\frac{t}{\tau}}\sin(\omega\, t+\varphi_0) \,$

Das gleiche Symbol 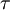$\mathbf{\tau}$ wird auch für die Relaxationszeit verwendet. Diese bezeichnet die Zeit, in der die Energie (nicht die Amplitude) des Systems auf den e-ten Teil (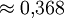$\approx{0{,}368}$) abgefallen ist. Da die Energie proportional zum Quadrat der Amplitude ist, entspricht die Relaxationszeit 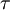$\mathbf{\tau}$ der Hälfte der Abklingdauer:

Relaxationszeit $\tau=\frac{\mathit{m}}{\mathit{R}} \,$

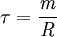
Grenzfälle

Den ungedämpften Anteil der allgemeinen Lösung kann man schreiben als

$\,e^{i \omega t} \,$

wobei der Faktor

$\omega = \sqrt{\frac{\mathit{D}}{\mathit{m}} - \frac{R^2}{4 \mathit{m}^2}}$

im Exponenten Kreisfrequenz genannt wird. Das Schwingungsverhalten hängt fundamental davon ab, welchen Wert ω hat:

• Wenn R hinreichend klein ist, ist die Schwingung nur schwach gedämpft und es gilt fast genau

$\mathbf{\omega_0} = \sqrt{\frac{\mathit{D}}{\mathit{m}}} \,$

• Wenn R größer wird, sinkt ω und die Schwingungsdauer T vergrößert sich.

• Wenn die Dämpfung so groß wird, dass

$\frac{\mathit{D}}{\mathit{m}} = \frac{R^2}{4 \mathit{m}^2}$

ist, wird ω = 0 und es gibt keine Schwingung mehr. In diesem Fall – dem aperiodischen Grenzfall – wird die Ruhelage in der kürzest möglichen Zeit erreicht.

• Für noch größere Werte von R wird der Wurzelinhalt negativ und ω imaginär. Der Faktor

$\,e^{i \omega t}$

wird wegen i² = -1 zu

$\,e^{- kt}$

und wirkt wie eine zusätzliche Dämpfung. Es gibt keine Schwingung mehr und die Ruhelage wird erst nach noch längerer Zeit als beim aperiodischen Grenzfall erreicht. Man spricht vom Kriechfall, der meist unerwünscht ist.

Freie oder erzwungene Schwingungen

Freie Schwingungen führt ein schwingfähiger Körper aus, der nach einer Störung/Auslenkung sich selbst überlassen, oszillierend (oder im Falle der kritischen bzw. überkritischen Dämpfung kriechend) in den Gleichgewichtszustand zurückkehrt; siehe oben. Die Frequenz der freien Schwingungen ist die Eigenfrequenz des Schwingers. Bei Schwingungen mit mehreren Freiheitsgraden gibt es entsprechend viele Eigenfrequenzen.

Erzwungene Schwingungen führt ein Schwinger aus, der durch zeitveränderliche äußere Einwirkung zum Schwingen angeregt (gezwungen) wird. Praktisch bedeutsam sind vor allem periodische Erregungen und darunter die harmonische, sinusförmige Erregung. Die Frequenz der periodischen Erregung wird als Erregerfrequenz bezeichnet. Es gibt auch mehrfrequente Erregungen. Aber auch Erregungen durch Zufallsprozesse (stochastische Schwingungen) werden untersucht.

Im Falle der harmonischen Erregung führt ein lineares System i. allg. zwei Schwingungen gleichzeitig aus:

• die freie Schwingung (mit der Eigenfrequenz bzw. mehreren Eigenfrequenzen), deren Größe von den Anfangsbedingungen abhängt und die durch die stets vorhandene Dämpfung während der Einschwingzeit abklingt und
• die erzwungene Schwingung im engeren Sinn mit der/den Erregerfrequenz(en), deren Amplitude(n) konstant ist (sind) und durch die Stärke der Erregung, das Verhältnis zwischen der Erregerfrequenz (oder einer der Erregerfrequenzen) und der Eigenfrequenz (oder einer der Eigenfrequenzen) sowie die Dämpfung des Schwingungssystems bestimmt wird. Diese wird durch die Vergrößerungsfunktion quantifiziert.

In der Technischen Mechanik sind die wichtigsten Erregungsmechanismen die Wegerregung, die Krafterregung und die Unwuchterregung.

Die Amplitude der erzwungenen Schwingung nimmt im Falle der Resonanz ein Maximum an. Bei fehlender Dämpfung und Gleichheit von (einer) Erregerfrequenz und (einer) Eigenfrequenz wird die Amplitude unendlich. Mit wachsendem Dämpfungswert verschiebt sich die Resonanzstelle geringfügig und die Resonanzamplitude nimmt ab.

Selbsterregte Schwingungen

Schwingungssysteme, bei denen die Energiezufuhr durch ein geeignetes Steuerelement und den Schwingungsvorgang selbst gesteuert wird, führen selbsterregte Schwingungen aus und werden Oszillator genannt. In den Differentialgleichungen wirkt sich diese Erscheinung so aus, dass der Dämpfungswert Null wird. Ein typisches Beispiel im Bereich der Mechanik sind die Schwingungen der Saiten einer Violine. Diese werden dadurch verursacht, dass die Haftreibung zwischen Bogen und Saite größer ist als die Gleitreibung und die Gleitreibung mit wachsender Differenzgeschwindigkeit noch abnimmt. Weitere Beispiele sind das Tönen von Gläsern durch Reiben des Randes und elektronische Taktgeber (Oszillatorschaltung).

Selbsterregte Schwingungen sind immer amplitudenbegrenzt, anderenfalls würden – wenn die Erregung zeitlich unbegrenzt wirkt – die Amplituden unbegrenzt anwachsen und zur Zerstörung des schwingenden Systems führen.

Parametererregte Schwingungen

Eine parametererregte Schwingung tritt dann auf, wenn sich Parameter des Schwingungssystems (Trägheitsgrößen, Dämpfungswerte oder Federkonstanten) periodisch ändern. So können z. B. bei Dampflokomotiven parametererregte Schwingungen zwischen den Treibachsen auftreten, weil sich die Steifheit der Verbindung durch die Kuppelstangen mit der Radstellung ändert.

Lineare und nichtlineare Schwingungen

Lineare Schwingungen sind dadurch gekennzeichnet, dass in den Differentialgleichungen des Schwingungssystems alle Abhängigkeiten von der schwingenden Größe und ihren zeitlichen Ableitungen linear sind. Bei nichtlinearen Schwingungen ist das nicht der Fall. Nichtlineare freie Schwingungen und nichtlineare erzwungene Schwingungen mit harmonischer Erregung sind nicht mehr streng sinusförmig, sondern enthalten höhere Harmonische. Von größerer praktischer Bedeutung ist jedoch, dass sich auch das Resonanzverhalten erzwungener Schwingungen ändert und die Amplituden selbsterregter Schwingungen beschränkt bleiben.

Schwingungen mit einem Freiheitsgrad oder mit endlich vielen Freiheitsgraden

Schwingungen mit einem Freiheitsgrad sind solche, die sich mit einer schwingenden Größe vollständig beschreiben lassen. Ein Beispiel dafür sind Schwingungen des ebenen Fadenpendels. Lässt man beim Pendel räumliche Bewegungen zu, so handelt es sich bereits um einen Schwinger mit zwei Freiheitsgraden. Wenn ein mechanisches Schwingungssystem mehrere Massen hat, deren Bewegung durch mindestens je eine Koordinate beschrieben werden muss, führt dieses ebenfalls Schwingungen mit mehreren Freiheitsgraden aus. Das gilt z. B. für die Torsionsschwingungen einer Kurbelwelle oder für die Horizontalschwingungen eines mehrgeschossigen Bauwerkes unter Erdbebeneinfluss.

Das Schwingungsverhalten eines Schwingers mit n Freiheitsgraden kann durch n Differentialgleichungen zweiter Ordnung beschrieben werden. Diese sind in der Regel über die schwingenden Größen, ihre ersten oder/und zweiten Ableitungen gekoppelt. Bei linearen Schwingungssystemen kann durch Einführung sog. Hauptkoordinaten mittels einer Koordinatentransformation eine Entkopplung der Differentialgleichungen bei den Koordinaten (Weggrößen) und ihren zweiten Ableitungen (Beschleunigungsgrößen) erreicht werden. In den meisten Fällen begeht man keinen großen Fehler, wenn man dann auch die Wirkung der ersten Ableitungen (Dämpfungsgrößen) als entkoppelt ansetzt. Aus den entkoppelten Differentialgleichungen bestimmt man die Eigenfrequenzen des Systems.

Nach der Lösung der Differentialgleichungen kann die Zeitabhängigkeit der ursprünglichen Koordinaten dann durch Rücktransformation ermittelt werden.

Bei nichtlinearen Schwingungssystemen ist eine Entkopplung der Differentialgleichungen in geschlossener Form nicht möglich. Es existieren jedoch Näherungsverfahren, die ausgehend von einer Linearisierung der Differentialgleichungen eine iterative Lösung ermöglichen.

Schwingungen mit unendlich vielen Freiheitsgraden

Unendlich viele Freiheitsgrade und damit unendlich viele Eigenfrequenzen haben Schwingungen der Kontinua, von praktischem Interesse sind in der Technik vor allem die Schwingungen von Saiten, Stäben, Platten und Schalen.

Weitere Beispiele

Typische Alltagsbeispiele für Schwingungen sind einfache Fadenpendel, die Schwingung des Quarzkristalls in der Quarzuhr, das Schaukeln auf einer Schaukel und vieles mehr. Auch die Atome in einem Kristallgitter schwingen um eine Gleichgewichtslage, und die Änderung der Jahreszeiten, die Drehung der Erde, der Herzschlag oder die Bewegung der Blätter im Wind sind genaugenommen Schwingungen. Hier gibt es überall zeitliche Änderungen von Zustandsgrößen.

Eine Schwingung des Fadenpendels beginnt damit, dass einem im Gleichgewicht befindlichen Körper eine Energie zugeführt wird (z. B. durch Auslenkung der Pendelmasse eines Fadenpendels, d. h. Zuführung von potentieller Energie). Im Prinzip kann dem Pendel auch eine Anfangsgeschwindigkeit (kinetische Energie) zugeführt werden.

Die sog. rücktreibende Kraft ist hier die Schwerkraft, die das Pendel nach unten zieht. Wieder in der anfänglichen Gleichgewichtslage angekommen, ist die gesamte zugeführte potentielle Energie in kinetische Energie umgewandelt, das Pendel bewegt sich durch die Gleichgewichtslage hindurch und erreicht im Idealfall nichtvorhandener Reibung wieder dieselbe Höhe. Gleichgewicht stellt sich dann ein, wenn das System seine potentielle Energie minimiert hat.

Das Fadenpendel führt nur bei sehr kleinen Amplituden, näherungsweise eine harmonische Schwingung, aus. Werden die Auslenkungen größer, so wird die rückstellende Kraft nicht proportional zur Auslenkung wachsen. Dieses ist also ein Beispiel für ein nichtlineares System, das sich für kleine Auslenkungen aber annähernd wie ein lineares System verhält.

Schwingungen können auch gleichzeitig von mehreren Kräften beeinflusst werden, oder ein Körper kann mehrere Schwingungen gleichzeitig, d. h. überlagert, ausführen (z. B. Schwebung). Man kann jede beliebige Bewegung eines Körpers im Raum in voneinander unabhängige Bewegungsrichtungen zerlegen. Das heißt, ein Körper kann in die drei Raumrichtungen (sie stehen senkrecht zueinander) bewegt werden, und sich noch um drei gedachte Bewegungsachsen (sie stehen ebenfalls aufeinander senkrecht) drehen. Somit hat jeder starre Körper im Raum sechs Bewegungsfreiheitsgrade. Die entstehenden Überlagerungsfiguren werden Lissajous-Schleifen genannt.

Bei Elektronenröhren wird häufig Mikrofonie beobachtet. Sie entsteht durch von außen auf die Bauteile einwirkende störende mechanische Schwingungen etwa durch nah dabeistehende Lautsprecher.

Als Regenerativeffekt wird ein Begriff aus der Fertigungstechnik bezeichnet. Er beschreibt die Schwingungen während des Fertigungsvorganges, die innerhalb einer Maschine auftreten.

Siehe auch

• Spektrale Beschleunigungsdichte
• Harmonograph
• Schwingungen in rotierenden Strukturen