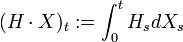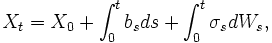Semimartingale

Als Semimartingale werden in der Stochastik bestimmte Prozesse bezeichnet, die insbesondere für die Definition eines allgemeinen stochastischen Integrals von Bedeutung sind. Die Klasse der Semimartingale umfasst viele bekannte stochastische Prozesse wie den Wiener-Prozess (Brownsche Bewegung) oder den Poisson-Prozess.

Definition

Gegeben sei ein Wahrscheinlichkeitsraum 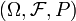$(\Omega, \mathcal F, P)$ mit zugehöriger Filtration 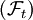$(\mathcal F_t)$. Dabei wird angenommen, dass die Filtration vollständig ist, es sollen also alle P-Nullmengen bereits 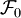$\mathcal F_0$-messbar sein.

Ein Semimartingal ist dann ein stochastischer Prozess 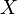$X\;$ mit Werten in 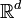$\mathbb R^d$, der an die gegebene Filtration adaptiert und rechtsseitig stetig mit linksseitig existierenden Grenzwerten ist und für den eine Darstellung

X = X₀ + M + A,

existiert, wobei 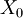$\;X_0$ fast sicher endlich und 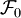$\mathcal F_0$-messbar, 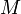$M\;$ ein lokales Martingal und 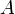$A\;$ ein Prozess von endlicher Variation ist. Diese Zerlegung ist im allgemeinen nicht eindeutig.

Eigenschaften

Stochastische Integration

Wie bereits in der Einleitung angedeutet, lassen sich mit Hilfe von Semimartingalen allgemeine stochastische Integrale konstruieren. Semimartingale stellen die größte Klasse von Integratoren dar, für die ein Integral der Form

$(H \cdot X)_t := \int_{0}^{t} H_s dX_s$

sinnvoll definiert werden kann. 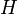$H\;$ stammt in diesem Fall aus der Menge aller lokal beschränkter vorhersagbarer Prozesse.

Stabilität unter Transformationen

Die Klasse der Semimartingale ist unter vielen Operationen stabil. Nicht nur ist jedes gestoppte Semimartingal offensichtlich wieder ein Semimartingal, auch unter Lokalisierung, einem "Wechsel der Zeit" oder einem Übergang zu einem neuen absolut stetigen Maß bleiben Semimartingale erhalten.

Beispiele

Martingale

Jedes Martingal ist trivialerweise ein Semimartingal, da jedes Martingal selbst ein lokales Martingal ist.

Sprungprozesse

Viele Sprungprozesse wie verallgemeinerte Poisson-Prozesse sind Semimartingale, da sie von beschränkter Variation sind.

Ito-Diffusionen

In der Finanzmathematik spielen Ito-Diffusionen eine zentrale Rolle. Diese sind im wesentlichen darstellbar als

$X_t = X_0 + \int_{0}^{t} b_s ds +\int_{0}^{t} \sigma_s dW_s,$

wobei der letzte Term ein Ito-Integral mit Volatilitätsfunktion σ_s bezeichnet.

Literatur

• Jean Jacod, Albert N. Shiryaev: Limit Theorems for Stochastic Processes. 2. Auflage. Springer, Berlin 2002, ISBN 3540439323. 
• Philip Protter: Stochastic Integration and Differential Equations. 2. Auflage. Springer, Berlin 2003, ISBN 3540003134.