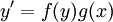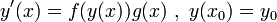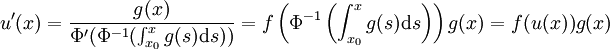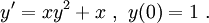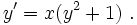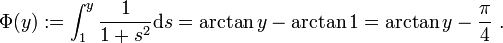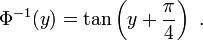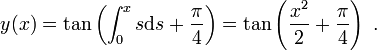- Separierbare Differentialgleichung
-
Die Methode der Trennung der Veränderlichen (auch Trennung der Variablen, Separationsmethode oder Separation der Variablen) ist ein Verfahren aus der Theorie der gewöhnlichen Differentialgleichungen um Differentialgleichungen erster Ordnung der Gestalt
zu lösen.
Der Begriff „Trennung der Veränderlichen“ geht auf Johann Bernoulli zurück, der ihn 1694 in einem Brief an Gottfried Wilhelm Leibniz verwendete.[1]
Inhaltsverzeichnis
Lösung des Anfangswertproblems
Wir untersuchen das Anfangswertproblem
für stetige (reelle) Funktionen f und g. Falls f(y0) = 0, so wird dieses Anfangswertproblem durch die konstante Funktion
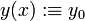 gelöst.
gelöst.Formulierung des Satzes
Es seien
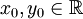 mit
mit 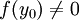 . Dann gilt:
. Dann gilt:- Es gibt ein y0 umfassendes offenes Intervall
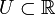 mit
mit 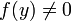 für alle
für alle 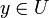 . Dann ist die Abbildung
. Dann ist die Abbildung 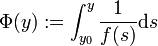 auf U wohldefiniert und streng monoton.
auf U wohldefiniert und streng monoton.
- Weiter gibt es ein x0 umfassendes offenes Intervall
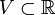 , so dass die Abbildung
, so dass die Abbildung 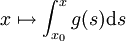 für alle
für alle 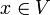 Werte in Φ(U) hat.
Werte in Φ(U) hat.
- Seien U und V wie oben. Dann ist
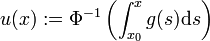 eine Lösung des Anfangswertproblems
eine Lösung des Anfangswertproblems
-
- auf V. u erfüllt also die implizite Gleichung
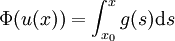 .
.
Beweis
Da
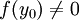 und f stetig, gibt es ein y0 umfassendes offenes Intervall U, so dass
und f stetig, gibt es ein y0 umfassendes offenes Intervall U, so dass 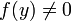 für alle
für alle 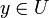 . Insbesondere hat f auf U dasselbe Vorzeichen, so dass
. Insbesondere hat f auf U dasselbe Vorzeichen, so dass 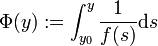 auf U wohldefiniert und streng monoton ist. Φ(U) ist ein 0 umfassendes offenes Intervall. Also gibt es ein x0 umfassendes offenes Intervall
auf U wohldefiniert und streng monoton ist. Φ(U) ist ein 0 umfassendes offenes Intervall. Also gibt es ein x0 umfassendes offenes Intervall 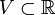 , so dass
, so dass 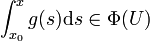 für alle
für alle 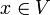 gilt.
gilt.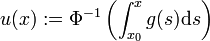 ist auf V wohldefiniert, und wegen
ist auf V wohldefiniert, und wegen 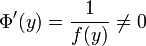 für alle
für alle 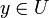 gilt
giltauf V. Bei der Ableitung u'(x) wurden die Kettenregel und die Umkehrregel genutzt. Natürlich ist g(x0) = y0.

Beispiel
Gesucht sei die Lösung y des Anfangswertproblems
Hierbei handelt es sich um eine Differentialgleichung mit getrennten Variablen:
Setze also
Die Umkehrfunktion lautet
Also ist die Lösung des Anfangswertproblems gegeben durch

Quellen
- ↑ Harro Heuser: Gewöhnliche Differentialgleichungen. Einführung in Lehre und Gebrauch. 2. Auflage. Teubner, Stuttgart 1991, ISBN 3-519-12227-8, S. 128
Wikimedia Foundation.