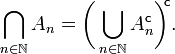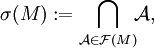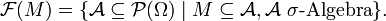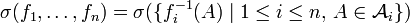- Sigmakörper
-
Eine σ-Algebra (auch σ-Mengenalgebra, Sigmakörper oder Borelscher Mengenkörper) ist ein Grundbegriff der Maßtheorie. Als solcher wird sie auch in der Stochastik häufig verwendet. Eine σ-Algebra ist eine mengentheoretische Struktur, sie bezeichnet ein Mengensystem auf einer festen Grundmenge, das die Grundmenge enthält und abgeschlossen ist bezüglich der Komplementbildung und abzählbaren Vereinigungen.
Inhaltsverzeichnis
Definition
Als σ-Algebra bezeichnet man in der Mathematik ein Mengensystem (in der Stochastik das Ereignissystem)
 mit
mit 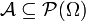 , also eine Menge
, also eine Menge  von Teilmengen der Grundmenge (in der Stochastik: Ergebnismenge) Ω, welche die folgenden Bedingungen erfüllt:
von Teilmengen der Grundmenge (in der Stochastik: Ergebnismenge) Ω, welche die folgenden Bedingungen erfüllt: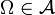 (Die Grundmenge Ω ist in
(Die Grundmenge Ω ist in  enthalten.)
enthalten.)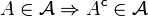 (Wenn
(Wenn  eine Teilmenge A von Ω enthält, dann auch deren Komplement
eine Teilmenge A von Ω enthält, dann auch deren Komplement 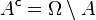 .)
.)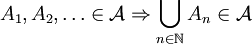 . (Wenn für jede natürliche Zahl n die Menge An in
. (Wenn für jede natürliche Zahl n die Menge An in  ist, so ist auch die abzählbare Vereinigung aller An in
ist, so ist auch die abzählbare Vereinigung aller An in  .)
.)
Erläuterungen
- Aus den Bedingungen 1 und 2 folgt, dass
 immer das Komplement von Ω, also die leere Menge enthält. Aufgrund der Eigenschaft 2 kann man in Eigenschaft 1 alternativ zu
immer das Komplement von Ω, also die leere Menge enthält. Aufgrund der Eigenschaft 2 kann man in Eigenschaft 1 alternativ zu 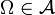 auch
auch 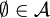 fordern.
fordern. - Wählt man in Bedingung 3 die Mengen
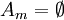 für alle m > n, so folgt, dass die endliche Vereinigungsmenge
für alle m > n, so folgt, dass die endliche Vereinigungsmenge 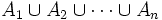 in
in  enthalten ist.
enthalten ist. - Ist
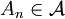 für jede natürliche Zahl n, so folgt aus den De Morganschen Gesetzen und den Bedingungen 2 und 3, dass auch die Schnittmenge in
für jede natürliche Zahl n, so folgt aus den De Morganschen Gesetzen und den Bedingungen 2 und 3, dass auch die Schnittmenge in  ist, weil
ist, weil
- Wählt man Am = Ω für alle m > n, so folgt, dass der Durchschnitt
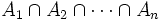 von endlich vielen Mengen in
von endlich vielen Mengen in  enthalten ist. Eine σ-Algebra ist also abgeschlossen gegenüber endlichen und abzählbar unendlichen Durchschnitten.
enthalten ist. Eine σ-Algebra ist also abgeschlossen gegenüber endlichen und abzählbar unendlichen Durchschnitten. - Sind A und B aus
 , so ist auch
, so ist auch 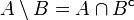 in
in  . Also ist
. Also ist  abgeschlossen gegen Mengendifferenz.
abgeschlossen gegen Mengendifferenz. - Ferner ist jede σ-Algebra insbesondere auch ein Dynkin-System.
Beispiele
- Für jede beliebige Menge Ω ist
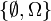 die kleinste und die Potenzmenge
die kleinste und die Potenzmenge 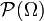 die größte mögliche σ-Algebra.
die größte mögliche σ-Algebra. - Für jede beliebige Menge Ω und Teilmenge
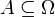 ist
ist 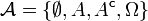 die kleinste σ-Algebra, die A enthält.
die kleinste σ-Algebra, die A enthält. - Für jeden topologischen Raum Ω existiert die σ-Algebra der Borelschen Teilmengen von Ω, die unter anderem alle offenen und abgeschlossenen Teilmengen von Ω enthält.
- Die σ-Algebra der Borelschen Teilmengen der reellen Zahlen enthält unter anderem alle Intervalle.
- Über einer Grundmenge Ω ist das Mengensystem
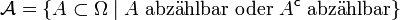 eine σ-Algebra. Ist hierbei Ω überabzählbar, so ist eine Funktion
eine σ-Algebra. Ist hierbei Ω überabzählbar, so ist eine Funktion 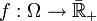 genau dann messbar, wenn sie auf dem Komplement einer abzählbaren Menge konstant ist.
genau dann messbar, wenn sie auf dem Komplement einer abzählbaren Menge konstant ist.
Bedeutung
σ-Algebren bilden den Ausgangspunkt für die Definition des Maßraums und des Wahrscheinlichkeitsraums. Das Banach-Tarski-Paradoxon demonstriert, dass auf überabzählbaren Mengen die durch die Potenzmenge gebildete σ-Algebra als Grundlage für die Volumenbestimmung zu groß sein kann und die Betrachtung anderer σ-Algebren mathematisch notwendig ist. In der Theorie der stochastischen Prozesse, insbesondere in der stochastischen Finanzmathematik, wird die bis zu einem Zeitpunkt prinzipiell beobachtbare Information durch eine σ-Algebra beschrieben, was zum Begriff der Filtrierung, also einer zeitlich aufsteigenden Familie von σ-Algebren führt. Filtrierungen sind essentiell für die allgemeine Theorie der stochastischen Integration; Integranden (also finanzmathematische Handelsstrategien) dürfen zu einer Zeit t nur von den Informationen bis (ausschließlich) t abhängen; insbesondere dürfen sie nicht „in die Zukunft schauen“.
σ-Operator
1. Für eine beliebige Teilmenge M der Potenzmenge
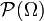 ist der σ-Operator definiert als
ist der σ-Operator definiert alswobei
Da die Schnittmenge einer Familie von σ-Algebren (über derselben Grundmenge Ω) wieder eine σ-Algebra ist, ist σ(M) somit die kleinste σ-Algebra, die M umfasst.
Der σ-Operator erfüllt die fundamentalen Eigenschaften eines Hüllenoperators:
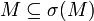 , also der σ-Operator ist extensiv.
, also der σ-Operator ist extensiv.- Gilt
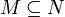 , so ist auch
, so ist auch 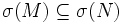 (Monotonie bzw. Isotonie).
(Monotonie bzw. Isotonie). - Es ist σ(σ(M)) = σ(M) (Idempotenz).
σ(M) wird als die von M erzeugte σ-Algebra bezeichnet, M heißt Erzeuger dieser σ-Algebra.
2. Sind
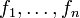 Funktionen von Ω in Messräume
Funktionen von Ω in Messräume 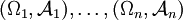 , so ist
, so istdie kleinste σ-Algebra über Ω, bezüglich derer die fi messbar sind. Sie wird als die von
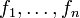 erzeugte σ-Algebra bezeichnet. Entsprechendes gilt für beliebige Indexmengen I statt
erzeugte σ-Algebra bezeichnet. Entsprechendes gilt für beliebige Indexmengen I statt 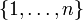 .
.Spur-σ-Algebra
Für
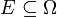 wird das Mengensystem
wird das Mengensystem 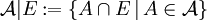 als Spur von
als Spur von  in E bzw. Spur-σ-Algebra von
in E bzw. Spur-σ-Algebra von  über E bezeichnet. Man kann zeigen, dass die Spur von
über E bezeichnet. Man kann zeigen, dass die Spur von  in E wieder eine σ-Algebra (aber mit der Grundmenge E) ist, was den Namen "Spur-σ-Algebra" rechtfertigt.
in E wieder eine σ-Algebra (aber mit der Grundmenge E) ist, was den Namen "Spur-σ-Algebra" rechtfertigt.Literatur
- Heinz Bauer: Maß- und Integrationstheorie. Walter de Gruyter, Berlin–New York 1992. ISBN 3-11-013626-0
- Jürgen Elstrodt: Maß- und Integrationstheorie. ISBN 3-540-65420-8
- Ernst Henze: Einführung in die Maßtheorie. ISBN 3-411-03102-6
Siehe auch
Wikimedia Foundation.