Solow-Swan-Modell

Das Solow-Modell ist ein volkswirtschaftliches Modell zur Erklärung des langfristigen Wachstums einer Volkswirtschaft. Das Modell wurde von Robert Merton Solow (1956) und Trevor Swan (1956) entwickelt. Es ist ein wichtiger Bestandteil der neoklassischen Wachstumstheorie und entwickelte sich aus der Kritik heraus, dass die Determinanten des Wirtschaftswachstums z. B. im Harrod-Domar-Modell nicht betrachtet wurden.

Die zentrale Aussage des Solow-Modells ist, dass für dauerhaftes Wirtschaftswachstum langfristig nur technischer Fortschritt von Bedeutung ist. Wachstumspolitik kann folglich auf lange Sicht nur erfolgreich sein, wenn sie den technischen Fortschritt begünstigt.

Herleitung des Solow-Modells

Das Solow-Modell erklärt Wachstum als Folge aus Arbeits-, Kapital- und Technologie-Einsatz in einer Volkswirtschaft. Das Modell liefert jedoch nur eine Erklärung für ein endogenes Anpassungswachstum hin zu einem langfristigen Gleichgewicht. In diesem Gleichgewicht wird die Kapitalintensität, also der Kapitalstock pro Kopf konstant gehalten. Dies ist dann der Fall, wenn die Verringerung des Kapitalstocks pro Kopf auf Grund von Abschreibungen und Bevölkerungswachstum genau durch neue Investitionen in den Kapitalstock ausgeglichen werden. Die Annahme ist auf die Realität übertragbar, wenn man sich vorstellt, dass in diesem Gleichgewicht die ausrangierten Maschinen gerade durch neue ersetzt werden. Daraus ergibt sich, dass die Volkswirtschaft wächst, wenn die Investitionen größer sind als die Abschreibungen und dass sie schrumpft, wenn die Investitionen geringer sind als die Abschreibungen.

Weitere Annahmen werden insofern getroffen, dass der Pro-Kopf-Kapitalstock bei einem steigenden Bevölkerungswachstum sinkt, da das gesamte vorhandene Einkommen auf mehr Köpfe verteilt werden muss. Außerdem wird eine Rate des technischen Fortschritts in der Volkswirtschaft angegeben, die den vorhandenen Kapitalstock veralten lässt.

Das Modell kommt zu dem Ergebnis, dass das Wachstum einer jeden Volkswirtschaft gegen einen langfristig gegebenen Punkt (Steady State) konvergiert, der durch die Investitionen in der Volkswirtschaft, die konstante Abschreibungsrate, das Bevölkerungswachstum und die Rate des technologischen Fortschritts bestimmt wird. Damit die Volkswirtschaft langfristig wächst, muss technologischer Fortschritt vorhanden sein.

Mathematische Beschreibung des Solow-Modells

Mathematisch wird die Berechnung des volkswirtschaftlichen Gleichgewichts wie folgt beschrieben:

Y = Produktion

L = Arbeit

K = Kapital

A = Technischer Fortschritt

α = Produktionselastizität des Kapitals

s = Sparquote

δ = Abschreibungen

g_X = Wachstumsrate des Faktors X (X kann also durch Y, L, K oder A ersetzt werden)

Die gesamtwirtschaftliche Produktionsfunktion, auf der das Solow-Modell basiert, ist eine Cobb-Douglas-Funktion mit technischem Fortschritt. Sie sieht wie folgt aus:

$Y = A \cdot F(K, L) = AK^{\alpha}L^{1-\alpha}$,

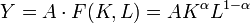wobei 0 < α < 1.

Diese Produktionsfunktion besitzt konstante Skalenerträge (Homogenitätsgrad =  1) bezüglich der Produktionsfaktoren Kapital und Arbeit. Das heißt, multipliziert man die Produktionsfaktoren mit einem festen Faktor, so vervielfacht sich auch die Produktion um genau diesen Faktor.

Die Gleichung für das Solow-Modell wird durch eine Reihe von Umformungen und Annahmen erreicht. So wird die Produktionsfunktion als Pro-Kopf-Einkommen umgeschrieben, indem man die Gleichung durch L dividiert. Dies stellt nur eine Näherung dar, da L nicht der Gesamtbevölkerung entspricht. Da aber letztendlich nur Aussagen bezüglich Wachstumsgrößen getroffen werden, ist diese Näherung zulässig unter der plausiblen Annahme, dass L mit derselben Rate wächst wie die Gesamtbevölkerung.

Zur Unterscheidung von den gesamtwirtschaftlichen Größen werden die Pro-Kopf-Größen mit Kleinbuchstaben dargestellt. Die Produktionsfunktion wird damit wie folgt umgeformt:

$\frac{Y}{L} = \frac{A \cdot K^{\alpha}L^{1-\alpha}}{L} = \frac{A \cdot K^{\alpha}L^{1-\alpha}}{L^{\alpha}L^{1-\alpha}} = A \cdot {(\frac{K}{L})}^{\alpha} \cdot {(\frac{L}{L})}^{1-\alpha} = A \cdot {(\frac{K}{L})}^{\alpha} = A \cdot k^{\alpha} \quad \Leftrightarrow \quad y = A \cdot k^{\alpha} = A \cdot f(k)$

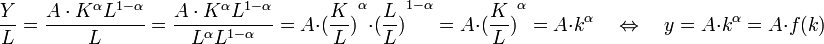
Es wird angenommen, dass es eine Sparquote s gibt, die den Anteil des (Pro-Kopf-)Einkommens beschreibt, der gespart und damit in die Erhöhung des (Pro-Kopf-)Kapitalstocks investiert wird. δ bezeichnet die Abschreibungsrate, die den Verfall des vorhandenen (Pro-Kopf-)Kapitalstocks erfasst. Das Bevölkerungswachstum wird mit g_L bezeichnet.

Im langfristigen Gleichgewicht - dem „Steady state"-Niveau der Volkswirtschaft - muss gelten, dass die Investitionen in den Kapitalstock gleich den Abschreibungen (inkl. Bevölkerungswachstum) des Kapitalstocks entsprechen (siehe auch Harrod-Domar-Modell):

$s \cdot y = (\delta + g_L) \cdot k \quad \Leftrightarrow \quad s \cdot A \cdot f(k) = (\delta + g_L) \cdot k$

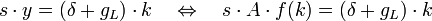
Dabei ist zu beachten, dass das Solow-Modell eine Geschlossene Volkswirtschaft beschreibt, d. h. es werden keine Wirtschaftsbeziehungen mit dem Ausland im Modell berücksichtigt.

Goldene Regel der Kapitalakkumulation

Die Goldene Regel der Akkumulation beschreibt diejenige Sparquote in einer Volkswirtschaft, durch die der Konsum maximiert wird.

Der Konsum ist der Anteil der Produktion, der nicht gespart wird. Bezeichne c die Konsumquote, so gilt:

$c \cdot y = (1-s) \cdot y = (1-s) \cdot A f(k) = A f(k) - s A f(k)$

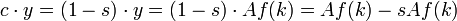
Wie oben gesehen, muss also im langfristigen Gleichgewicht (Steady State) gelten:

$c \cdot y = A \cdot f(k) - (\delta + g_L) \cdot k$

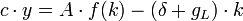
Um nun die Sparquote zu finden, die den Konsum maximiert, ist es einfacher, zunächst den Steady-State-Kapitalstock zu bestimmen, der den Konsum maximiert, und damit die optimale Sparquote zu berechnen. Dies ist möglich, da zwischen Steady-State-Kapitalstock und Sparquote ein eindeutiger Zusammenhang besteht.

Um den konsummaximierenden Kapitalstock zu finden, wird die letzte Gleichung für die Bedingung Erster Ordnung nach k abgeleitet. Damit erhält man für das Optimum:

$A \cdot f'(k^*) - (\delta + g_L) = 0 \quad \Leftrightarrow \quad Af'(k^*) = \delta + g_L$

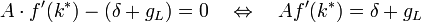
Legt man wie oben die Cobb-Douglas-Produktionsfunktion zu Grunde, so dass gilt: f(k) = k^α mit 0 < α < 1, so erkennt man, dass auch die Bedingung Zweiter Ordnung (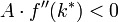$A \cdot f''(k^*) &amp;lt; 0$) immer erfüllt ist.

Damit stellt k ^* den konsummaximierenden Steady-State-Kapitalstock dar.

Weiterhin ist bereits bekannt, dass im Steady State immer gilt:

$s \cdot A \cdot f(k) = (\delta + g_L) \cdot k \quad \Leftrightarrow \quad \delta + g_L = \frac{s \cdot A \cdot f(k)}{k}$

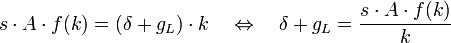
Eingesetzt in die obige Bedingung erster Ordnung erhält man für die optimale (konsummaximierende) Sparquote s ^* :

$Af'(k) = \frac{s^* \cdot A \cdot f(k)}{k} \quad \Leftrightarrow \quad s^* = \frac{k \cdot Af'(k^*)}{A \cdot f(k^*)}$

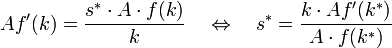
Mit f(k) = k^α ergibt sich:

s ^* = α

Bei dieser Sparquote wird der Konsum im langfristigen Gleichgewicht maximiert.

Entwicklung der Theorie

Robert Solow konnte 1957 die empirische Evidenz des Solow-Modells anhand von Wachstumsdaten der USA nachweisen. Dazu benutzte er methodisch die sog. Solow-Residuen, auch als totale Faktorproduktivität bezeichnet, um den Anteil des technologischen Fortschritts aus dem Gesamtwachstum eines Jahres auszumachen. Es stellte sich heraus, dass der größte Anteil des jährlichen Wachstums nicht auf Arbeit- oder Kapitalfaktoren sondern auf den technologischen Fortschritt zurückzuführen ist.

Kritik an der Theorie und Weiterentwicklung

Das Solow-Modell wird seit den 80er Jahren, vor allen von den Verfechtern des endogenen Wachstums, kritisiert. Im Zentrum der Kritik stand die Konvergenz des Wachstums einer Volkswirtschaft im Solow-Modell. Dies bedeutet, dass ärmere Volkswirtschaften langfristig zu den wohlhabenderen aufschließen, da sie ohne größere Mühen schneller wachsen können. Diese Konvergenz konnte aber nicht in allen Volkswirtschaften nachgewiesen werden. Zu den Fällen konvergierenden Wachstums gehören vor allem die Marktwirtschaften aus Europa, Nordamerika und verschiedene Staaten in Ost- und Südostasien (vgl. auch Tigerstaaten). Zudem seien die berechneten Konvergenzgeschwindigkeiten zu hoch und das Modell liefere nur brauchbare Ergebnisse für das 20. Jahrhundert.

Als weiterer Kritikpunkt wird genannt, dass im Solow-Modell der technologische Fortschritt einziger Faktor langfristigen Wachstums ist, das Modell aber nicht erklärt wie dieser zustande kommt. Technologischer Fortschritt wird als exogen gegeben angesehen und daher nicht durch das Modell erklärt.

Die Kritik am exogenen technologischen Fortschritt greift die Endogene Wachstumstheorie auf. Um die weiteren oben genannten Kritikpunkte am Solow-Modell auszuräumen haben Mankiw, Romer und Weil 1992 eine überarbeitete Fassung des Modells veröffentlicht, die den Faktor Humankapital und Bildung mit in die Berechnung des Wachstums einbezieht. Die Probleme fehlender Konvergenz und übertriebener Konvergenzgeschwindigkeiten werden dadurch erklärt.

Schließlich wurde das Solow-Modell als Ein-Gut-Parabel kritisiert. Einige Ergebnisse des Modells lassen sich nicht verallgemeinern, wenn man von der (unausgesprochenen) Annahme einer Volkswirtschaft, die nur ein Gut „Y" produziert, das dann als Konsum- („C") oder Investitionsgut („I") eingesetzt werden kann, zu der wirklichkeitsnäheren Annahme einer Volkswirtschaft, in der „Waren mittels Waren" hergestellt werden (Piero Sraffa), übergeht.

Als die entscheidende globale Fehlannahme muss wohl die völlige Ausblendung der Unmöglichkeit eines dauerhaften, ressourcenverbrauchenden Wachstums in einer finiten Welt angesehen werden. Spätestens mit dem Schrumpfen bzw. der schwierigeren Erreichbarkeit wichtiger Rohstoff- und bes. der Energieträgervorräte - etwa des Erdöls (vgl. Peak Oil) oder der Kohle - wird auch das Solow-Modell an die Grenzen seiner Erklärfähigkeit gelangen.

Siehe auch

• Growth Accounting

Weblinks

• Java-Rechenservice Solow-Modell
• Java Applet zur Darstellung des Solow-Modell

Literatur

• Robert Merton Solow: „A Contribution to the Theory of Economic Growth“ in Quarterly Journal of Economics Band 70, 1956, S. 65–94.

→ deutsche Übersetzung: König, H. (Hrsg.): „Ein Beitrag zur Theorie des wirtschaftlichen Wachstums“ in Wachstum und Entwicklung der Wirtschaft, Köln, 1968, S. 67–96.

• Lucas Bretschger: „Wachstumstheorie“, 3. überarbeitete und erweiterte Auflage, Oldenburg, 2004, Kapitel 3 Seite 25–40, ISBN 3-486-20003-8.